Question Number 88567 by jagoll last updated on 11/Apr/20
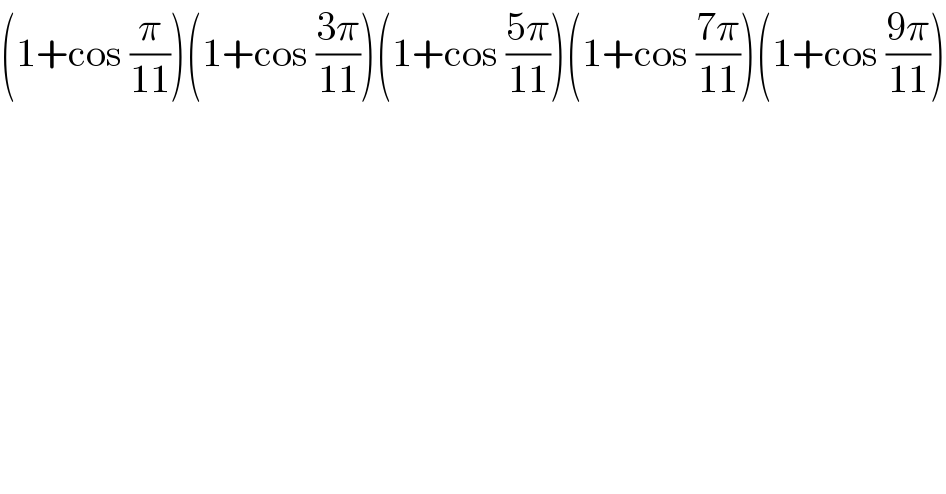
$$\left(\mathrm{1}+\mathrm{cos}\:\frac{\pi}{\mathrm{11}}\right)\left(\mathrm{1}+\mathrm{cos}\:\frac{\mathrm{3}\pi}{\mathrm{11}}\right)\left(\mathrm{1}+\mathrm{cos}\:\frac{\mathrm{5}\pi}{\mathrm{11}}\right)\left(\mathrm{1}+\mathrm{cos}\:\frac{\mathrm{7}\pi}{\mathrm{11}}\right)\left(\mathrm{1}+\mathrm{cos}\:\frac{\mathrm{9}\pi}{\mathrm{11}}\right) \\ $$
Commented by jagoll last updated on 11/Apr/20
![T= (2cos^2 ((π/(22))))(2cos^2 (((3π)/(22))))(2cos^2 (((5π)/(22)))) (2cos^2 (((7π)/(22))))(2cos^2 (((9π)/(22)))) = 32 [ cos (π/(22))cos ((3π)/(22))cos ((5π)/(22))cos ((7π)/(22))cos ((9π)/(22))]^2 cos ((((2k−1)π)/(22))) = −cos (π−((((2k−1)π)/(22)))) T= −32cos (((22−(2k−1))/(22))π) tobe continue](https://www.tinkutara.com/question/Q88572.png)
$$\mathrm{T}=\:\left(\mathrm{2cos}\:^{\mathrm{2}} \left(\frac{\pi}{\mathrm{22}}\right)\right)\left(\mathrm{2cos}^{\mathrm{2}} \:\left(\frac{\mathrm{3}\pi}{\mathrm{22}}\right)\right)\left(\mathrm{2cos}\:^{\mathrm{2}} \left(\frac{\mathrm{5}\pi}{\mathrm{22}}\right)\right) \\ $$$$\left(\mathrm{2cos}\:^{\mathrm{2}} \left(\frac{\mathrm{7}\pi}{\mathrm{22}}\right)\right)\left(\mathrm{2cos}\:^{\mathrm{2}} \left(\frac{\mathrm{9}\pi}{\mathrm{22}}\right)\right) \\ $$$$=\:\mathrm{32}\:\left[\:\mathrm{cos}\:\frac{\pi}{\mathrm{22}}\mathrm{cos}\:\frac{\mathrm{3}\pi}{\mathrm{22}}\mathrm{cos}\:\frac{\mathrm{5}\pi}{\mathrm{22}}\mathrm{cos}\:\frac{\mathrm{7}\pi}{\mathrm{22}}\mathrm{cos}\:\frac{\mathrm{9}\pi}{\mathrm{22}}\right]^{\mathrm{2}} \\ $$$$\mathrm{cos}\:\left(\frac{\left(\mathrm{2k}−\mathrm{1}\right)\pi}{\mathrm{22}}\right)\:=\:−\mathrm{cos}\:\left(\pi−\left(\frac{\left(\mathrm{2k}−\mathrm{1}\right)\pi}{\mathrm{22}}\right)\right) \\ $$$$\mathrm{T}=\:−\mathrm{32cos}\:\left(\frac{\mathrm{22}−\left(\mathrm{2k}−\mathrm{1}\right)}{\mathrm{22}}\pi\right) \\ $$$$\mathrm{tobe}\:\mathrm{continue} \\ $$
