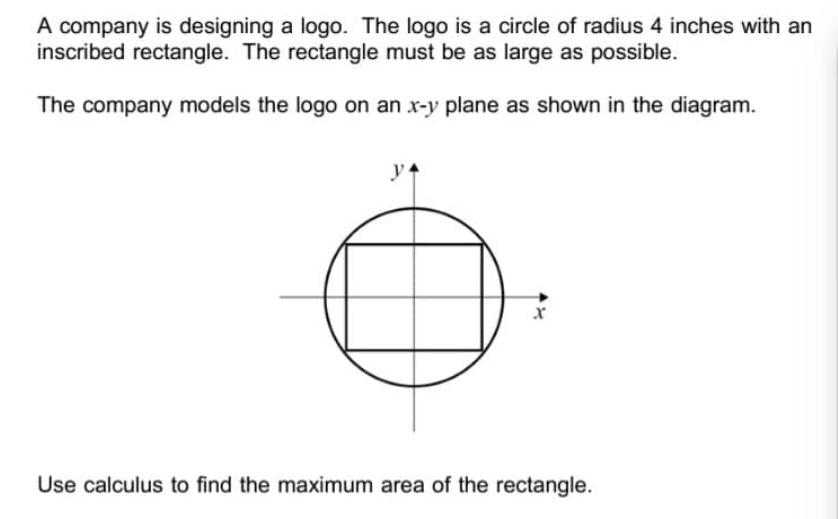
Question Number 155203 by nadovic last updated on 26/Sep/21
Answered by TheHoneyCat last updated on 29/Sep/21
![let O be the center of the circle let A be a vertice of the rectangle let θ be an angle (in radian) between one of the two axis (Oz or Oy) and the (OA) line The dimentions of the rectangle are (2cosθ,2sinθ) (or the opposite depending on your definition) Hence the area A of the rectangle is : A=4∣cosθ.sinθ∣ let a=cos×sin ∣a∣ is a π/2 periodical function also on [0,π/2] ∣a∣=a so let us sudy the restriction of a to this set: (da/dθ)=((d cos)/dθ)sin + ((d sin)/dθ)cos =−sin^2 +cos^2 so on this restriction a′(θ)=0 ⇔ (cosθ)^2 =(sinθ)^2 ⇔cosθ=sinθ (caus′ they are positiv on the interval) ⇔θ=^π /_4 ⇔cosθ=sinθ=(√2)/2 ⇔a(θ)=(1/2) Hence, the maximum area of the rectangle is that of a square ie: A=2](https://www.tinkutara.com/question/Q155368.png)
$$\mathrm{let}\:\mathrm{O}\:\mathrm{be}\:\mathrm{the}\:\mathrm{center}\:\mathrm{of}\:\mathrm{the}\:\mathrm{circle} \\ $$$$\mathrm{let}\:\mathrm{A}\:\mathrm{be}\:\mathrm{a}\:\mathrm{vertice}\:\mathrm{of}\:\mathrm{the}\:\mathrm{rectangle} \\ $$$$\mathrm{let}\:\theta\:\mathrm{be}\:\mathrm{an}\:\mathrm{angle}\:\left(\mathrm{in}\:\mathrm{radian}\right)\:\mathrm{between}\:\mathrm{one}\:\mathrm{of} \\ $$$$\mathrm{the}\:\mathrm{two}\:\mathrm{axis}\:\left(\mathrm{O}{z}\:\mathrm{or}\:\mathrm{O}{y}\right)\:\mathrm{and}\:\mathrm{the}\:\left(\mathrm{OA}\right)\:\mathrm{line} \\ $$$$ \\ $$$$\mathrm{The}\:\mathrm{dimentions}\:\mathrm{of}\:\mathrm{the}\:\mathrm{rectangle}\:\mathrm{are} \\ $$$$\left(\mathrm{2cos}\theta,\mathrm{2sin}\theta\right)\:\left({or}\:{the}\:{opposite}\:{depending}\right. \\ $$$$\left.{on}\:{your}\:{definition}\right) \\ $$$$ \\ $$$$\mathrm{Hence}\:\mathrm{the}\:\mathrm{area}\:\mathscr{A}\:\mathrm{of}\:\mathrm{the}\:\mathrm{rectangle}\:\mathrm{is}\:: \\ $$$$\mathscr{A}=\mathrm{4}\mid\mathrm{cos}\theta.\mathrm{sin}\theta\mid \\ $$$$\mathrm{let}\:{a}=\mathrm{cos}×\mathrm{sin} \\ $$$$\mid{a}\mid\:\mathrm{is}\:\mathrm{a}\:\pi/\mathrm{2}\:\mathrm{periodical}\:\mathrm{function} \\ $$$$\mathrm{also}\:\mathrm{on}\:\left[\mathrm{0},\pi/\mathrm{2}\right]\:\mid{a}\mid={a}\:\mathrm{so}\:\mathrm{let}\:\mathrm{us}\:\mathrm{sudy}\:\mathrm{the} \\ $$$$\mathrm{restriction}\:\mathrm{of}\:\mathrm{a}\:\mathrm{to}\:\mathrm{this}\:\mathrm{set}: \\ $$$$ \\ $$$$\frac{\mathrm{d}{a}}{\mathrm{d}\theta}=\frac{\mathrm{d}\:\mathrm{cos}}{\mathrm{d}\theta}\mathrm{sin}\:+\:\frac{\mathrm{d}\:\mathrm{sin}}{\mathrm{d}\theta}\mathrm{cos} \\ $$$$=−\mathrm{sin}^{\mathrm{2}} +\mathrm{cos}^{\mathrm{2}} \\ $$$$\mathrm{so}\:\mathrm{on}\:\mathrm{this}\:\mathrm{restriction} \\ $$$${a}'\left(\theta\right)=\mathrm{0}\:\Leftrightarrow\:\left(\mathrm{cos}\theta\right)^{\mathrm{2}} =\left(\mathrm{sin}\theta\right)^{\mathrm{2}} \\ $$$$\Leftrightarrow\mathrm{cos}\theta=\mathrm{sin}\theta\:\left({caus}'\:{they}\:{are}\:{positiv}\:{on}\:{the}\:\right. \\ $$$$\left.{interval}\right) \\ $$$$\Leftrightarrow\theta=^{\pi} /_{\mathrm{4}} \\ $$$$\Leftrightarrow\mathrm{cos}\theta=\mathrm{sin}\theta=\sqrt{\mathrm{2}}/\mathrm{2} \\ $$$$\Leftrightarrow{a}\left(\theta\right)=\frac{\mathrm{1}}{\mathrm{2}} \\ $$$$ \\ $$$$ \\ $$$$\mathrm{Hence},\:\mathrm{the}\:\mathrm{maximum}\:\mathrm{area}\:\mathrm{of}\:\mathrm{the}\:\mathrm{rectangle} \\ $$$$\mathrm{is}\:\mathrm{that}\:\mathrm{of}\:\mathrm{a}\:\mathrm{square}\:{ie}: \\ $$$$\mathscr{A}=\mathrm{2} \\ $$
Commented by nadovic last updated on 29/Sep/21
$${Sir},\:{the}\:{area}\:{is}\:{given}\:{as}\:\mathrm{32}\:{sq}.\:{in}. \\ $$
