Question Number 89978 by jagoll last updated on 20/Apr/20
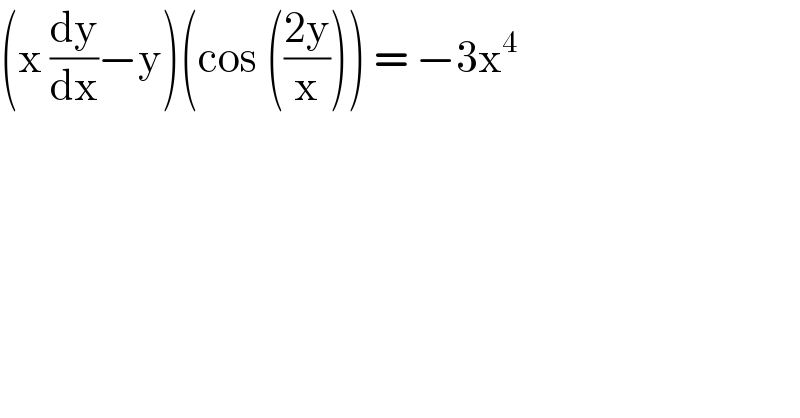
$$\left(\mathrm{x}\:\frac{\mathrm{dy}}{\mathrm{dx}}−\mathrm{y}\right)\left(\mathrm{cos}\:\left(\frac{\mathrm{2y}}{\mathrm{x}}\right)\right)\:=\:−\mathrm{3x}^{\mathrm{4}} \\ $$
Commented by john santu last updated on 20/Apr/20
![[ let y = ux ] ⇒(dy/dx) = u + x(du/dx) {ux +x^2 (du/dx) −ux }(cos 2u) = −3x^4 cos (2u) x^2 (du/dx) = −3x^4 cos (2u) du = −3x^2 dx ∫ cos (2u) du = ∫−3x^2 dx (1/2)sin (2u) = −x^3 +c sin (((2y)/x)) = −2x^3 +C ((2y)/x) = sin^(−1) (C−2x^3 ) y = ((xsin^(−1) (C−2x^3 ))/2)](https://www.tinkutara.com/question/Q89979.png)
$$\left[\:{let}\:{y}\:=\:{ux}\:\right]\:\Rightarrow\frac{{dy}}{{dx}}\:=\:{u}\:+\:{x}\frac{{du}}{{dx}} \\ $$$$\left\{{ux}\:+{x}^{\mathrm{2}} \:\frac{{du}}{{dx}}\:−{ux}\:\right\}\left(\mathrm{cos}\:\mathrm{2}{u}\right)\:=\:−\mathrm{3}{x}^{\mathrm{4}} \\ $$$$\mathrm{cos}\:\left(\mathrm{2}{u}\right)\:{x}^{\mathrm{2}} \:\frac{{du}}{{dx}}\:=\:−\mathrm{3}{x}^{\mathrm{4}} \\ $$$$\mathrm{cos}\:\left(\mathrm{2}{u}\right)\:{du}\:=\:−\mathrm{3}{x}^{\mathrm{2}} \:{dx} \\ $$$$\int\:\mathrm{cos}\:\left(\mathrm{2}{u}\right)\:{du}\:=\:\int−\mathrm{3}{x}^{\mathrm{2}} \:{dx} \\ $$$$\frac{\mathrm{1}}{\mathrm{2}}\mathrm{sin}\:\left(\mathrm{2}{u}\right)\:=\:−{x}^{\mathrm{3}} \:+{c}\: \\ $$$$\mathrm{sin}\:\left(\frac{\mathrm{2}{y}}{{x}}\right)\:=\:−\mathrm{2}{x}^{\mathrm{3}} +{C}\: \\ $$$$\frac{\mathrm{2}{y}}{{x}}\:=\:\mathrm{sin}^{−\mathrm{1}} \left({C}−\mathrm{2}{x}^{\mathrm{3}} \right)\: \\ $$$${y}\:=\:\frac{{x}\mathrm{sin}^{−\mathrm{1}} \left({C}−\mathrm{2}{x}^{\mathrm{3}} \right)}{\mathrm{2}} \\ $$
