Question Number 90291 by mathmax by abdo last updated on 22/Apr/20
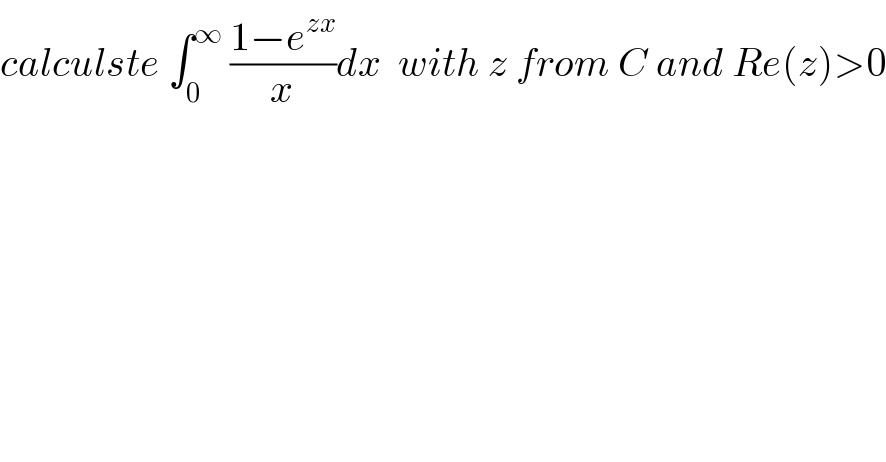
$${calculste}\:\int_{\mathrm{0}} ^{\infty} \:\frac{\mathrm{1}−{e}^{{zx}} }{{x}}{dx}\:\:{with}\:{z}\:{from}\:{C}\:{and}\:{Re}\left({z}\right)>\mathrm{0} \\ $$
Commented by mathmax by abdo last updated on 22/Apr/20

$${sorry}\:{Re}\left({z}\right)<\mathrm{0}\:. \\ $$
Commented by mathmax by abdo last updated on 23/Apr/20
![let f(z) =∫_0 ^∞ ((1−e^(zx) )/x)dx ⇒f^′ (z) =∫_0 ^∞ (∂/∂z)(((1−e^(zx) )/x))dx =−∫_0 ^∞ e^(zx) dx =−[(1/z)e^(zx) ]_0 ^(+∞) =−(1/z)(−1)=(1/z) (Rez<0) ⇒ f(z) =lnz +K so if z =α+iβ (α<0) ⇒z =(√(α^2 +β^2 ))e^(iarctan((β/α))) ⇒ ln(z) =(1/2)ln(α^2 +β^2 ) +iarctan((β/α)) ⇒ f(z)=(1/2)ln(α^2 +β^2 )+iarctan((β/α))+K rest to find K](https://www.tinkutara.com/question/Q90449.png)
$${let}\:{f}\left({z}\right)\:=\int_{\mathrm{0}} ^{\infty} \:\frac{\mathrm{1}−{e}^{{zx}} }{{x}}{dx}\:\Rightarrow{f}^{'} \left({z}\right)\:=\int_{\mathrm{0}} ^{\infty} \frac{\partial}{\partial{z}}\left(\frac{\mathrm{1}−{e}^{{zx}} }{{x}}\right){dx} \\ $$$$=−\int_{\mathrm{0}} ^{\infty} \:{e}^{{zx}} \:{dx}\:=−\left[\frac{\mathrm{1}}{{z}}{e}^{{zx}} \right]_{\mathrm{0}} ^{+\infty} \:\:=−\frac{\mathrm{1}}{{z}}\left(−\mathrm{1}\right)=\frac{\mathrm{1}}{{z}}\:\:\left({Rez}<\mathrm{0}\right)\:\Rightarrow \\ $$$${f}\left({z}\right)\:={lnz}\:+{K}\:\:{so}\:{if}\:{z}\:=\alpha+{i}\beta\:\:\:\:\:\left(\alpha<\mathrm{0}\right)\:\Rightarrow{z}\:=\sqrt{\alpha^{\mathrm{2}} \:+\beta^{\mathrm{2}} }{e}^{{iarctan}\left(\frac{\beta}{\alpha}\right)} \:\Rightarrow \\ $$$${ln}\left({z}\right)\:=\frac{\mathrm{1}}{\mathrm{2}}{ln}\left(\alpha^{\mathrm{2}} \:+\beta^{\mathrm{2}} \right)\:+{iarctan}\left(\frac{\beta}{\alpha}\right)\:\Rightarrow \\ $$$${f}\left({z}\right)=\frac{\mathrm{1}}{\mathrm{2}}{ln}\left(\alpha^{\mathrm{2}} \:+\beta^{\mathrm{2}} \right)+{iarctan}\left(\frac{\beta}{\alpha}\right)+{K}\:\:{rest}\:{to}\:{find}\:\:{K} \\ $$$$ \\ $$
