Question Number 27595 by abdo imad last updated on 10/Jan/18
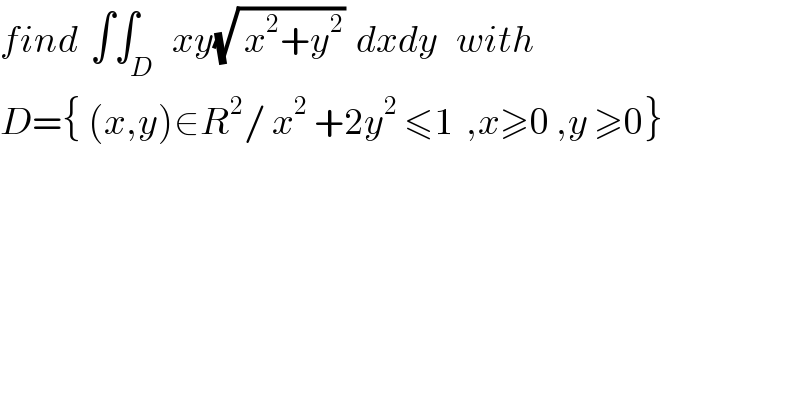
$${find}\:\:\int\int_{{D}} \:\:{xy}\sqrt{\:{x}^{\mathrm{2}} +{y}^{\mathrm{2}} }\:\:{dxdy}\:\:\:{with} \\ $$$${D}=\left\{\:\left({x},{y}\right)\in{R}^{\mathrm{2}} /\:{x}^{\mathrm{2}} \:+\mathrm{2}{y}^{\mathrm{2}} \:\leqslant\mathrm{1}\:\:,{x}\geqslant\mathrm{0}\:,{y}\:\geqslant\mathrm{0}\right\} \\ $$
Commented by abdo imad last updated on 15/Jan/18
![we use the polar coordinate let use the ch.x=rcosθ and y= (1/( (√2))) sinθ due to the diffeomorphisme we must have 0≤θ≤ (π/2) and 0≤r≤1 I=∫∫_D xy(√(x^2 +2y^2 )) dxdy= ∫∫_w Φof/j_Φ /dr dθ (r,θ)−(f_1 (r,θ) ,f_2 (r,θ))=(x y ) =(rcosθ ,(r/( (√2))) sinθ) M_j = (_((1/( (√2)))sinθ) ^(cosθ) _((r/( (√2)))cosθ)^(−rsinθ) ) I=∫∫_(0≤r≤1 and 0≤θ≤(π/2)) rcosθ.(r/( (√2))) sinθ r .(r/( (√2))) drdθ I= (1/2)∫_0^ ^1 r^4 ∫_0 ^(π/(2 )) cosθ sinθ dθ = (1/4) [(1/5) r^5 ]_0 ^1 ∫_0 ^(π/2) sin(2θ)dθ = (1/(40)) [−cos(2θ)]_0 ^(π/2) = (1/(20)) .](https://www.tinkutara.com/question/Q27877.png)
$${we}\:{use}\:{the}\:{polar}\:{coordinate}\:{let}\:{use}\:{the}\:{ch}.{x}={rcos}\theta \\ $$$${and}\:{y}=\:\frac{\mathrm{1}}{\:\sqrt{\mathrm{2}}}\:{sin}\theta\:\:\:{due}\:{to}\:{the}\:{diffeomorphisme}\:{we}\:{must}\:{have} \\ $$$$\:\mathrm{0}\leqslant\theta\leqslant\:\frac{\pi}{\mathrm{2}}\:{and}\:\:\mathrm{0}\leqslant{r}\leqslant\mathrm{1} \\ $$$${I}=\int\int_{{D}} {xy}\sqrt{{x}^{\mathrm{2}} +\mathrm{2}{y}^{\mathrm{2}} }\:{dxdy}=\:\int\int_{{w}} \:\Phi{of}/{j}_{\Phi} \:/{dr}\:{d}\theta \\ $$$$\left({r},\theta\right)−\left({f}_{\mathrm{1}} \left({r},\theta\right)\:,{f}_{\mathrm{2}} \left({r},\theta\right)\right)=\left({x}\:{y}\:\right)\:=\left({rcos}\theta\:,\frac{{r}}{\:\sqrt{\mathrm{2}}}\:{sin}\theta\right) \\ $$$${M}_{{j}} =\:\:\:\left(_{\frac{\mathrm{1}}{\:\sqrt{\mathrm{2}}}{sin}\theta} ^{{cos}\theta} \:\:\:\:_{\frac{{r}}{\:\sqrt{\mathrm{2}}}{cos}\theta} ^{−{rsin}\theta} \:\right) \\ $$$${I}=\int\int_{\mathrm{0}\leqslant{r}\leqslant\mathrm{1}\:{and}\:\mathrm{0}\leqslant\theta\leqslant\frac{\pi}{\mathrm{2}}} \:\:\:{rcos}\theta.\frac{{r}}{\:\sqrt{\mathrm{2}}}\:{sin}\theta\:{r}\:.\frac{{r}}{\:\sqrt{\mathrm{2}}}\:{drd}\theta \\ $$$${I}=\:\frac{\mathrm{1}}{\mathrm{2}}\int_{\mathrm{0}^{} } ^{\mathrm{1}} \:{r}^{\mathrm{4}} \:\:\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}\:}} \:{cos}\theta\:{sin}\theta\:{d}\theta\:=\:\frac{\mathrm{1}}{\mathrm{4}}\:\left[\frac{\mathrm{1}}{\mathrm{5}}\:{r}^{\mathrm{5}} \right]_{\mathrm{0}} ^{\mathrm{1}} \:\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \:{sin}\left(\mathrm{2}\theta\right){d}\theta \\ $$$$=\:\frac{\mathrm{1}}{\mathrm{40}}\:\left[−{cos}\left(\mathrm{2}\theta\right)\right]_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} =\:\:\frac{\mathrm{1}}{\mathrm{20}}\:. \\ $$
