Question Number 27693 by abdo imad last updated on 12/Jan/18
![1) calculate ∫∫_(]0,1]×]0,(π/2)]) ((dxdy)/(1+(xtany)^2 )) 2) find the value of ∫_0 ^(π/2) (t/(tant))dt .](https://www.tinkutara.com/question/Q27693.png)
$$\left.\mathrm{1}\right)\:{calculate}\:\:\int\int_{\left.\right]\left.\mathrm{0}\left.,\left.\mathrm{1}\right]×\right]\mathrm{0},\frac{\pi}{\mathrm{2}}\right]} \:\:\:\frac{{dxdy}}{\mathrm{1}+\left({xtany}\right)^{\mathrm{2}} } \\ $$$$\left.\mathrm{2}\right)\:{find}\:{the}\:{value}\:{of}\:\:\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \:\:\frac{{t}}{{tant}}{dt}\:. \\ $$
Commented by abdo imad last updated on 13/Jan/18
![1)let put I= ∫∫_(]0,1]×]0,(π/2)]) ((dxdy)/(1+(xtany)^2 )) I= ∫_0 ^1 (∫_0 ^(π/2) (dy/(1+x^2 tan^2 y)))dx but the ch. tany=t give ∫_0 ^(π/2) (dy/(1+x^2 tan^2 y)) = ∫_0 ^∞ (1/((1+x^2 t^2 ))) (dt/((1+t^2 ))) = (1/2) ∫_R (dt/((1+t^2 )(1+x^2 t^2 ))) let introduce the complex function f(z)= (1/((1+z^2 )(1+x^2 z^2 ))) f(z)= (1/(x^2 (z−i)(z+i)(z−(i/x))(z+(i/x))))( dont forget that 0<x≤1) the poles of f are i and −i and (i/x) and −(i/x) so ∫_R f(z)dz=2iπ( Re(f,i) +Re(f,(i/x))) but Res(f,i)=lim_(z−>i) (z−i)f(z)= (1/(x^2 (2i)(−1+(1/x^2 )))) = (1/(2i(1−x^2 ))) Re(f, (i/x))=lim_(z−>(i/x)) (z−(i/x))f(z)= (1/(x^2 (−(1/x^2 )+1)(((2i)/x)))) = (x/(2i(x^2 −1))) ∫_R f(z)dz= 2iπ( (1/(2i(1−x^2 ))) − (x/(2i(1−x^2 )))) = π((1−x)/(1−x^2 )) = (π/(1+x)) and ∫_0 ^(π/2) (dy/(1+x^2 tan^2 y)) = (π/(2(1+x))) ⇒ I= ∫_0 ^1 (π/(2(1+x))) dx =(π/2) [ln/1+x/]_0 ^1 = (π/2) ln2 2)by fubini therem we have also I=∫_0 ^(π/2) ( ∫_0 ^1 (dx/(1+(xtany)^2 )))dy and the ch. xtany=t give ∫_0 ^1 (dx/(1+(xtany)^2 ))= ∫_0 ^(tany) (1/(1+t^2 )) (dt/(tany)) =(1/(tany)) arctan(tany)= (y/(tany)) so I= ∫_0 ^(π/2) (y/(tany))dy ⇒∫_0 ^(π/2) (t/(tant)) dt = (π/2) ln(2).](https://www.tinkutara.com/question/Q27735.png)
$$\left.\mathrm{1}\right){let}\:{put}\:{I}=\:\int\int_{\left.\right]\left.\mathrm{0}\left.,\left.\mathrm{1}\right]×\right]\mathrm{0},\frac{\pi}{\mathrm{2}}\right]} \:\:\frac{{dxdy}}{\mathrm{1}+\left({xtany}\right)^{\mathrm{2}} } \\ $$$${I}=\:\int_{\mathrm{0}} ^{\mathrm{1}} \:\:\left(\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \:\frac{{dy}}{\mathrm{1}+{x}^{\mathrm{2}} {tan}^{\mathrm{2}} {y}}\right){dx}\:\:\:{but}\:{the}\:{ch}.\:{tany}={t}\:{give} \\ $$$$\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \:\:\frac{{dy}}{\mathrm{1}+{x}^{\mathrm{2}} {tan}^{\mathrm{2}} {y}}\:=\:\int_{\mathrm{0}} ^{\infty} \:\frac{\mathrm{1}}{\left(\mathrm{1}+{x}^{\mathrm{2}} {t}^{\mathrm{2}} \right)}\:\frac{{dt}}{\left(\mathrm{1}+{t}^{\mathrm{2}} \right)} \\ $$$$=\:\frac{\mathrm{1}}{\mathrm{2}}\:\int_{{R}} \:\:\:\:\frac{{dt}}{\left(\mathrm{1}+{t}^{\mathrm{2}} \right)\left(\mathrm{1}+{x}^{\mathrm{2}} {t}^{\mathrm{2}} \right)}\:{let}\:{introduce}\:{the}\:{complex}\:{function} \\ $$$${f}\left({z}\right)=\:\:\:\frac{\mathrm{1}}{\left(\mathrm{1}+{z}^{\mathrm{2}} \right)\left(\mathrm{1}+{x}^{\mathrm{2}} {z}^{\mathrm{2}} \right)} \\ $$$${f}\left({z}\right)=\:\:\:\frac{\mathrm{1}}{{x}^{\mathrm{2}} \left({z}−{i}\right)\left({z}+{i}\right)\left({z}−\frac{{i}}{{x}}\right)\left({z}+\frac{{i}}{{x}}\right)}\left(\:\:{dont}\:{forget}\:{that}\:\mathrm{0}<{x}\leqslant\mathrm{1}\right) \\ $$$${the}\:{poles}\:{of}\:{f}\:{are}\:{i}\:{and}\:−{i}\:{and}\:\frac{{i}}{{x}}\:{and}\:−\frac{{i}}{{x}}\:\:{so} \\ $$$$\int_{{R}} \:\:\:{f}\left({z}\right){dz}=\mathrm{2}{i}\pi\left(\:\:{Re}\left({f},{i}\right)\:+{Re}\left({f},\frac{{i}}{{x}}\right)\right)\:{but} \\ $$$${Res}\left({f},{i}\right)={lim}_{{z}−>{i}} \left({z}−{i}\right){f}\left({z}\right)=\:\:\frac{\mathrm{1}}{{x}^{\mathrm{2}} \left(\mathrm{2}{i}\right)\left(−\mathrm{1}+\frac{\mathrm{1}}{{x}^{\mathrm{2}} }\right)} \\ $$$$=\:\frac{\mathrm{1}}{\mathrm{2}{i}\left(\mathrm{1}−{x}^{\mathrm{2}} \right)} \\ $$$${Re}\left({f},\:\frac{{i}}{{x}}\right)={lim}_{{z}−>\frac{{i}}{{x}}} \:\left({z}−\frac{{i}}{{x}}\right){f}\left({z}\right)=\:\:\:\:\:\:\:\frac{\mathrm{1}}{{x}^{\mathrm{2}} \left(−\frac{\mathrm{1}}{{x}^{\mathrm{2}} }+\mathrm{1}\right)\left(\frac{\mathrm{2}{i}}{{x}}\right)} \\ $$$$=\:\:\frac{{x}}{\mathrm{2}{i}\left({x}^{\mathrm{2}} −\mathrm{1}\right)} \\ $$$$\int_{{R}} {f}\left({z}\right){dz}=\:\mathrm{2}{i}\pi\left(\:\:\:\frac{\mathrm{1}}{\mathrm{2}{i}\left(\mathrm{1}−{x}^{\mathrm{2}} \right)}\:−\:\frac{{x}}{\mathrm{2}{i}\left(\mathrm{1}−{x}^{\mathrm{2}} \right)}\right) \\ $$$$=\:\pi\frac{\mathrm{1}−{x}}{\mathrm{1}−{x}^{\mathrm{2}} }\:=\:\frac{\pi}{\mathrm{1}+{x}}\:\:{and}\:\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \:\:\:\frac{{dy}}{\mathrm{1}+{x}^{\mathrm{2}} {tan}^{\mathrm{2}} {y}}\:=\:\frac{\pi}{\mathrm{2}\left(\mathrm{1}+{x}\right)} \\ $$$$\Rightarrow\:{I}=\:\int_{\mathrm{0}} ^{\mathrm{1}} \:\frac{\pi}{\mathrm{2}\left(\mathrm{1}+{x}\right)}\:{dx}\:=\frac{\pi}{\mathrm{2}}\:\left[{ln}/\mathrm{1}+{x}/\right]_{\mathrm{0}} ^{\mathrm{1}} =\:\frac{\pi}{\mathrm{2}}\:{ln}\mathrm{2} \\ $$$$\left.\mathrm{2}\right){by}\:{fubini}\:{therem}\:{we}\:{have}\:{also}\: \\ $$$${I}=\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \left(\:\int_{\mathrm{0}} ^{\mathrm{1}} \:\:\frac{{dx}}{\mathrm{1}+\left({xtany}\right)^{\mathrm{2}} }\right){dy}\:{and}\:{the}\:{ch}.\:{xtany}={t}\:{give} \\ $$$$\int_{\mathrm{0}} ^{\mathrm{1}} \:\:\:\:\frac{{dx}}{\mathrm{1}+\left({xtany}\right)^{\mathrm{2}} }=\:\int_{\mathrm{0}} ^{{tany}} \:\:\:\frac{\mathrm{1}}{\mathrm{1}+{t}^{\mathrm{2}} }\:\frac{{dt}}{{tany}} \\ $$$$=\frac{\mathrm{1}}{{tany}}\:{arctan}\left({tany}\right)=\:\frac{{y}}{{tany}}\:{so} \\ $$$${I}=\:\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \:\frac{{y}}{{tany}}{dy}\:\:\Rightarrow\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \:\:\:\frac{{t}}{{tant}}\:{dt}\:=\:\frac{\pi}{\mathrm{2}}\:{ln}\left(\mathrm{2}\right). \\ $$
Answered by sma3l2996 last updated on 13/Jan/18
![1: I=∫∫_(]0,1]×]0,π/2]) ((dxdy)/((xtany)^2 ))=lim_(b→0) ∫_b ^(π/2) (lim_(a→0) ∫_a ^1 (dx/(1+(xtany)^2 )))dy let t=xtany⇒dt=tanydx I=lim_(b→0) ∫_b ^(π/2) (1/(tany))×lim_(a→0) (∫_a ^(tany) (dt/(1+t^2 )))dy =lim_(b→0) ∫_b ^(π/2) (1/(tany))×lim_(a→0) [tan^(−1) (t)]_a ^(tany) dy =lim_(b→0) ∫_b ^(π/2) (1/(tany))(y−0)dy=lim_(b→0) ∫_0 ^(π/2) ((ydy)/(tany)) let z=e^(iy) I=−∫_Δ ((ln(z)(z^2 −1))/(z^2 +1))×(dz/z) let f(z)=((ln(z)(z^2 −1))/(z(z+i)(z−i))) so I=−2iπRes(f,i)=−2iπ(((ln(i)(−2))/(−2))) I=π^2](https://www.tinkutara.com/question/Q27703.png)
$$\mathrm{1}:\:\:{I}=\int\int_{\left.\right]\left.\mathrm{0}\left.,\left.\mathrm{1}\right]×\right]\mathrm{0},\pi/\mathrm{2}\right]} \frac{{dxdy}}{\left({xtany}\right)^{\mathrm{2}} }=\underset{{b}\rightarrow\mathrm{0}} {{lim}}\int_{{b}} ^{\pi/\mathrm{2}} \left(\underset{{a}\rightarrow\mathrm{0}} {{lim}}\int_{{a}} ^{\mathrm{1}} \frac{{dx}}{\mathrm{1}+\left({xtany}\right)^{\mathrm{2}} }\right){dy} \\ $$$${let}\:\:{t}={xtany}\Rightarrow{dt}={tanydx} \\ $$$${I}=\underset{{b}\rightarrow\mathrm{0}} {{lim}}\int_{{b}} ^{\pi/\mathrm{2}} \frac{\mathrm{1}}{{tany}}×\underset{{a}\rightarrow\mathrm{0}} {{lim}}\left(\int_{{a}} ^{{tany}} \frac{{dt}}{\mathrm{1}+{t}^{\mathrm{2}} }\right){dy} \\ $$$$=\underset{{b}\rightarrow\mathrm{0}} {{lim}}\int_{{b}} ^{\pi/\mathrm{2}} \frac{\mathrm{1}}{{tany}}×\underset{{a}\rightarrow\mathrm{0}} {{lim}}\left[{tan}^{−\mathrm{1}} \left({t}\right)\right]_{{a}} ^{{tany}} {dy} \\ $$$$=\underset{{b}\rightarrow\mathrm{0}} {{lim}}\int_{{b}} ^{\pi/\mathrm{2}} \frac{\mathrm{1}}{{tany}}\left({y}−\mathrm{0}\right){dy}=\underset{{b}\rightarrow\mathrm{0}} {{lim}}\int_{\mathrm{0}} ^{\pi/\mathrm{2}} \frac{{ydy}}{{tany}} \\ $$$${let}\:{z}={e}^{{iy}} \\ $$$${I}=−\int_{\Delta} \frac{{ln}\left({z}\right)\left({z}^{\mathrm{2}} −\mathrm{1}\right)}{{z}^{\mathrm{2}} +\mathrm{1}}×\frac{{dz}}{{z}} \\ $$$${let}\:{f}\left({z}\right)=\frac{{ln}\left({z}\right)\left({z}^{\mathrm{2}} −\mathrm{1}\right)}{{z}\left({z}+{i}\right)\left({z}−{i}\right)} \\ $$$${so}\:\:{I}=−\mathrm{2}{i}\pi{Res}\left({f},{i}\right)=−\mathrm{2}{i}\pi\left(\frac{{ln}\left({i}\right)\left(−\mathrm{2}\right)}{−\mathrm{2}}\right) \\ $$$${I}=\pi^{\mathrm{2}} \\ $$
Commented by abdo imad last updated on 13/Jan/18
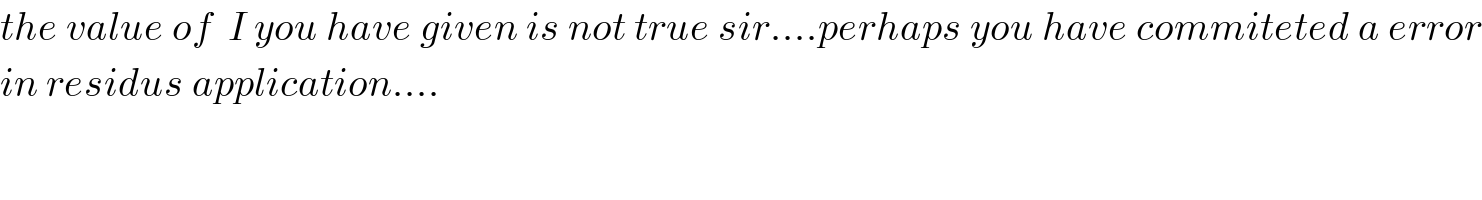
$${the}\:{value}\:{of}\:\:{I}\:{you}\:{have}\:{given}\:{is}\:{not}\:{true}\:{sir}….{perhaps}\:{you}\:{have}\:{commiteted}\:{a}\:{error} \\ $$$${in}\:{residus}\:{application}…. \\ $$$$ \\ $$
