Question Number 160391 by akolade last updated on 29/Nov/21
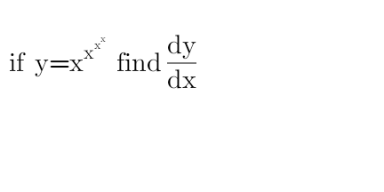
Answered by FongXD last updated on 29/Nov/21
![• (x^x )′=(e^(xlnx) )′=e^(xlnx) (lnx+1)=x^x (lnx+1) • (x^x^x )′=(e^(x^x lnx) )′=e^(x^x lnx) (x^x lnx)′ =x^x^x [(x^x )′lnx+(lnx)′x^x ] =x^x^x [x^x (lnx+1)lnx+x^(x−1) ] =x^(x^x +x−1) (xln^2 x+xlnx+1) ⇒ (dy/dx)=y′=(x^x^x^x )′=(e^(x^x^x lnx) )′=e^(x^x^x lnx) (x^x^x lnx)′ =x^x^x^x [(x^x^x )′lnx+(lnx)′x^x^x ] =x^x^x^x [x^(x^x +x−1) (xln^2 x+xlnx+1)lnx+x^(x^x −1) ] =x^(x^x^x +x^x −1) [x^x (xln^3 x+xln^2 x+lnx)+1] =x^(x^x^x +x^x −1) (x^(x+1) ln^3 x+x^(x+1) ln^2 x+lnx+1)](https://www.tinkutara.com/question/Q160396.png)
$$\bullet\:\left(\mathrm{x}^{\mathrm{x}} \right)'=\left(\mathrm{e}^{\mathrm{xlnx}} \right)'=\mathrm{e}^{\mathrm{xlnx}} \left(\mathrm{lnx}+\mathrm{1}\right)=\mathrm{x}^{\mathrm{x}} \left(\mathrm{lnx}+\mathrm{1}\right) \\ $$$$\bullet\:\left(\mathrm{x}^{\mathrm{x}^{\mathrm{x}} } \right)'=\left(\mathrm{e}^{\mathrm{x}^{\mathrm{x}} \mathrm{lnx}} \right)'=\mathrm{e}^{\mathrm{x}^{\mathrm{x}} \mathrm{lnx}} \left(\mathrm{x}^{\mathrm{x}} \mathrm{lnx}\right)' \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:=\mathrm{x}^{\mathrm{x}^{\mathrm{x}} } \left[\left(\mathrm{x}^{\mathrm{x}} \right)'\mathrm{lnx}+\left(\mathrm{lnx}\right)'\mathrm{x}^{\mathrm{x}} \right] \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:=\mathrm{x}^{\mathrm{x}^{\mathrm{x}} } \left[\mathrm{x}^{\mathrm{x}} \left(\mathrm{lnx}+\mathrm{1}\right)\mathrm{lnx}+\mathrm{x}^{\mathrm{x}−\mathrm{1}} \right] \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:=\mathrm{x}^{\mathrm{x}^{\mathrm{x}} +\mathrm{x}−\mathrm{1}} \left(\mathrm{xln}^{\mathrm{2}} \mathrm{x}+\mathrm{xlnx}+\mathrm{1}\right) \\ $$$$\Rightarrow\:\frac{\mathrm{dy}}{\mathrm{dx}}=\mathrm{y}'=\left(\mathrm{x}^{\mathrm{x}^{\mathrm{x}^{\mathrm{x}} } } \right)'=\left(\mathrm{e}^{\mathrm{x}^{\mathrm{x}^{\mathrm{x}} } \mathrm{lnx}} \right)'=\mathrm{e}^{\mathrm{x}^{\mathrm{x}^{\mathrm{x}} } \mathrm{lnx}} \left(\mathrm{x}^{\mathrm{x}^{\mathrm{x}} } \mathrm{lnx}\right)' \\ $$$$\:\:\:\:\:\:\:\:\:\:\:=\mathrm{x}^{\mathrm{x}^{\mathrm{x}^{\mathrm{x}} } } \left[\left(\mathrm{x}^{\mathrm{x}^{\mathrm{x}} } \right)'\mathrm{lnx}+\left(\mathrm{lnx}\right)'\mathrm{x}^{\mathrm{x}^{\mathrm{x}} } \right] \\ $$$$\:\:\:\:\:\:\:\:\:\:\:=\mathrm{x}^{\mathrm{x}^{\mathrm{x}^{\mathrm{x}} } } \left[\mathrm{x}^{\mathrm{x}^{\mathrm{x}} +\mathrm{x}−\mathrm{1}} \left(\mathrm{xln}^{\mathrm{2}} \mathrm{x}+\mathrm{xlnx}+\mathrm{1}\right)\mathrm{lnx}+\mathrm{x}^{\mathrm{x}^{\mathrm{x}} −\mathrm{1}} \right] \\ $$$$\:\:\:\:\:\:\:\:\:\:\:=\mathrm{x}^{\mathrm{x}^{\mathrm{x}^{\mathrm{x}} } +\mathrm{x}^{\mathrm{x}} −\mathrm{1}} \left[\mathrm{x}^{\mathrm{x}} \left(\mathrm{xln}^{\mathrm{3}} \mathrm{x}+\mathrm{xln}^{\mathrm{2}} \mathrm{x}+\mathrm{lnx}\right)+\mathrm{1}\right] \\ $$$$\:\:\:\:\:\:\:\:\:\:\:=\mathrm{x}^{\mathrm{x}^{\mathrm{x}^{\mathrm{x}} } +\mathrm{x}^{\mathrm{x}} −\mathrm{1}} \left(\mathrm{x}^{\mathrm{x}+\mathrm{1}} \mathrm{ln}^{\mathrm{3}} \mathrm{x}+\mathrm{x}^{\mathrm{x}+\mathrm{1}} \mathrm{ln}^{\mathrm{2}} \mathrm{x}+\mathrm{lnx}+\mathrm{1}\right) \\ $$
