Question Number 161444 by cortano last updated on 18/Dec/21
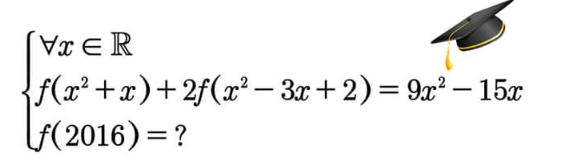
Commented by blackmamba last updated on 18/Dec/21
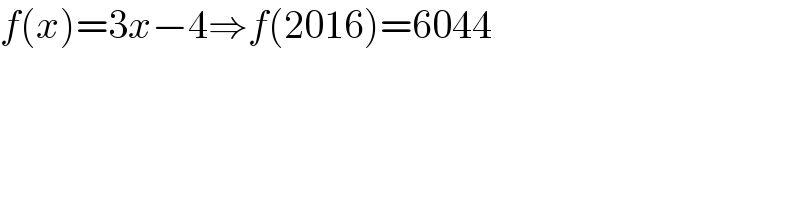
$${f}\left({x}\right)=\mathrm{3}{x}−\mathrm{4}\Rightarrow{f}\left(\mathrm{2016}\right)=\mathrm{6044} \\ $$
Commented by blackmamba last updated on 18/Dec/21
![f(x)=ax+b f(x^2 +x)=ax^2 +ax+b 2f(x^2 −3x+2)=2[(ax^2 −3ax+2a)+b] f(x)+2f(x^2 −3x+2)=3ax^2 −5ax+4a+3b { ((3a=9⇒a=3)),((4a+3b=0⇒3b=−12; b=−4)) :} ∴ f(x)= 3x−4⇒f(2016)=6044 3×2016−4 6044.0](https://www.tinkutara.com/question/Q161488.png)
$${f}\left({x}\right)={ax}+{b}\: \\ $$$${f}\left({x}^{\mathrm{2}} +{x}\right)={ax}^{\mathrm{2}} +{ax}+{b} \\ $$$$\mathrm{2}{f}\left({x}^{\mathrm{2}} −\mathrm{3}{x}+\mathrm{2}\right)=\mathrm{2}\left[\left({ax}^{\mathrm{2}} −\mathrm{3}{ax}+\mathrm{2}{a}\right)+{b}\right] \\ $$$${f}\left({x}\right)+\mathrm{2}{f}\left({x}^{\mathrm{2}} −\mathrm{3}{x}+\mathrm{2}\right)=\mathrm{3}{ax}^{\mathrm{2}} −\mathrm{5}{ax}+\mathrm{4}{a}+\mathrm{3}{b} \\ $$$$\:\begin{cases}{\mathrm{3}{a}=\mathrm{9}\Rightarrow{a}=\mathrm{3}}\\{\mathrm{4}{a}+\mathrm{3}{b}=\mathrm{0}\Rightarrow\mathrm{3}{b}=−\mathrm{12};\:{b}=−\mathrm{4}}\end{cases} \\ $$$$\therefore\:{f}\left({x}\right)=\:\mathrm{3}{x}−\mathrm{4}\Rightarrow{f}\left(\mathrm{2016}\right)=\mathrm{6044} \\ $$$$\mathrm{3}×\mathrm{2016}−\mathrm{4} \\ $$$$\mathrm{6044}.\mathrm{0} \\ $$
