Question Number 30427 by rahul 19 last updated on 22/Feb/18
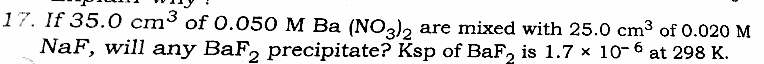
Commented by Tinkutara last updated on 22/Feb/18
Is the answer yes?
Commented by rahul 19 last updated on 22/Feb/18

$$\mathrm{actually},\:\mathrm{i}\:\mathrm{don}'\mathrm{t}\:\mathrm{know}\:\mathrm{correct}\:\mathrm{ans}. \\ $$$$\mathrm{it}\:\mathrm{came}\:\mathrm{in}\:\mathrm{my}\:\mathrm{final}\:\mathrm{exam}\:\mathrm{held}\:\mathrm{today}. \\ $$$$\mathrm{can}\:\mathrm{u}\:\mathrm{show}\:\mathrm{the}\:\mathrm{working}? \\ $$
Commented by Tinkutara last updated on 22/Feb/18

Commented by Tinkutara last updated on 23/Feb/18
![[Ba^(2+) ]=((1.75 m mol)/(60 mL))=(7/(240))M ∵ New volume=25+35=60 mL We do now [Ba^(2+) ][F^− ]^2 to calculate the solubility product of BaF_2 .](https://www.tinkutara.com/question/Q30536.png)
$$\left[{Ba}^{\mathrm{2}+} \right]=\frac{\mathrm{1}.\mathrm{75}\:{m}\:{mol}}{\mathrm{60}\:{mL}}=\frac{\mathrm{7}}{\mathrm{240}}{M} \\ $$$$\because\:{New}\:{volume}=\mathrm{25}+\mathrm{35}=\mathrm{60}\:{mL} \\ $$$${We}\:{do}\:{now}\:\left[{Ba}^{\mathrm{2}+} \right]\left[{F}^{−} \right]^{\mathrm{2}} \:{to}\:{calculate} \\ $$$${the}\:{solubility}\:{product}\:{of}\:{BaF}_{\mathrm{2}} . \\ $$
Commented by rahul 19 last updated on 22/Feb/18
![how [Ba^(2+) ]= 7/240? and also why [F^− ]^(2 ) , acc. to balanced eq. it should be [F^− ].](https://www.tinkutara.com/question/Q30465.png)
$$\mathrm{how}\:\left[\mathrm{Ba}^{\mathrm{2}+} \:\right]=\:\mathrm{7}/\mathrm{240}? \\ $$$$\mathrm{and}\:\mathrm{also}\:\mathrm{why}\:\left[\mathrm{F}^{−} \right]^{\mathrm{2}\:} \:,\:\mathrm{acc}.\:\mathrm{to}\:\mathrm{balanced}\:\mathrm{eq}. \\ $$$$\mathrm{it}\:\mathrm{should}\:\mathrm{be}\:\left[\mathrm{F}^{−} \right]. \\ $$
Commented by rahul 19 last updated on 23/Feb/18

$$\mathrm{ok},\mathrm{thanks}! \\ $$
