Question Number 96489 by Ar Brandon last updated on 01/Jun/20
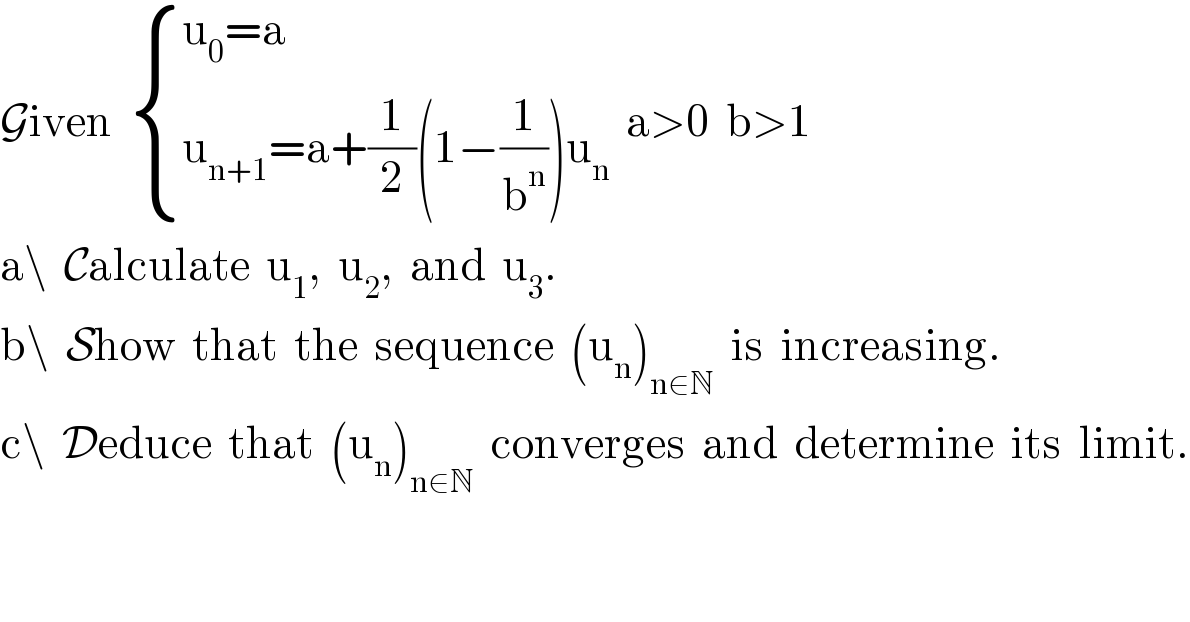
$$\mathcal{G}\mathrm{iven}\:\:\begin{cases}{\mathrm{u}_{\mathrm{0}} =\mathrm{a}}\\{\mathrm{u}_{\mathrm{n}+\mathrm{1}} =\mathrm{a}+\frac{\mathrm{1}}{\mathrm{2}}\left(\mathrm{1}−\frac{\mathrm{1}}{\mathrm{b}^{\mathrm{n}} }\right)\mathrm{u}_{\mathrm{n}} }\end{cases}\:\:\mathrm{a}>\mathrm{0}\:\:\mathrm{b}>\mathrm{1} \\ $$$$\mathrm{a}\backslash\:\:\mathcal{C}\mathrm{alculate}\:\:\mathrm{u}_{\mathrm{1}} ,\:\:\mathrm{u}_{\mathrm{2}} ,\:\:\mathrm{and}\:\:\mathrm{u}_{\mathrm{3}} . \\ $$$$\mathrm{b}\backslash\:\:\mathcal{S}\mathrm{how}\:\:\mathrm{that}\:\:\mathrm{the}\:\:\mathrm{sequence}\:\:\left(\mathrm{u}_{\mathrm{n}} \right)_{\mathrm{n}\in\mathbb{N}} \:\:\mathrm{is}\:\:\mathrm{increasing}. \\ $$$$\mathrm{c}\backslash\:\:\mathcal{D}\mathrm{educe}\:\:\mathrm{that}\:\:\left(\mathrm{u}_{\mathrm{n}} \right)_{\mathrm{n}\in\mathbb{N}} \:\:\mathrm{converges}\:\:\mathrm{and}\:\:\mathrm{determine}\:\:\mathrm{its}\:\:\mathrm{limit}. \\ $$
Answered by Rio Michael last updated on 01/Jun/20
![(a)u_0 = a ⇒ u_1 = a + (1/2)(1−(1/b^0 ))u_0 ⇒ u_1 = a u_2 = a + (1/2)(1 + (1/b))a = a[1 + (1/2)(1 − (1/b))] u_3 =[ a + (1/2)(1−(1/b^2 ))]{a[1 + (1/2)(1−(1/b))]} (b) n∈N and a > 0, b > 1 a [1 + (1/2)(1−(1/b))] > a for a > 0 and b > 1 [ a + (1/2)(1−(1/b^2 ))]{a[1 + (1/2)(1−(1/b))]} > a[1 + (1/2)(1−(1/b))] ⇒ the sequence is increasing for n ∈ N. (c) (1/2)(1−(1/b^n ))u_n < 1 ∀ n ∈ N ⇒ u_n is convergent](https://www.tinkutara.com/question/Q96492.png)
$$\left(\mathrm{a}\right){u}_{\mathrm{0}} \:=\:{a}\:\Rightarrow\:{u}_{\mathrm{1}} \:=\:{a}\:+\:\frac{\mathrm{1}}{\mathrm{2}}\left(\mathrm{1}−\frac{\mathrm{1}}{{b}^{\mathrm{0}} }\right){u}_{\mathrm{0}} \\ $$$$\Rightarrow\:{u}_{\mathrm{1}} \:=\:{a} \\ $$$${u}_{\mathrm{2}} \:=\:{a}\:+\:\frac{\mathrm{1}}{\mathrm{2}}\left(\mathrm{1}\:+\:\frac{\mathrm{1}}{{b}}\right){a}\:=\:{a}\left[\mathrm{1}\:+\:\frac{\mathrm{1}}{\mathrm{2}}\left(\mathrm{1}\:−\:\frac{\mathrm{1}}{{b}}\right)\right] \\ $$$${u}_{\mathrm{3}} \:=\left[\:{a}\:+\:\frac{\mathrm{1}}{\mathrm{2}}\left(\mathrm{1}−\frac{\mathrm{1}}{{b}^{\mathrm{2}} }\right)\right]\left\{{a}\left[\mathrm{1}\:+\:\frac{\mathrm{1}}{\mathrm{2}}\left(\mathrm{1}−\frac{\mathrm{1}}{{b}}\right)\right]\right\} \\ $$$$\left(\mathrm{b}\right)\:{n}\in\mathbb{N}\:\mathrm{and}\:{a}\:>\:\mathrm{0},\:{b}\:>\:\mathrm{1} \\ $$$${a}\:\left[\mathrm{1}\:+\:\frac{\mathrm{1}}{\mathrm{2}}\left(\mathrm{1}−\frac{\mathrm{1}}{{b}}\right)\right]\:>\:{a}\:\mathrm{for}\:\:{a}\:>\:\mathrm{0}\:\mathrm{and}\:{b}\:>\:\mathrm{1} \\ $$$$\left[\:{a}\:+\:\frac{\mathrm{1}}{\mathrm{2}}\left(\mathrm{1}−\frac{\mathrm{1}}{{b}^{\mathrm{2}} }\right)\right]\left\{{a}\left[\mathrm{1}\:+\:\frac{\mathrm{1}}{\mathrm{2}}\left(\mathrm{1}−\frac{\mathrm{1}}{{b}}\right)\right]\right\}\:>\:{a}\left[\mathrm{1}\:+\:\frac{\mathrm{1}}{\mathrm{2}}\left(\mathrm{1}−\frac{\mathrm{1}}{{b}}\right)\right]\: \\ $$$$\Rightarrow\:\mathrm{the}\:\mathrm{sequence}\:\mathrm{is}\:\mathrm{increasing}\:\mathrm{for}\:{n}\:\in\:\mathbb{N}. \\ $$$$\left(\mathrm{c}\right)\:\frac{\mathrm{1}}{\mathrm{2}}\left(\mathrm{1}−\frac{\mathrm{1}}{{b}^{{n}} }\right){u}_{{n}} \:<\:\mathrm{1}\:\forall\:{n}\:\in\:\mathbb{N}\:\Rightarrow\:{u}_{{n}} \:\mathrm{is}\:\mathrm{convergent} \\ $$$$ \\ $$
Commented by Ar Brandon last updated on 01/Jun/20
Wow, so fast !
Thank you ��
