Question-162071

Question Number 162071 by mr W last updated on 26/Dec/21

Commented by mr W last updated on 27/Dec/21

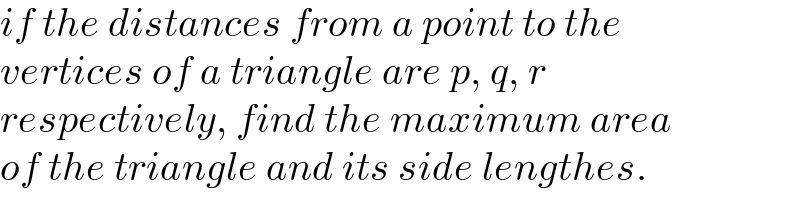
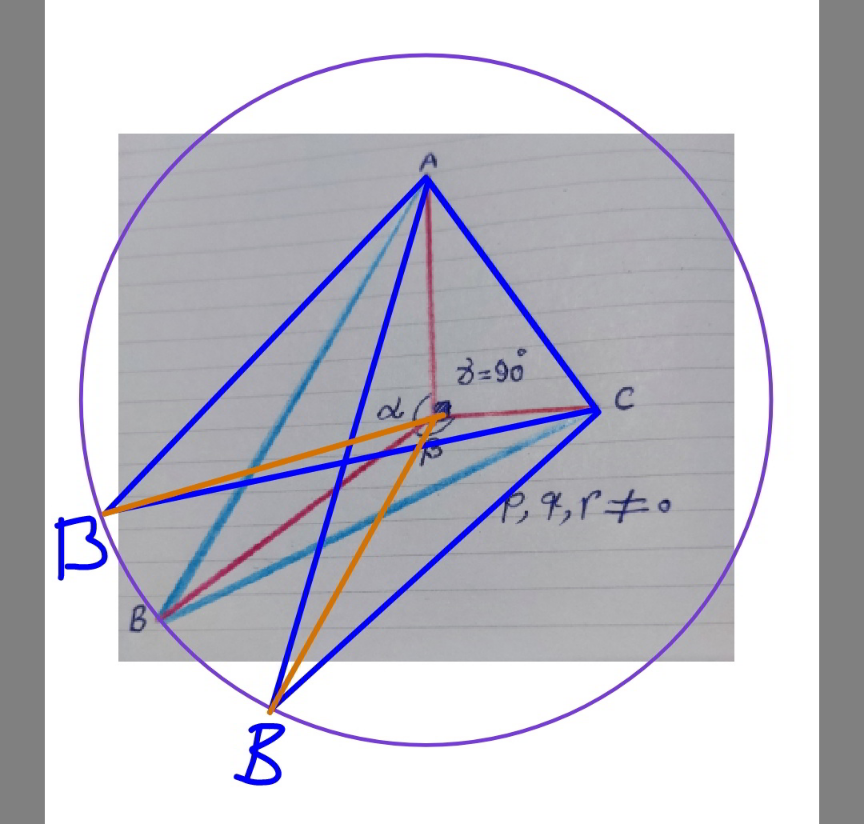
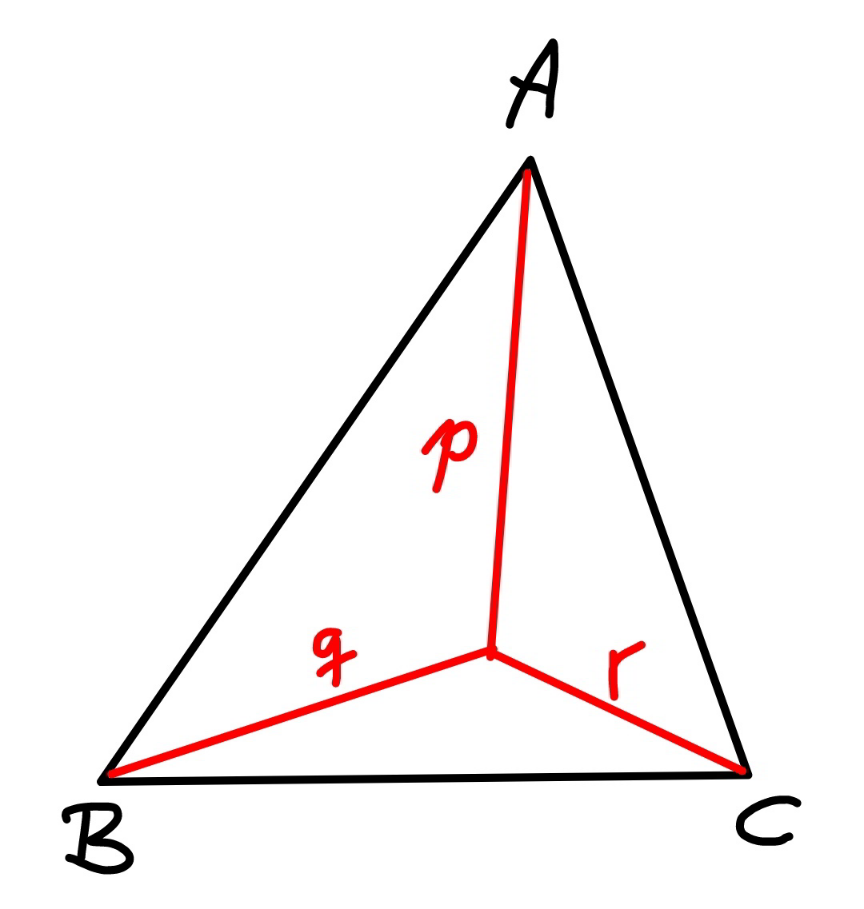
$${if}\:{the}\:{distances}\:{from}\:{a}\:{point}\:{to}\:{the} \\ $$$${vertices}\:{of}\:{a}\:{triangle}\:{are}\:{p},\:{q},\:{r} \\ $$$${respectively},\:{find}\:{the}\:{maximum}\:{area} \\ $$$${of}\:{the}\:{triangle}\:{and}\:{its}\:{side}\:{lengthes}. \\ $$

Commented by mr W last updated on 26/Dec/21

Commented by mr W last updated on 27/Dec/21

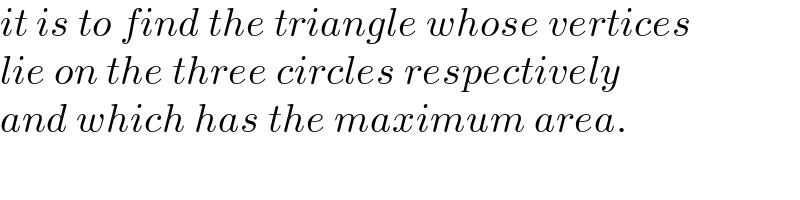
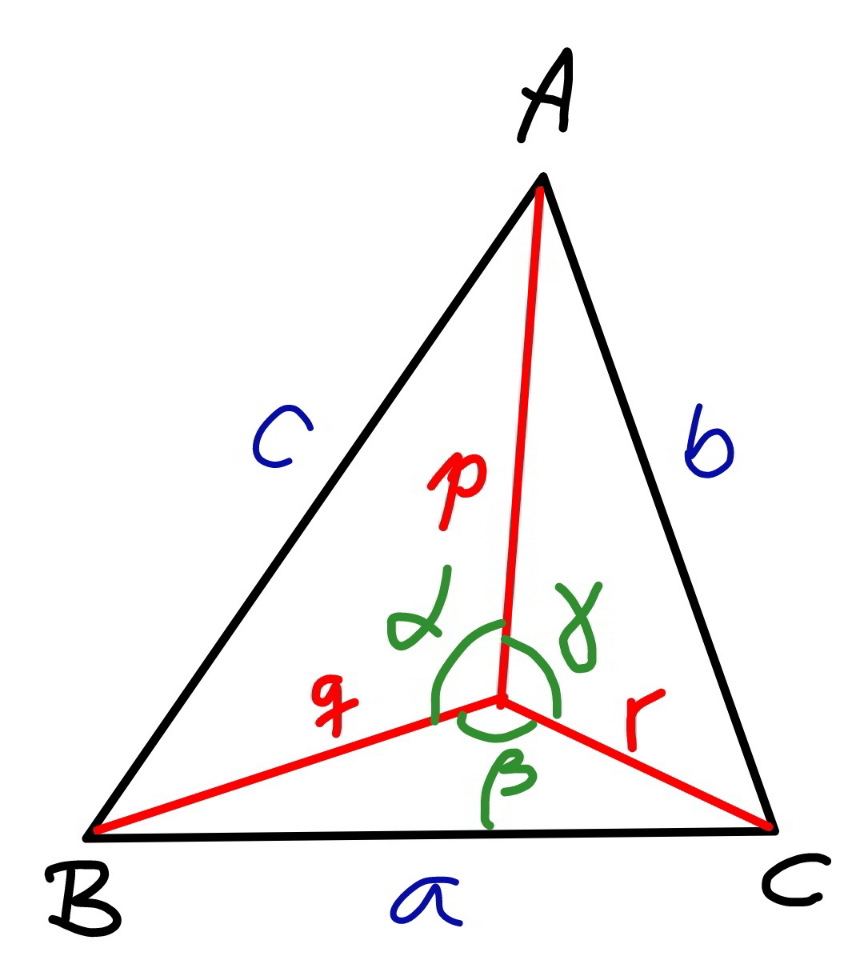
$${it}\:{is}\:{to}\:{find}\:{the}\:{triangle}\:{whose}\:{vertices} \\ $$$${lie}\:{on}\:{the}\:{three}\:{circles}\:{respectively} \\ $$$${and}\:{which}\:{has}\:{the}\:{maximum}\:{area}. \\ $$

Commented by Tawa11 last updated on 27/Dec/21

$$\mathrm{Wow},\:\mathrm{great}\:\mathrm{sir}. \\ $$

Commented by mr W last updated on 29/Dec/21

$${thanks}\:{for}\:{this}\:{vector}\:{way}\:{sir}! \\ $$$${i}\:{came}\:{to}\:{the}\:{same}\:{conclusion}\:{as} \\ $$$${stated}\:{below}. \\ $$

Commented by aleks041103 last updated on 29/Dec/21

Let p,q,r represent the vectors. S^→ =Se_z ^(→) =(1/2)(p^→ ×q^→ +q^→ ×r^→ +r^→ ×p^→ ) Since S is extremal, then we may variate the vectors as p^→ →p^→ +δp^→ q^→ →q^→ +δq^→ r^→ →r^→ +δr^→ And search for p^→ ,q^→ ,r^→ which make δS=0 and so δS^→ =0. Also the variations must be such that they preserve ∣p∣,∣q∣ and ∣r∣. δ(p^→ .p^→ )=2p^→ .δp^→ =0⇒p^→ ⊥δp^→ . Without restriction we may choose δq^→ =δr^→ =0 since the variations are arbitrary ⇒δSe_z ^(→) =(1/2)(δp^→ ×q^→ +r^→ ×δp^→ )=0 ⇒δp^→ ×(q^→ −r^→ )=0 ⇒p^→ ⊥δp^→ ∥q^→ −r^→ ⇒p^→ ⊥(q^→ −r^→ ) But (q^→ −r^→ ) is the side of the triangle opposite the vertex defined by p^→ . ⇒p^→ must be colinear to the height This must be true for q^→ and r^→ too. ⇒ The starting point is the orthocenter.

$${Let}\:{p},{q},{r}\:{represent}\:{the}\:{vectors}. \\ $$$$\overset{\rightarrow} {{S}}={S}\overset{\rightarrow} {{e}_{{z}} }=\frac{\mathrm{1}}{\mathrm{2}}\left(\overset{\rightarrow} {{p}}×\overset{\rightarrow} {{q}}+\overset{\rightarrow} {{q}}×\overset{\rightarrow} {{r}}+\overset{\rightarrow} {{r}}×\overset{\rightarrow} {{p}}\right) \\ $$$${Since}\:{S}\:{is}\:{extremal},\:{then}\:{we}\:{may} \\ $$$${variate}\:{the}\:{vectors}\:{as} \\ $$$$\overset{\rightarrow} {{p}}\rightarrow\overset{\rightarrow} {{p}}+\delta\overset{\rightarrow} {{p}} \\ $$$$\overset{\rightarrow} {{q}}\rightarrow\overset{\rightarrow} {{q}}+\delta\overset{\rightarrow} {{q}} \\ $$$$\overset{\rightarrow} {{r}}\rightarrow\overset{\rightarrow} {{r}}+\delta\overset{\rightarrow} {{r}} \\ $$$${And}\:{search}\:{for}\:\overset{\rightarrow} {{p}},\overset{\rightarrow} {{q}},\overset{\rightarrow} {{r}}\:{which}\:{make}\:\delta{S}=\mathrm{0}\:{and} \\ $$$${so}\:\delta\overset{\rightarrow} {{S}}=\mathrm{0}. \\ $$$${Also}\:{the}\:{variations}\:{must}\:{be}\:{such}\:{that} \\ $$$${they}\:{preserve}\:\mid{p}\mid,\mid{q}\mid\:{and}\:\mid{r}\mid. \\ $$$$\delta\left(\overset{\rightarrow} {{p}}.\overset{\rightarrow} {{p}}\right)=\mathrm{2}\overset{\rightarrow} {{p}}.\delta\overset{\rightarrow} {{p}}=\mathrm{0}\Rightarrow\overset{\rightarrow} {{p}}\bot\delta\overset{\rightarrow} {{p}}. \\ $$$${Without}\:{restriction}\:{we}\:{may}\:{choose} \\ $$$$\delta\overset{\rightarrow} {{q}}=\delta\overset{\rightarrow} {{r}}=\mathrm{0}\:{since}\:{the}\:{variations}\:{are}\:{arbitrary} \\ $$$$\Rightarrow\delta{S}\overset{\rightarrow} {{e}_{{z}} }=\frac{\mathrm{1}}{\mathrm{2}}\left(\delta\overset{\rightarrow} {{p}}×\overset{\rightarrow} {{q}}+\overset{\rightarrow} {{r}}×\delta\overset{\rightarrow} {{p}}\right)=\mathrm{0} \\ $$$$\Rightarrow\delta\overset{\rightarrow} {{p}}×\left(\overset{\rightarrow} {{q}}−\overset{\rightarrow} {{r}}\right)=\mathrm{0} \\ $$$$\Rightarrow\overset{\rightarrow} {{p}}\bot\delta\overset{\rightarrow} {{p}}\parallel\overset{\rightarrow} {{q}}−\overset{\rightarrow} {{r}}\Rightarrow\overset{\rightarrow} {{p}}\bot\left(\overset{\rightarrow} {{q}}−\overset{\rightarrow} {{r}}\right) \\ $$$${But}\:\left(\overset{\rightarrow} {{q}}−\overset{\rightarrow} {{r}}\right)\:{is}\:{the}\:{side}\:{of}\:{the}\:{triangle} \\ $$$${opposite}\:{the}\:{vertex}\:{defined}\:{by}\:\overset{\rightarrow} {{p}}. \\ $$$$\Rightarrow\overset{\rightarrow} {{p}}\:{must}\:{be}\:{colinear}\:{to}\:{the}\:{height} \\ $$$${This}\:{must}\:{be}\:{true}\:{for}\:\overset{\rightarrow} {{q}}\:{and}\:\overset{\rightarrow} {{r}}\:{too}. \\ $$$$\Rightarrow\:{The}\:{starting}\:{point}\:{is}\:{the}\:{orthocenter}. \\ $$

Commented by papa last updated on 04/May/22

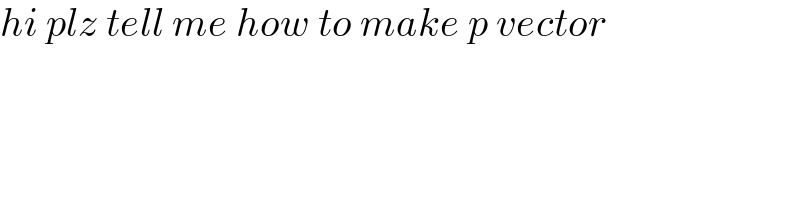
$${hi}\:{plz}\:{tell}\:{me}\:{how}\:{to}\:{make}\:{p}\:{vector} \\ $$

Commented by mr W last updated on 04/May/22

Commented by mr W last updated on 04/May/22

Answered by mr W last updated on 27/Dec/21

Commented by mr W last updated on 27/Dec/21

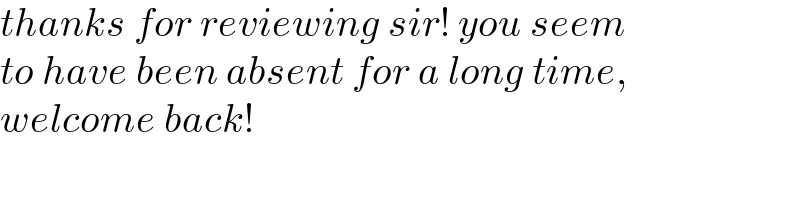
$${thanks}\:{for}\:{reviewing}\:{sir}!\:{you}\:{seem} \\ $$$${to}\:{have}\:{been}\:{absent}\:{for}\:{a}\:{long}\:{time}, \\ $$$${welcome}\:{back}! \\ $$

Commented by mr W last updated on 27/Dec/21

the area of ABC is Δ=(1/2)(pq sin α+qr sin β+rp sin γ) α+β+γ=2π Δ=(1/2)[pq sin α+qr sin β−rp sin (α+β)] such that Δ is maximum, (∂Δ/∂α)=(1/2)[pq cos α−rp cos (α+β)]=0 ⇒pq cos α=rp cos (α+β)=rp cos γ (∂Δ/∂β)=(1/2)[qr cos β−rp cos (α+β)]=0 ⇒qr cos β=rp cos (α+β)=rp cos γ so we have pq cos α=qr cos β=rp cos γ=k say cos α=(k/(pq)) ⇒sin α=(√(1−(k^2 /(p^2 q^2 )))) cos β=(k/(qr)) ⇒sin β=(√(1−(k^2 /(q^2 r^2 )))) cos γ=(k/(rp)) ⇒sin γ=(√(1−(k^2 /(r^2 p^2 )))) k−rp [(k^2 /(pq^2 r))−(√((1−(k^2 /(p^2 q^2 )))(1−(k^2 /(q^2 r^2 )))))]=0 (√((p^2 q^2 −k^2 )(q^2 r^2 −k^2 )))=k^2 −q^2 k p^2 q^4 r^2 −(p^2 q^2 +q^2 r^2 )k^2 +k^4 =k^4 +q^4 k^2 −2q^2 k^3 p^2 q^2 r^2 −(p^2 +q^2 +r^2 )k^2 +2k^3 =0 determinant ((((1/k^3 )−(((p^2 +q^2 +r^2 )/(p^2 q^2 r^2 )))(1/k)+(2/(p^2 q^2 r^2 ))=0))) p^2 q^2 r^2 −(1/(27))(p^2 +q^2 +r^2 )^3 ≤0 ⇒three roots (1/k)=(2/(pqr))(√((p^2 +q^2 +r^2 )/3)) sin {((2nπ)/3)+(1/3) sin^(−1) pqr((3/(p^2 +q^2 +r^2 )))^(3/2) } (n=0,1,2) but suitable for maximum Δ is only the root with n=2: determinant ((((1/k)=−(2/(pqr))(√((p^2 +q^2 +r^2 )/3)) sin {(π/3)+(1/3) sin^(−1) pqr((3/(p^2 +q^2 +r^2 )))^(3/2) }))) Δ_(max) =(1/2)((√(p^2 q^2 −k^2 ))+(√(q^2 r^2 −k^2 ))+(√(r^2 p^2 −k^2 ))) a^2 =q^2 +r^2 −2qr cos β=q^2 +r^2 −2k a=(√(q^2 +r^2 −2k)) b=(√(r^2 +p^2 −2k)) c=(√(p^2 +q^2 −2k)) example: p=10, q=8, r=4 Δ_(max) ≈67.303409 a≈11.084677 b≈12.604367 c≈14.382978 coresponding equilateral triangle: s≈11.943609, Δ≈61.769169

$${the}\:{area}\:{of}\:{ABC}\:{is} \\ $$$$\Delta=\frac{\mathrm{1}}{\mathrm{2}}\left({pq}\:\mathrm{sin}\:\alpha+{qr}\:\mathrm{sin}\:\beta+{rp}\:\mathrm{sin}\:\gamma\right) \\ $$$$\alpha+\beta+\gamma=\mathrm{2}\pi \\ $$$$\Delta=\frac{\mathrm{1}}{\mathrm{2}}\left[{pq}\:\mathrm{sin}\:\alpha+{qr}\:\mathrm{sin}\:\beta−{rp}\:\mathrm{sin}\:\left(\alpha+\beta\right)\right] \\ $$$${such}\:{that}\:\Delta\:{is}\:{maximum}, \\ $$$$\frac{\partial\Delta}{\partial\alpha}=\frac{\mathrm{1}}{\mathrm{2}}\left[{pq}\:\mathrm{cos}\:\alpha−{rp}\:\mathrm{cos}\:\left(\alpha+\beta\right)\right]=\mathrm{0} \\ $$$$\Rightarrow{pq}\:\mathrm{cos}\:\alpha={rp}\:\mathrm{cos}\:\left(\alpha+\beta\right)={rp}\:\mathrm{cos}\:\gamma \\ $$$$\frac{\partial\Delta}{\partial\beta}=\frac{\mathrm{1}}{\mathrm{2}}\left[{qr}\:\mathrm{cos}\:\beta−{rp}\:\mathrm{cos}\:\left(\alpha+\beta\right)\right]=\mathrm{0} \\ $$$$\Rightarrow{qr}\:\mathrm{cos}\:\beta={rp}\:\mathrm{cos}\:\left(\alpha+\beta\right)={rp}\:\mathrm{cos}\:\gamma \\ $$$$ \\ $$$${so}\:{we}\:{have} \\ $$$${pq}\:\mathrm{cos}\:\alpha={qr}\:\mathrm{cos}\:\beta={rp}\:\mathrm{cos}\:\gamma={k}\:{say} \\ $$$$\mathrm{cos}\:\alpha=\frac{{k}}{{pq}}\:\Rightarrow\mathrm{sin}\:\alpha=\sqrt{\mathrm{1}−\frac{{k}^{\mathrm{2}} }{{p}^{\mathrm{2}} {q}^{\mathrm{2}} }} \\ $$$$\mathrm{cos}\:\beta=\frac{{k}}{{qr}}\:\Rightarrow\mathrm{sin}\:\beta=\sqrt{\mathrm{1}−\frac{{k}^{\mathrm{2}} }{{q}^{\mathrm{2}} {r}^{\mathrm{2}} }} \\ $$$$\mathrm{cos}\:\gamma=\frac{{k}}{{rp}}\:\Rightarrow\mathrm{sin}\:\gamma=\sqrt{\mathrm{1}−\frac{{k}^{\mathrm{2}} }{{r}^{\mathrm{2}} {p}^{\mathrm{2}} }} \\ $$$${k}−{rp}\:\left[\frac{{k}^{\mathrm{2}} }{{pq}^{\mathrm{2}} {r}}−\sqrt{\left(\mathrm{1}−\frac{{k}^{\mathrm{2}} }{{p}^{\mathrm{2}} {q}^{\mathrm{2}} }\right)\left(\mathrm{1}−\frac{{k}^{\mathrm{2}} }{{q}^{\mathrm{2}} {r}^{\mathrm{2}} }\right)}\right]=\mathrm{0} \\ $$$$\sqrt{\left({p}^{\mathrm{2}} {q}^{\mathrm{2}} −{k}^{\mathrm{2}} \right)\left({q}^{\mathrm{2}} {r}^{\mathrm{2}} −{k}^{\mathrm{2}} \right)}={k}^{\mathrm{2}} −{q}^{\mathrm{2}} {k} \\ $$$${p}^{\mathrm{2}} {q}^{\mathrm{4}} {r}^{\mathrm{2}} −\left({p}^{\mathrm{2}} {q}^{\mathrm{2}} +{q}^{\mathrm{2}} {r}^{\mathrm{2}} \right){k}^{\mathrm{2}} +{k}^{\mathrm{4}} ={k}^{\mathrm{4}} +{q}^{\mathrm{4}} {k}^{\mathrm{2}} −\mathrm{2}{q}^{\mathrm{2}} {k}^{\mathrm{3}} \\ $$$${p}^{\mathrm{2}} {q}^{\mathrm{2}} {r}^{\mathrm{2}} −\left({p}^{\mathrm{2}} +{q}^{\mathrm{2}} +{r}^{\mathrm{2}} \right){k}^{\mathrm{2}} +\mathrm{2}{k}^{\mathrm{3}} =\mathrm{0} \\ $$$$\begin{array}{|c|}{\frac{\mathrm{1}}{{k}^{\mathrm{3}} }−\left(\frac{{p}^{\mathrm{2}} +{q}^{\mathrm{2}} +{r}^{\mathrm{2}} }{{p}^{\mathrm{2}} {q}^{\mathrm{2}} {r}^{\mathrm{2}} }\right)\frac{\mathrm{1}}{{k}}+\frac{\mathrm{2}}{{p}^{\mathrm{2}} {q}^{\mathrm{2}} {r}^{\mathrm{2}} }=\mathrm{0}}\\\hline\end{array} \\ $$$${p}^{\mathrm{2}} {q}^{\mathrm{2}} {r}^{\mathrm{2}} −\frac{\mathrm{1}}{\mathrm{27}}\left({p}^{\mathrm{2}} +{q}^{\mathrm{2}} +{r}^{\mathrm{2}} \right)^{\mathrm{3}} \leqslant\mathrm{0}\:\Rightarrow{three}\:{roots} \\ $$$$\frac{\mathrm{1}}{{k}}=\frac{\mathrm{2}}{{pqr}}\sqrt{\frac{{p}^{\mathrm{2}} +{q}^{\mathrm{2}} +{r}^{\mathrm{2}} }{\mathrm{3}}}\:\mathrm{sin}\:\left\{\frac{\mathrm{2}{n}\pi}{\mathrm{3}}+\frac{\mathrm{1}}{\mathrm{3}}\:\mathrm{sin}^{−\mathrm{1}} \:{pqr}\left(\frac{\mathrm{3}}{{p}^{\mathrm{2}} +{q}^{\mathrm{2}} +{r}^{\mathrm{2}} }\right)^{\frac{\mathrm{3}}{\mathrm{2}}} \right\}\:\:\left({n}=\mathrm{0},\mathrm{1},\mathrm{2}\right) \\ $$$${but}\:{suitable}\:{for}\:{maximum}\:\Delta\:{is}\:{only}\: \\ $$$${the}\:{root}\:{with}\:{n}=\mathrm{2}: \\ $$$$\begin{array}{|c|}{\frac{\mathrm{1}}{{k}}=−\frac{\mathrm{2}}{{pqr}}\sqrt{\frac{{p}^{\mathrm{2}} +{q}^{\mathrm{2}} +{r}^{\mathrm{2}} }{\mathrm{3}}}\:\mathrm{sin}\:\left\{\frac{\pi}{\mathrm{3}}+\frac{\mathrm{1}}{\mathrm{3}}\:\mathrm{sin}^{−\mathrm{1}} \:{pqr}\left(\frac{\mathrm{3}}{{p}^{\mathrm{2}} +{q}^{\mathrm{2}} +{r}^{\mathrm{2}} }\right)^{\frac{\mathrm{3}}{\mathrm{2}}} \right\}}\\\hline\end{array} \\ $$$$ \\ $$$$\Delta_{{max}} =\frac{\mathrm{1}}{\mathrm{2}}\left(\sqrt{{p}^{\mathrm{2}} {q}^{\mathrm{2}} −{k}^{\mathrm{2}} }+\sqrt{{q}^{\mathrm{2}} {r}^{\mathrm{2}} −{k}^{\mathrm{2}} }+\sqrt{{r}^{\mathrm{2}} {p}^{\mathrm{2}} −{k}^{\mathrm{2}} }\right) \\ $$$${a}^{\mathrm{2}} ={q}^{\mathrm{2}} +{r}^{\mathrm{2}} −\mathrm{2}{qr}\:\mathrm{cos}\:\beta={q}^{\mathrm{2}} +{r}^{\mathrm{2}} −\mathrm{2}{k} \\ $$$${a}=\sqrt{{q}^{\mathrm{2}} +{r}^{\mathrm{2}} −\mathrm{2}{k}} \\ $$$${b}=\sqrt{{r}^{\mathrm{2}} +{p}^{\mathrm{2}} −\mathrm{2}{k}} \\ $$$${c}=\sqrt{{p}^{\mathrm{2}} +{q}^{\mathrm{2}} −\mathrm{2}{k}} \\ $$$$ \\ $$$$\underline{{example}:\:{p}=\mathrm{10},\:{q}=\mathrm{8},\:{r}=\mathrm{4}} \\ $$$$\Delta_{{max}} \approx\mathrm{67}.\mathrm{303409} \\ $$$${a}\approx\mathrm{11}.\mathrm{084677} \\ $$$${b}\approx\mathrm{12}.\mathrm{604367} \\ $$$${c}\approx\mathrm{14}.\mathrm{382978} \\ $$$${coresponding}\:{equilateral}\:{triangle}: \\ $$$${s}\approx\mathrm{11}.\mathrm{943609},\:\Delta\approx\mathrm{61}.\mathrm{769169} \\ $$

Commented by mr W last updated on 27/Dec/21

Commented by mr W last updated on 27/Dec/21

Commented by mr W last updated on 27/Dec/21

Commented by mr W last updated on 27/Dec/21

Commented by mr W last updated on 27/Dec/21

we see generally the coresponding equilateral triangle (blue marked in diagrams) (see also Q123040) is not the triangle with the maximum area.

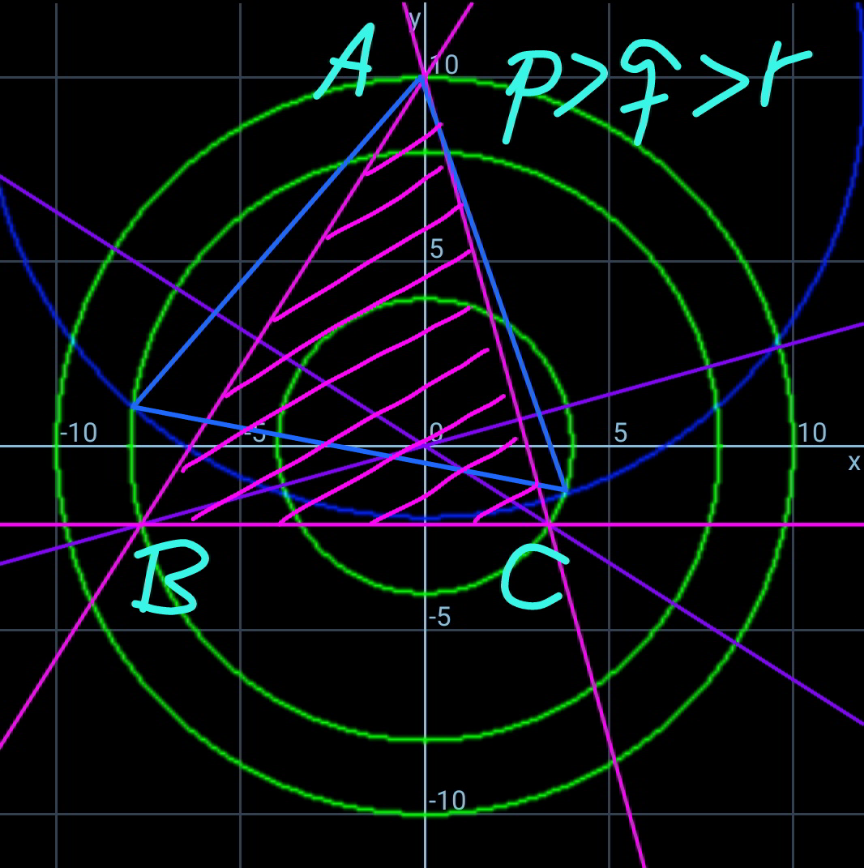
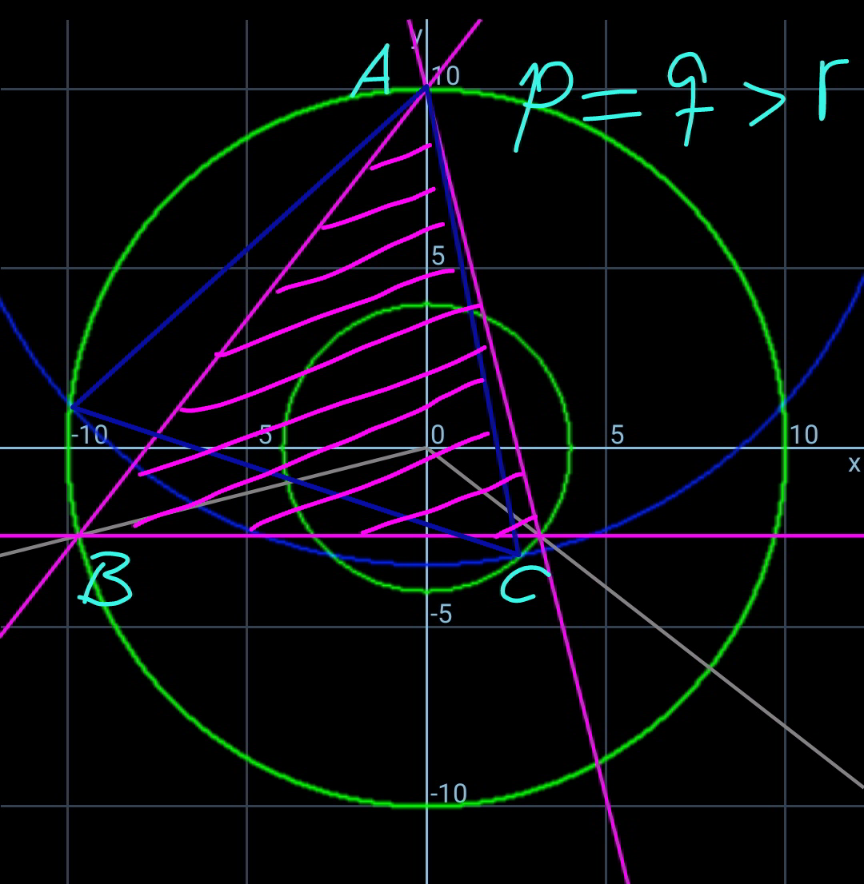
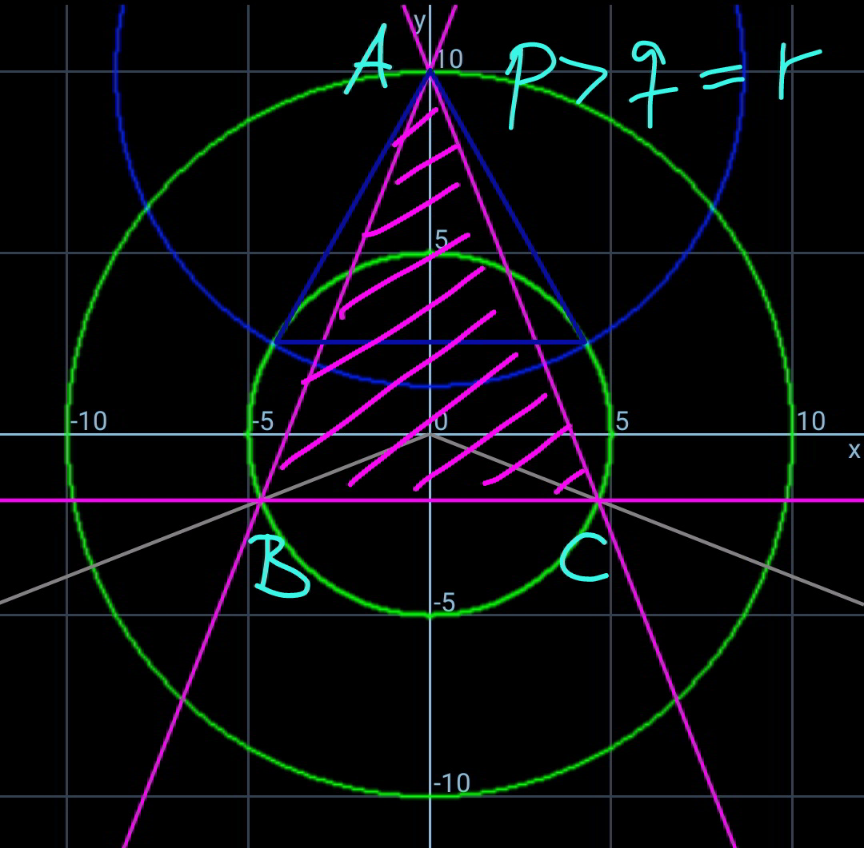
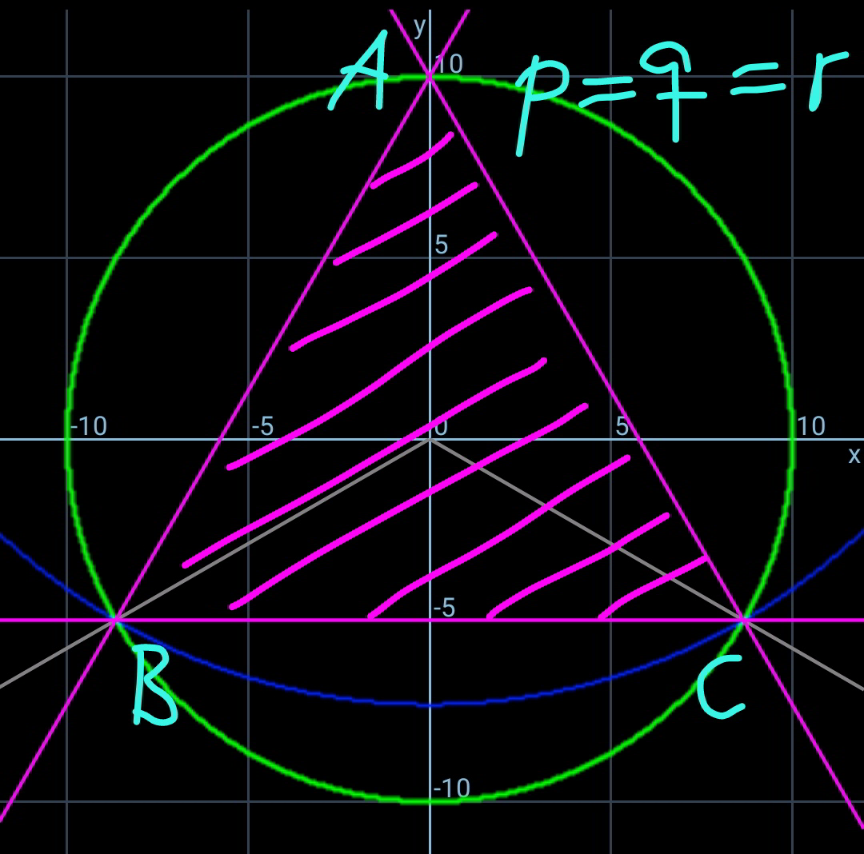
$${we}\:{see}\:{generally}\:{the}\:{coresponding} \\ $$$${equilateral}\:{triangle}\:\left({blue}\:{marked}\:{in}\right. \\ $$$$\left.{diagrams}\right)\:\left({see}\:{also}\:{Q}\mathrm{123040}\right)\:{is}\:{not} \\ $$$${the}\:{triangle}\:{with}\:{the}\:{maximum}\: \\ $$$${area}. \\ $$

Commented by mr W last updated on 27/Dec/21

from pq cos α=qr cos β=rp cos γ we get q cos α=r cos γ, that means AO⊥BC. similarly BO⊥CA, CO⊥AB. that means O is the orthocenter of triangle ABC when the triangle has the maximum area. example: p=7, q=6, r=5 a≈9.7924505 b≈10.4351372 c≈10.9495245 this is the same result as in Q161015.

$${from}\:{pq}\:\mathrm{cos}\:\alpha={qr}\:\mathrm{cos}\:\beta={rp}\:\mathrm{cos}\:\gamma \\ $$$${we}\:{get}\:{q}\:\mathrm{cos}\:\alpha={r}\:\mathrm{cos}\:\gamma,\:{that}\:{means} \\ $$$${AO}\bot{BC}.\:{similarly}\:{BO}\bot{CA},\:{CO}\bot{AB}. \\ $$$${that}\:{means}\:{O}\:{is}\:{the}\:{orthocenter}\:{of} \\ $$$${triangle}\:{ABC}\:{when}\:{the}\:{triangle} \\ $$$${has}\:{the}\:{maximum}\:{area}. \\ $$$${example}:\:{p}=\mathrm{7},\:{q}=\mathrm{6},\:{r}=\mathrm{5} \\ $$$${a}\approx\mathrm{9}.\mathrm{7924505} \\ $$$${b}\approx\mathrm{10}.\mathrm{4351372} \\ $$$${c}\approx\mathrm{10}.\mathrm{9495245} \\ $$$${this}\:{is}\:{the}\:{same}\:{result}\:{as}\:{in}\:{Q}\mathrm{161015}. \\ $$

Commented by Tawa11 last updated on 27/Dec/21

$$\mathrm{Great}\:\mathrm{sir}. \\ $$

Commented by behi834171 last updated on 27/Dec/21

$${greaaaaaaaaaat}\:{dear}\:{master}. \\ $$$${thanks}\:{a}\:{lot}. \\ $$

Commented by behi834171 last updated on 27/Dec/21

$$ \\ $$Thank you so much,dear master,for your favor.
I'm here,from now on.

Commented by behi834171 last updated on 27/Dec/21

$$\gamma=\mathrm{90}^{\bullet} \:{is}\:{an}\:\:{interesting}\:{case}.{I}\:{think}. \\ $$

Commented by mr W last updated on 27/Dec/21

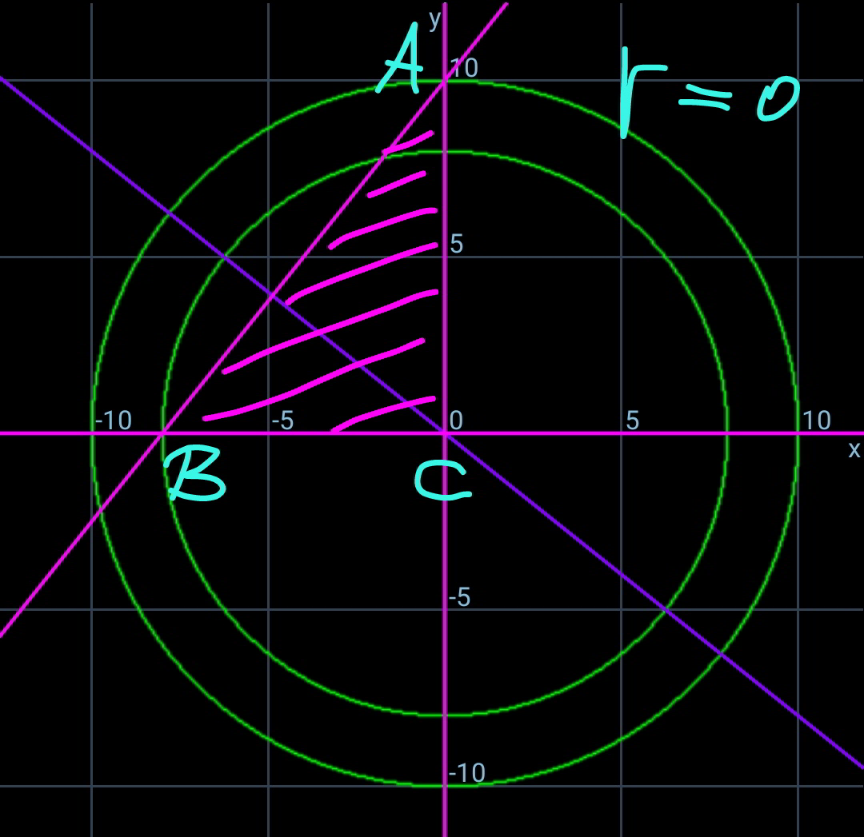
$${when}\:{one}\:{of}\:{p},{q},{r}\:{is}\:{zero},\:{then}\:{the} \\ $$$${coresponding}\:{vertex}\:{is}\:{also}\:{the} \\ $$$${orthocenter}.\:{in}\:{this}\:{case}\:{the}\:{triangle} \\ $$$${is}\:{right}\:{angled}. \\ $$

Commented by mr W last updated on 27/Dec/21

Commented by behi834171 last updated on 27/Dec/21

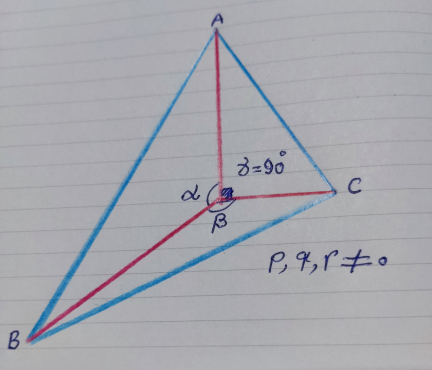
Commented by behi834171 last updated on 27/Dec/21

$$\gamma=\mathrm{90}^{\bullet} ,{p},{q},{r}\neq\mathrm{0} \\ $$

Commented by mr W last updated on 27/Dec/21

the task here is to find the triangle with maximum area when p,q,r are given. it is not to find the triangle with given α,β or γ. so far as p,q,r≠0, the triangle with maxixum area can never be a triangle with γ=90° ! the triangle you gave with γ=90° is not the triangle which has the maximum area.

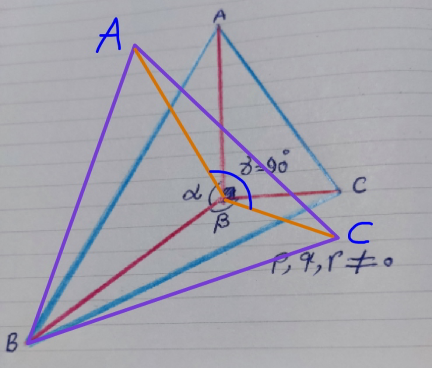
$${the}\:{task}\:{here}\:{is}\:{to}\:{find}\:{the}\:{triangle} \\ $$$${with}\:{maximum}\:{area}\:{when}\:{p},{q},{r}\:{are} \\ $$$${given}.\:{it}\:{is}\:{not}\:{to}\:{find}\:{the}\:{triangle} \\ $$$${with}\:{given}\:\alpha,\beta\:{or}\:\gamma.\: \\ $$$${so}\:{far}\:{as}\:{p},{q},{r}\neq\mathrm{0},\:{the}\:{triangle}\:{with}\: \\ $$$${maxixum}\:{area}\:{can}\:{never}\:{be}\:{a}\:{triangle} \\ $$$${with}\:\gamma=\mathrm{90}°\:! \\ $$$${the}\:{triangle}\:{you}\:{gave}\:{with}\:\gamma=\mathrm{90}°\:{is} \\ $$$${not}\:{the}\:{triangle}\:{which}\:{has}\:{the} \\ $$$${maximum}\:{area}. \\ $$

Commented by mr W last updated on 27/Dec/21

Commented by behi834171 last updated on 27/Dec/21

thank you very much for your attention. can we find the sides of such triangle whit:γ=90^• ? i have the such unsolved problem in forum but i don′t remember its q.ID...

$${thank}\:{you}\:{very}\:{much}\:{for}\:{your}\:{attention}. \\ $$$${can}\:{we}\:{find}\:{the}\:{sides}\:{of}\:{such}\:{triangle} \\ $$$${whit}:\gamma=\mathrm{90}^{\bullet} \:? \\ $$$${i}\:{have}\:{the}\:{such}\:{unsolved}\:{problem}\:{in}\:{forum} \\ $$$${but}\:{i}\:{don}'{t}\:{remember}\:{its}\:{q}.{ID}… \\ $$

Commented by mr W last updated on 27/Dec/21

$${you}\:{must}\:{specify}\:{exactly}\:{what}\:{is}\:{your} \\ $$$${task}.\:{in}\:{the}\:{current}\:{question}\:{the} \\ $$$${point}\:{O}\:{is}\:{the}\:{orthocenter}\:{of}\:{the} \\ $$$${triangle}.\:{we}\:{can}\:{not}\:{find}\:{a}\:{triangle} \\ $$$${whose}\:{orthocenter}\:{lies}\:{inside}\:{the} \\ $$$${triangle}\:{and}\:{makes}\:{an}\:{angle}\:\gamma=\mathrm{90}°. \\ $$$${this}\:{is}\:{only}\:{the}\:{case}\:{when}\:{the}\: \\ $$$${orthocenter}\:{lies}\:{at}\:{one}\:{vertex}\:{of}\:{a} \\ $$$${right}\:{angled}\:{triangle},\:{but}\:{in}\:{this} \\ $$$${case}\:{one}\:{of}\:{p},{q},{r}\:{is}\:{zero}. \\ $$

Commented by behi834171 last updated on 27/Dec/21

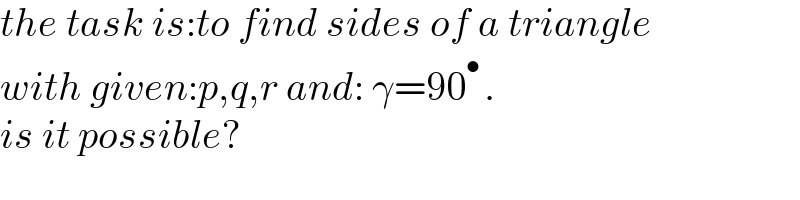
the task is:to find sides of a triangle with given:p,q,r and: γ=90^(• ) . is it possible?

$${the}\:{task}\:{is}:{to}\:{find}\:{sides}\:{of}\:{a}\:{triangle} \\ $$$${with}\:{given}:{p},{q},{r}\:{and}:\:\gamma=\mathrm{90}^{\bullet\:} . \\ $$$${is}\:{it}\:{possible}? \\ $$

Commented by mr W last updated on 27/Dec/21