Question Number 31003 by rahul 19 last updated on 01/Mar/18
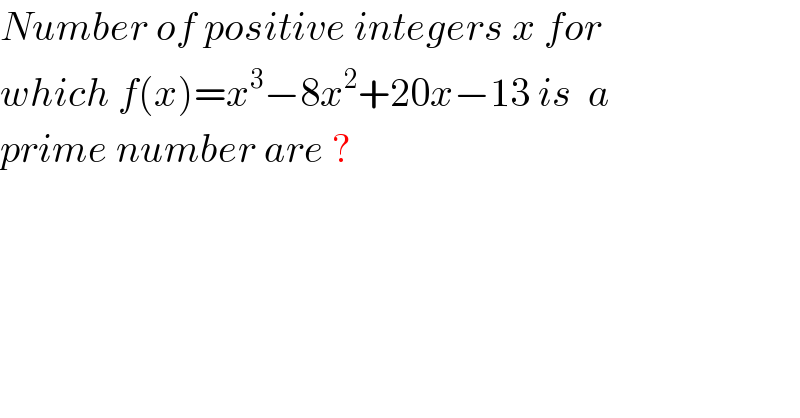
$${Number}\:{of}\:{positive}\:{integers}\:{x}\:{for} \\ $$$${which}\:{f}\left({x}\right)={x}^{\mathrm{3}} −\mathrm{8}{x}^{\mathrm{2}} +\mathrm{20}{x}−\mathrm{13}\:{is}\:\:{a}\: \\ $$$${prime}\:{number}\:{are}\:? \\ $$
Answered by MJS last updated on 07/Mar/18
![f(x)=(x−z_1 )(x−z_2 )(x−z_3 ) this can only be prime if only one of the brackets contain a prime number, and the two others are worth 1 or −1 so we need the zeros of f(x) z_1 z_2 z_3 =13, so let′s try x=±1 or x=±13 f(1)=0 f(x)=(x−1)(x^2 −7x+13) [x^2 −7x+13=0 (7/2)±(√(((49)/4)−13))=(7/2)±(√(−(3/4))) no solution ∈R] so (x−1)=±1 ∧ (x^2 −7x+13) is prime or (x−1) is prime ∧ (x^2 −7x+13)=±1 x−1=1 ⇒ x=2 2^2 −7∙2+13=3 ⇒ f(2) is prime x−1=−1 ⇒ x=0 0^2 −7∙0+13=13 ⇒ f(0) is prime but x must be a positive integer x^2 −7x+13=1 (7/2)±(√(((49)/4)−12))=(7/2)±(1/2) x_1 =3; (3−1)=2 ⇒ f(3) is prime x_2 =4; (4−1)=3 ⇒ f(4) is prime x^2 −7x+13=−1 has no solution ∈R number of positive integers is 3](https://www.tinkutara.com/question/Q31013.png)
$${f}\left({x}\right)=\left({x}−{z}_{\mathrm{1}} \right)\left({x}−{z}_{\mathrm{2}} \right)\left({x}−{z}_{\mathrm{3}} \right) \\ $$$$\mathrm{this}\:\mathrm{can}\:\mathrm{only}\:\mathrm{be}\:\mathrm{prime}\:\mathrm{if}\:\mathrm{only}\:\mathrm{one} \\ $$$$\mathrm{of}\:\mathrm{the}\:\mathrm{brackets}\:\mathrm{contain}\:\mathrm{a}\:\mathrm{prime} \\ $$$$\mathrm{number},\:\mathrm{and}\:\mathrm{the}\:\mathrm{two}\:\mathrm{others}\:\mathrm{are} \\ $$$$\mathrm{worth}\:\mathrm{1}\:\mathrm{or}\:−\mathrm{1} \\ $$$$\mathrm{so}\:\mathrm{we}\:\mathrm{need}\:\mathrm{the}\:\mathrm{zeros}\:\mathrm{of}\:{f}\left({x}\right) \\ $$$${z}_{\mathrm{1}} {z}_{\mathrm{2}} {z}_{\mathrm{3}} =\mathrm{13},\:\mathrm{so}\:\mathrm{let}'\mathrm{s}\:\mathrm{try} \\ $$$${x}=\pm\mathrm{1}\:\mathrm{or}\:{x}=\pm\mathrm{13} \\ $$$${f}\left(\mathrm{1}\right)=\mathrm{0} \\ $$$${f}\left({x}\right)=\left({x}−\mathrm{1}\right)\left({x}^{\mathrm{2}} −\mathrm{7}{x}+\mathrm{13}\right) \\ $$$$\left[{x}^{\mathrm{2}} −\mathrm{7}{x}+\mathrm{13}=\mathrm{0}\right. \\ $$$$\frac{\mathrm{7}}{\mathrm{2}}\pm\sqrt{\frac{\mathrm{49}}{\mathrm{4}}−\mathrm{13}}=\frac{\mathrm{7}}{\mathrm{2}}\pm\sqrt{−\frac{\mathrm{3}}{\mathrm{4}}} \\ $$$$\left.\mathrm{no}\:\mathrm{solution}\:\in\mathbb{R}\right] \\ $$$$ \\ $$$$\mathrm{so}\:\left({x}−\mathrm{1}\right)=\pm\mathrm{1}\:\wedge\:\left({x}^{\mathrm{2}} −\mathrm{7}{x}+\mathrm{13}\right)\:\mathrm{is}\:\mathrm{prime} \\ $$$$\mathrm{or}\:\left({x}−\mathrm{1}\right)\:\mathrm{is}\:\mathrm{prime}\:\wedge\:\left({x}^{\mathrm{2}} −\mathrm{7}{x}+\mathrm{13}\right)=\pm\mathrm{1} \\ $$$$ \\ $$$${x}−\mathrm{1}=\mathrm{1}\:\Rightarrow\:\:{x}=\mathrm{2} \\ $$$$\mathrm{2}^{\mathrm{2}} −\mathrm{7}\centerdot\mathrm{2}+\mathrm{13}=\mathrm{3}\:\Rightarrow\:{f}\left(\mathrm{2}\right)\:\mathrm{is}\:\mathrm{prime} \\ $$$${x}−\mathrm{1}=−\mathrm{1}\:\Rightarrow\:{x}=\mathrm{0} \\ $$$$\mathrm{0}^{\mathrm{2}} −\mathrm{7}\centerdot\mathrm{0}+\mathrm{13}=\mathrm{13}\:\Rightarrow\:{f}\left(\mathrm{0}\right)\:\mathrm{is}\:\mathrm{prime} \\ $$$$\mathrm{but}\:{x}\:\mathrm{must}\:\mathrm{be}\:\mathrm{a}\:\mathrm{positive}\:\mathrm{integer} \\ $$$$ \\ $$$${x}^{\mathrm{2}} −\mathrm{7}{x}+\mathrm{13}=\mathrm{1} \\ $$$$\frac{\mathrm{7}}{\mathrm{2}}\pm\sqrt{\frac{\mathrm{49}}{\mathrm{4}}−\mathrm{12}}=\frac{\mathrm{7}}{\mathrm{2}}\pm\frac{\mathrm{1}}{\mathrm{2}} \\ $$$${x}_{\mathrm{1}} =\mathrm{3};\:\left(\mathrm{3}−\mathrm{1}\right)=\mathrm{2}\:\Rightarrow\:{f}\left(\mathrm{3}\right)\:\mathrm{is}\:\mathrm{prime} \\ $$$${x}_{\mathrm{2}} =\mathrm{4};\:\left(\mathrm{4}−\mathrm{1}\right)=\mathrm{3}\:\Rightarrow\:{f}\left(\mathrm{4}\right)\:\mathrm{is}\:\mathrm{prime} \\ $$$$ \\ $$$${x}^{\mathrm{2}} −\mathrm{7}{x}+\mathrm{13}=−\mathrm{1} \\ $$$$\mathrm{has}\:\mathrm{no}\:\mathrm{solution}\:\in\mathbb{R} \\ $$$$ \\ $$$$\mathrm{number}\:\mathrm{of}\:\mathrm{positive}\:\mathrm{integers}\:\mathrm{is}\:\mathrm{3} \\ $$
