Question Number 31095 by abdo imad last updated on 02/Mar/18
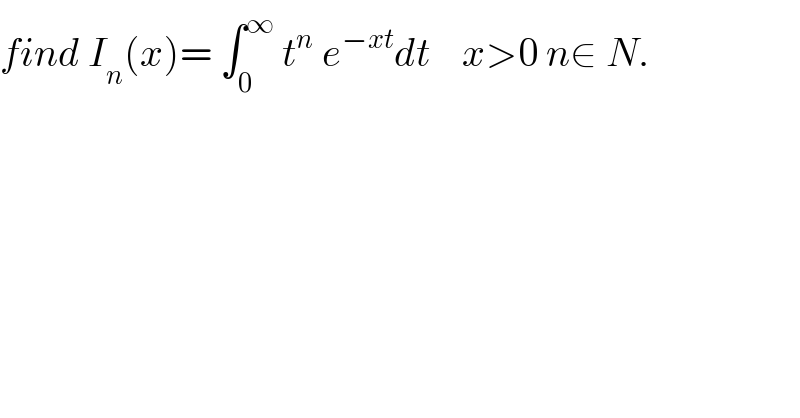
$${find}\:{I}_{{n}} \left({x}\right)=\:\int_{\mathrm{0}} ^{\infty} \:{t}^{{n}} \:{e}^{−{xt}} {dt}\:\:\:\:{x}>\mathrm{0}\:{n}\in\:{N}. \\ $$
Commented by abdo imad last updated on 04/Mar/18
![ch.xt=u give I_n (x)=∫_0 ^∞ ((u/x))^n e^(−u) (du/x) =(1/x^(n+1) )∫_0 ^∞ u^n e^(−u) du let put A_n =∫_0 ^∞ u^n e^(−u) du by parts A_n =[−u^n e^(−u) ]_0 ^∞ +∫_0 ^∞ n u^(n−1) e^(−u) du=nA_(n−1) ⇒ Π_(k=1) ^n A_k =n! Π_(k=1) ^n A_(k−1) ⇒A_n =n!A_0 =n!( A_0 =1)⇒ I_n (x)=((n!)/x^(n+1) ) .](https://www.tinkutara.com/question/Q31267.png)
$${ch}.{xt}={u}\:{give}\:{I}_{{n}} \left({x}\right)=\int_{\mathrm{0}} ^{\infty} \left(\frac{{u}}{{x}}\right)^{{n}} \:{e}^{−{u}} \:\frac{{du}}{{x}} \\ $$$$=\frac{\mathrm{1}}{{x}^{{n}+\mathrm{1}} }\int_{\mathrm{0}} ^{\infty} \:{u}^{{n}} \:{e}^{−{u}} {du}\:{let}\:{put}\:{A}_{{n}} =\int_{\mathrm{0}} ^{\infty} \:{u}^{{n}} \:{e}^{−{u}} {du}\:\:{by}\:{parts} \\ $$$${A}_{{n}} =\left[−{u}^{{n}} {e}^{−{u}} \right]_{\mathrm{0}} ^{\infty} \:+\int_{\mathrm{0}} ^{\infty} {n}\:{u}^{{n}−\mathrm{1}} \:{e}^{−{u}} {du}={nA}_{{n}−\mathrm{1}} \:\Rightarrow \\ $$$$\prod_{{k}=\mathrm{1}} ^{{n}} {A}_{{k}} ={n}!\:\prod_{{k}=\mathrm{1}} ^{{n}} {A}_{{k}−\mathrm{1}} \:\:\Rightarrow{A}_{{n}} ={n}!{A}_{\mathrm{0}} \:={n}!\left(\:\:{A}_{\mathrm{0}} =\mathrm{1}\right)\Rightarrow \\ $$$${I}_{{n}} \left({x}\right)=\frac{{n}!}{{x}^{{n}+\mathrm{1}} }\:. \\ $$
