Question Number 96660 by mathmax by abdo last updated on 03/Jun/20
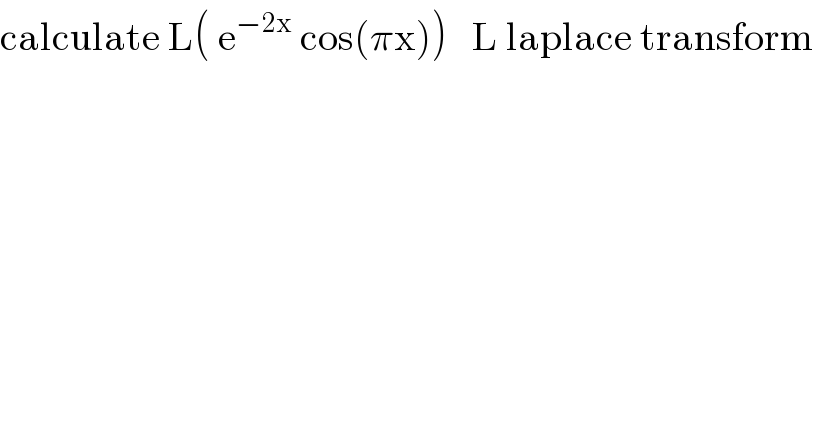
$$\mathrm{calculate}\:\mathrm{L}\left(\:\mathrm{e}^{−\mathrm{2x}} \:\mathrm{cos}\left(\pi\mathrm{x}\right)\right)\:\:\:\mathrm{L}\:\mathrm{laplace}\:\mathrm{transform} \\ $$
Answered by mathmax by abdo last updated on 04/Jun/20
![L(e^(−2x) cos(πx)) =∫_0 ^∞ e^(−2t) cos(πt)e^(−xt) dt =∫_0 ^∞ e^(−(x+2)t) cos(πt)dt =Re(∫_0 ^∞ e^(−(x+2)t) e^(iπt) dt) =Re(∫_0 ^∞ e^((−x−2 +iπ)t) dt) we have ∫_0 ^∞ e^((−x−2 +iπ)t) dt =[(1/(−x−2+iπ)) e^((−x−2+iπ)t) ]_0 ^(+∞) =−(1/(−x−2+iπ)) =(1/(x+2−iπ)) =((x+2 +iπ)/((x+2)^2 +π^2 )) ⇒ L(e^(−2x) cos(πx)) =((x+2)/((x+2)^2 +π^2 ))](https://www.tinkutara.com/question/Q96702.png)
$$\mathrm{L}\left(\mathrm{e}^{−\mathrm{2x}} \:\mathrm{cos}\left(\pi\mathrm{x}\right)\right)\:=\int_{\mathrm{0}} ^{\infty} \:\mathrm{e}^{−\mathrm{2t}} \:\mathrm{cos}\left(\pi\mathrm{t}\right)\mathrm{e}^{−\mathrm{xt}} \:\mathrm{dt} \\ $$$$=\int_{\mathrm{0}} ^{\infty} \:\:\mathrm{e}^{−\left(\mathrm{x}+\mathrm{2}\right)\mathrm{t}} \:\mathrm{cos}\left(\pi\mathrm{t}\right)\mathrm{dt}\:=\mathrm{Re}\left(\int_{\mathrm{0}} ^{\infty} \:\mathrm{e}^{−\left(\mathrm{x}+\mathrm{2}\right)\mathrm{t}} \:\mathrm{e}^{\mathrm{i}\pi\mathrm{t}} \mathrm{dt}\right) \\ $$$$=\mathrm{Re}\left(\int_{\mathrm{0}} ^{\infty} \:\mathrm{e}^{\left(−\mathrm{x}−\mathrm{2}\:+\mathrm{i}\pi\right)\mathrm{t}} \mathrm{dt}\right)\:\mathrm{we}\:\mathrm{have} \\ $$$$\int_{\mathrm{0}} ^{\infty} \:\mathrm{e}^{\left(−\mathrm{x}−\mathrm{2}\:+\mathrm{i}\pi\right)\mathrm{t}} \:\mathrm{dt}\:=\left[\frac{\mathrm{1}}{−\mathrm{x}−\mathrm{2}+\mathrm{i}\pi}\:\:\mathrm{e}^{\left(−\mathrm{x}−\mathrm{2}+\mathrm{i}\pi\right)\mathrm{t}} \right]_{\mathrm{0}} ^{+\infty} \\ $$$$=−\frac{\mathrm{1}}{−\mathrm{x}−\mathrm{2}+\mathrm{i}\pi}\:=\frac{\mathrm{1}}{\mathrm{x}+\mathrm{2}−\mathrm{i}\pi}\:=\frac{\mathrm{x}+\mathrm{2}\:+\mathrm{i}\pi}{\left(\mathrm{x}+\mathrm{2}\right)^{\mathrm{2}} +\pi^{\mathrm{2}} }\:\Rightarrow \\ $$$$\mathrm{L}\left(\mathrm{e}^{−\mathrm{2x}} \:\mathrm{cos}\left(\pi\mathrm{x}\right)\right)\:=\frac{\mathrm{x}+\mathrm{2}}{\left(\mathrm{x}+\mathrm{2}\right)^{\mathrm{2}} +\pi^{\mathrm{2}} } \\ $$
