Question Number 97539 by bobhans last updated on 08/Jun/20
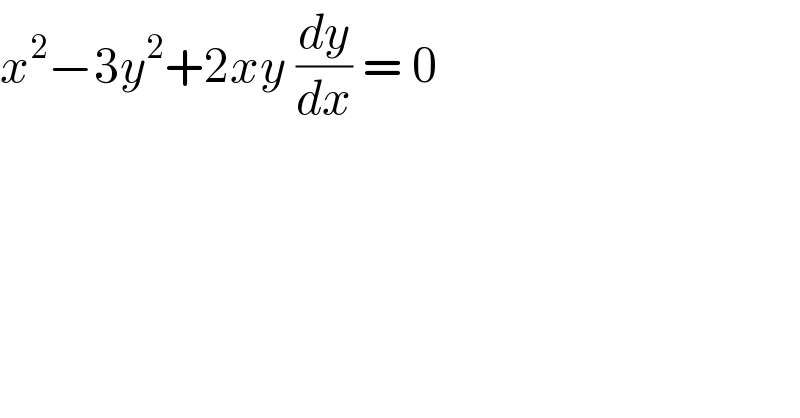
$${x}^{\mathrm{2}} −\mathrm{3}{y}^{\mathrm{2}} +\mathrm{2}{xy}\:\frac{{dy}}{{dx}}\:=\:\mathrm{0} \\ $$
Answered by bemath last updated on 08/Jun/20

Commented by bobhans last updated on 08/Jun/20

$$\mathrm{coolll} \\ $$
Answered by smridha last updated on 08/Jun/20
![(x^2 −3y^2 )dx+2xydy=0....(i) (∂/∂y)(x^2 −3y^2 )=−6y≠(∂/∂x)(2xy)=2y so this is not exact differential (1/(2xy))[−6y−2y]=−(4/x) I.F=e^(∫−(4/x)dx) =(1/x^4 ) multi:by (1/x^4 ) bothsides of eq^n (i) ((1/x^2 )−((3y^2 )/x^4 ))dx+((2y)/x^3 )dy=0 ∫_((keeping y as constant)) ((1/x^2 )−((3y^2 )/x^4 ))dx =−(1/x)+(y^2 /x^3 ) ∫_((terms which are not containing x) ) (0)dy=0 so eq^n : −(1/x)+(y^2 /x^3 )=c](https://www.tinkutara.com/question/Q97611.png)
$$\left(\boldsymbol{{x}}^{\mathrm{2}} −\mathrm{3}\boldsymbol{{y}}^{\mathrm{2}} \right)\boldsymbol{{dx}}+\mathrm{2}\boldsymbol{{xydy}}=\mathrm{0}….\left(\boldsymbol{{i}}\right) \\ $$$$\frac{\partial}{\partial\boldsymbol{{y}}}\left(\boldsymbol{{x}}^{\mathrm{2}} −\mathrm{3}\boldsymbol{{y}}^{\mathrm{2}} \right)=−\mathrm{6}\boldsymbol{{y}}\neq\frac{\partial}{\partial\boldsymbol{{x}}}\left(\mathrm{2}\boldsymbol{{xy}}\right)=\mathrm{2}\boldsymbol{{y}} \\ $$$$\boldsymbol{{so}}\:\boldsymbol{{this}}\:\boldsymbol{{is}}\:\boldsymbol{{not}}\:\boldsymbol{{exact}}\:\boldsymbol{{differential}} \\ $$$$\frac{\mathrm{1}}{\mathrm{2}\boldsymbol{{xy}}}\left[−\mathrm{6}\boldsymbol{{y}}−\mathrm{2}\boldsymbol{{y}}\right]=−\frac{\mathrm{4}}{\boldsymbol{{x}}}\:\boldsymbol{{I}}.\boldsymbol{{F}}=\boldsymbol{{e}}^{\int−\frac{\mathrm{4}}{\boldsymbol{{x}}}\boldsymbol{{dx}}} =\frac{\mathrm{1}}{\boldsymbol{{x}}^{\mathrm{4}} } \\ $$$$\boldsymbol{{multi}}:\boldsymbol{{by}}\:\frac{\mathrm{1}}{{x}^{\mathrm{4}} }\:\boldsymbol{{bothsides}}\:\boldsymbol{{of}}\:\boldsymbol{{eq}}^{\boldsymbol{{n}}} \left(\boldsymbol{{i}}\right) \\ $$$$\left(\frac{\mathrm{1}}{\boldsymbol{{x}}^{\mathrm{2}} }−\frac{\mathrm{3}\boldsymbol{{y}}^{\mathrm{2}} }{\boldsymbol{{x}}^{\mathrm{4}} }\right)\boldsymbol{{dx}}+\frac{\mathrm{2}\boldsymbol{{y}}}{\boldsymbol{{x}}^{\mathrm{3}} }\boldsymbol{{dy}}=\mathrm{0} \\ $$$$\int_{\left(\boldsymbol{{keeping}}\:\boldsymbol{{y}}\:\boldsymbol{{as}}\:\boldsymbol{{constant}}\right)} \left(\frac{\mathrm{1}}{\boldsymbol{{x}}^{\mathrm{2}} }−\frac{\mathrm{3}\boldsymbol{{y}}^{\mathrm{2}} }{\boldsymbol{{x}}^{\mathrm{4}} }\right)\boldsymbol{{dx}} \\ $$$$=−\frac{\mathrm{1}}{\boldsymbol{{x}}}+\frac{\boldsymbol{{y}}^{\mathrm{2}} }{\boldsymbol{{x}}^{\mathrm{3}} } \\ $$$$\int_{\left({terms}\:\boldsymbol{{which}}\:\boldsymbol{{are}}\:\boldsymbol{{not}}\:\boldsymbol{{contain}}{ing}\:\boldsymbol{{x}}\right)\:} \left(\mathrm{0}\right)\boldsymbol{{dy}}=\mathrm{0} \\ $$$$\boldsymbol{{so}}\:\boldsymbol{{eq}}^{\boldsymbol{{n}}} :\:\:−\frac{\mathrm{1}}{\boldsymbol{{x}}}+\frac{\boldsymbol{{y}}^{\mathrm{2}} }{\boldsymbol{{x}}^{\mathrm{3}} }=\boldsymbol{{c}} \\ $$
