Question Number 32026 by abdo imad last updated on 18/Mar/18
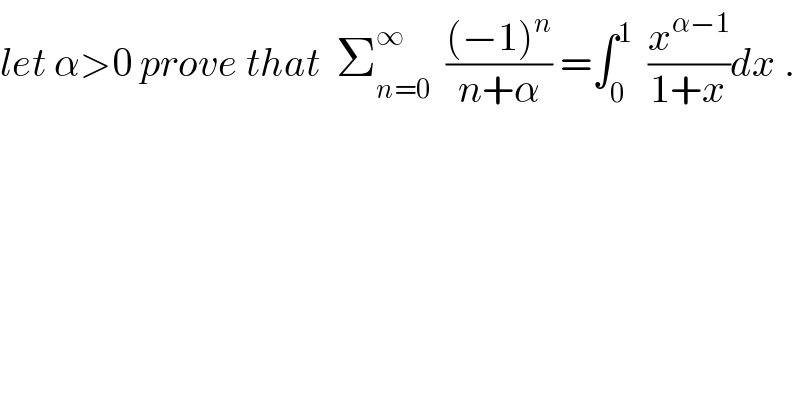
$${let}\:\alpha>\mathrm{0}\:{prove}\:{that}\:\:\sum_{{n}=\mathrm{0}} ^{\infty} \:\:\frac{\left(−\mathrm{1}\right)^{{n}} }{{n}+\alpha}\:=\int_{\mathrm{0}} ^{\mathrm{1}} \:\:\frac{{x}^{\alpha−\mathrm{1}} }{\mathrm{1}+{x}}{dx}\:. \\ $$
Commented by abdo imad last updated on 22/Mar/18
![∫_0 ^1 (x^(α−1) /(1+x))dx = ∫_0 ^1 (Σ_(n=0) ^∞ (−1)^n x^n )x^(α−1) dx = Σ_(n=0) ^∞ (−1)^n ∫_0 ^1 x^(n+α−1) dx =Σ_(n=0) ^∞ (−1)^n [ (1/(n+α)) x^(n+α) ]_0 ^1 =Σ_(n=0) ^∞ (((−1)^n )/(n+α)) .](https://www.tinkutara.com/question/Q32231.png)
$$\int_{\mathrm{0}} ^{\mathrm{1}} \:\:\frac{{x}^{\alpha−\mathrm{1}} }{\mathrm{1}+{x}}{dx}\:=\:\int_{\mathrm{0}} ^{\mathrm{1}} \left(\sum_{{n}=\mathrm{0}} ^{\infty} \left(−\mathrm{1}\right)^{{n}} {x}^{{n}} \right){x}^{\alpha−\mathrm{1}} {dx} \\ $$$$=\:\sum_{{n}=\mathrm{0}} ^{\infty} \:\left(−\mathrm{1}\right)^{{n}} \:\int_{\mathrm{0}} ^{\mathrm{1}} \:{x}^{{n}+\alpha−\mathrm{1}} {dx} \\ $$$$=\sum_{{n}=\mathrm{0}} ^{\infty} \:\left(−\mathrm{1}\right)^{{n}} \:\left[\:\frac{\mathrm{1}}{{n}+\alpha}\:{x}^{{n}+\alpha} \right]_{\mathrm{0}} ^{\mathrm{1}} \:=\sum_{{n}=\mathrm{0}} ^{\infty} \:\:\frac{\left(−\mathrm{1}\right)^{{n}} }{{n}+\alpha}\:. \\ $$
