Question Number 164345 by mr W last updated on 16/Jan/22

Commented by mr W last updated on 18/Jan/22
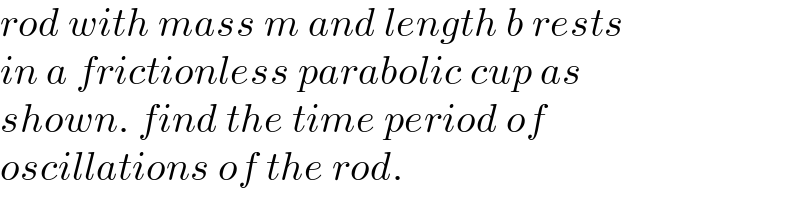
$${rod}\:{with}\:{mass}\:{m}\:{and}\:{length}\:{b}\:{rests} \\ $$$${in}\:{a}\:{frictionless}\:{parabolic}\:{cup}\:{as} \\ $$$${shown}.\:{find}\:{the}\:{time}\:{period}\:{of} \\ $$$${oscillations}\:{of}\:{the}\:{rod}. \\ $$
Answered by ajfour last updated on 16/Jan/22
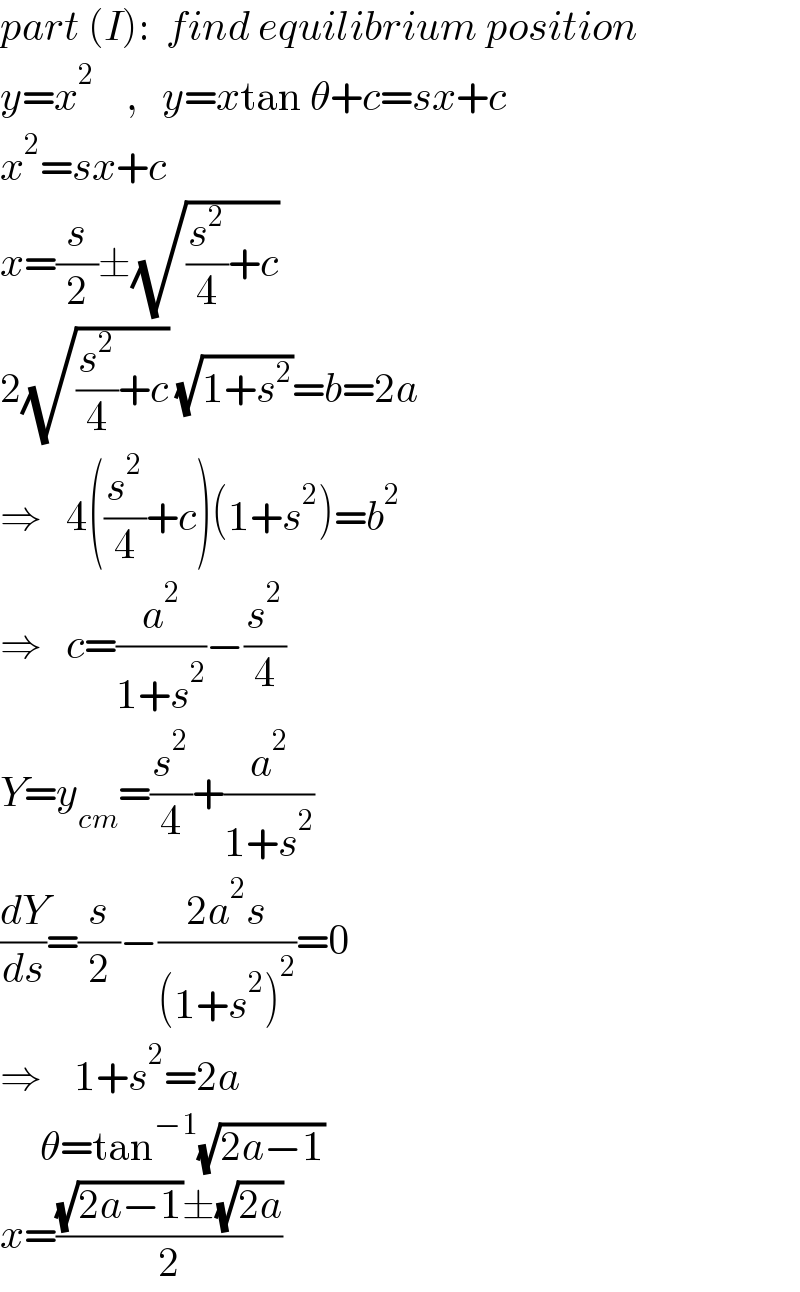
$${part}\:\left({I}\right):\:\:{find}\:{equilibrium}\:{position} \\ $$$${y}={x}^{\mathrm{2}} \:\:\:\:,\:\:\:{y}={x}\mathrm{tan}\:\theta+{c}={sx}+{c} \\ $$$${x}^{\mathrm{2}} ={sx}+{c} \\ $$$${x}=\frac{{s}}{\mathrm{2}}\pm\sqrt{\frac{{s}^{\mathrm{2}} }{\mathrm{4}}+{c}} \\ $$$$\mathrm{2}\sqrt{\frac{{s}^{\mathrm{2}} }{\mathrm{4}}+{c}}\:\sqrt{\mathrm{1}+{s}^{\mathrm{2}} }={b}=\mathrm{2}{a} \\ $$$$\Rightarrow\:\:\:\mathrm{4}\left(\frac{{s}^{\mathrm{2}} }{\mathrm{4}}+{c}\right)\left(\mathrm{1}+{s}^{\mathrm{2}} \right)={b}^{\mathrm{2}} \\ $$$$\Rightarrow\:\:\:{c}=\frac{{a}^{\mathrm{2}} }{\mathrm{1}+{s}^{\mathrm{2}} }−\frac{{s}^{\mathrm{2}} }{\mathrm{4}} \\ $$$${Y}={y}_{{cm}} =\frac{{s}^{\mathrm{2}} }{\mathrm{4}}+\frac{{a}^{\mathrm{2}} }{\mathrm{1}+{s}^{\mathrm{2}} } \\ $$$$\frac{{dY}}{{ds}}=\frac{{s}}{\mathrm{2}}−\frac{\mathrm{2}{a}^{\mathrm{2}} {s}}{\left(\mathrm{1}+{s}^{\mathrm{2}} \right)^{\mathrm{2}} }=\mathrm{0} \\ $$$$\Rightarrow\:\:\:\:\mathrm{1}+{s}^{\mathrm{2}} =\mathrm{2}{a} \\ $$$$\:\:\:\:\:\theta=\mathrm{tan}^{−\mathrm{1}} \sqrt{\mathrm{2}{a}−\mathrm{1}} \\ $$$${x}=\frac{\sqrt{\mathrm{2}{a}−\mathrm{1}}\pm\sqrt{\mathrm{2}{a}}}{\mathrm{2}} \\ $$
Commented by mr W last updated on 17/Jan/22
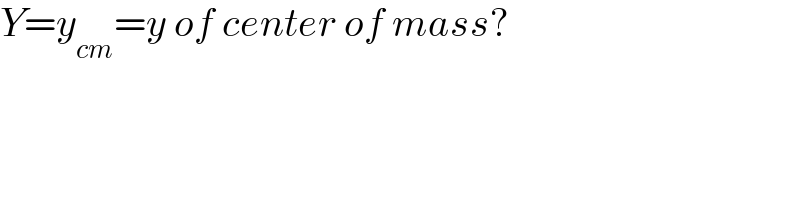
$${Y}={y}_{{cm}} ={y}\:{of}\:{center}\:{of}\:{mass}? \\ $$
Commented by ajfour last updated on 18/Jan/22
yes sir.
Commented by mr W last updated on 18/Jan/22
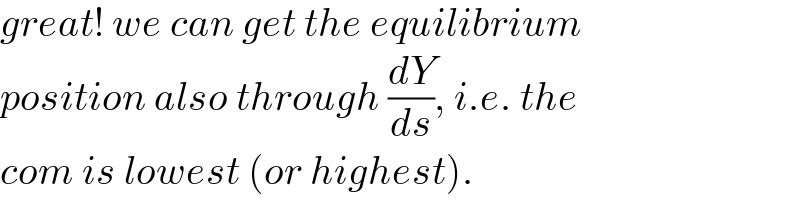
$${great}!\:{we}\:{can}\:{get}\:{the}\:{equilibrium} \\ $$$${position}\:{also}\:{through}\:\frac{{dY}}{{ds}},\:{i}.{e}.\:{the} \\ $$$${com}\:{is}\:{lowest}\:\left({or}\:{highest}\right). \\ $$
Answered by mr W last updated on 17/Jan/22

Commented by mr W last updated on 18/Jan/22
![see also Q164073 parabola y=(x^2 /a) with a=1 here length of rod is b. C=center of mass say the end points of the rod are A(−p, (p^2 /a)), B(q, (q^2 /a)) tan φ=−(dy/dx)∣_(x=−p) =((2p)/a) tan ϕ=(dy/dx)∣_(x=q) =((2q)/a) tan γ=(((q^2 /a)−(p^2 /a))/(q+p))=((q^2 −p^2 )/(a(q+p)))=((q−p)/a) α=(π/2)−φ−γ β=(π/2)−ϕ+γ ((SC)/(AC))=((sin α)/(sin φ))=((sin ((π/2)−φ−γ))/(sin φ))=((cos (φ+γ))/(sin φ)) ((SC)/(CB))=((sin β)/(sin ϕ))=((sin ((π/2)−ϕ+γ))/(sin ϕ))=((cos (ϕ−γ))/(sin ϕ)) since AC=CB=(b/2), ((cos (φ+γ))/(sin φ))=((cos (ϕ−γ))/(sin ϕ)) ((cos φ cos γ−sin φ sin γ)/(sin φ))=((cos ϕ cos γ+sin ϕ sin γ)/(sin ϕ)) ((cos γ)/(tan φ))−sin γ=((cos γ)/(tan ϕ))+sin γ (1/(tan φ))−(1/(tan ϕ))=2 tan γ (a/(2p))−(a/(2q))=((2(q−p))/a) ((q−p)/(pq))=((4(q−p))/a^2 ) ⇒q−p=0 ⇒p=q ⇒horizontal position or ⇒(1/(pq))=(4/a^2 ) ⇒pq=(a^2 /4) ⇒inclined position we consider the inclined position of rod, which is generally the only stable equilibrium position. (q+p)^2 +((q^2 /a)−(p^2 /a))^2 =b^2 (q+p)^2 [1+(((q−p)^2 )/a^2 )]=b^2 (q+p)^2 [1+(((q+p)^2 −4pq)/a^2 )]=b^2 (q+p)^2 [1+(((q+p)^2 −a^2 )/a^2 )]=b^2 (q+p)^4 =a^2 b^2 ⇒p+q=(√(ab)) p and q are roots of z^2 −(√(ab))z+(a^2 /4)=0 ⇒p=(((√(ab))−(√(a(b−a))))/2) ⇒q=(((√(ab))+(√(a(b−a))))/2) tan (ϕ+φ)=((((2p)/a)+((2q)/a))/(1−((2p)/a)×((2q)/a)))=((2a(p+q))/(a^2 −4pq))=((2a(p+q))/(a^2 −a^2 )) ⇒ϕ+φ=90° ⇒SA⊥SB ⇒SC=((AB)/2)=(b/2) h=SC×θ=((bθ)/2) I_S =((mb^2 )/(12))+m((b/2))^2 =((mb^2 )/3) I_S (d^2 θ/dt^2 )=−mgh ((mb^2 )/3) (d^2 θ/dt^2 )=−mg((bθ)/2) (d^2 θ/dt^2 )+((3g)/(2b))θ=0 ω=(√((3g)/(2b))) ⇒T=((2π)/ω)=2π(√((2b)/(3g)))](https://www.tinkutara.com/question/Q164476.png)
$${see}\:{also}\:{Q}\mathrm{164073} \\ $$$${parabola}\:{y}=\frac{{x}^{\mathrm{2}} }{{a}}\:{with}\:{a}=\mathrm{1}\:{here} \\ $$$${length}\:{of}\:{rod}\:{is}\:{b}. \\ $$$${C}={center}\:{of}\:{mass} \\ $$$${say}\:{the}\:{end}\:{points}\:{of}\:{the}\:{rod}\:{are} \\ $$$${A}\left(−{p},\:\frac{{p}^{\mathrm{2}} }{{a}}\right),\:{B}\left({q},\:\frac{{q}^{\mathrm{2}} }{{a}}\right) \\ $$$$\mathrm{tan}\:\phi=−\frac{{dy}}{{dx}}\mid_{{x}=−{p}} =\frac{\mathrm{2}{p}}{{a}} \\ $$$$\mathrm{tan}\:\varphi=\frac{{dy}}{{dx}}\mid_{{x}={q}} =\frac{\mathrm{2}{q}}{{a}} \\ $$$$\mathrm{tan}\:\gamma=\frac{\frac{{q}^{\mathrm{2}} }{{a}}−\frac{{p}^{\mathrm{2}} }{{a}}}{{q}+{p}}=\frac{{q}^{\mathrm{2}} −{p}^{\mathrm{2}} }{{a}\left({q}+{p}\right)}=\frac{{q}−{p}}{{a}} \\ $$$$\alpha=\frac{\pi}{\mathrm{2}}−\phi−\gamma \\ $$$$\beta=\frac{\pi}{\mathrm{2}}−\varphi+\gamma \\ $$$$\frac{{SC}}{{AC}}=\frac{\mathrm{sin}\:\alpha}{\mathrm{sin}\:\phi}=\frac{\mathrm{sin}\:\left(\frac{\pi}{\mathrm{2}}−\phi−\gamma\right)}{\mathrm{sin}\:\phi}=\frac{\mathrm{cos}\:\left(\phi+\gamma\right)}{\mathrm{sin}\:\phi} \\ $$$$\frac{{SC}}{{CB}}=\frac{\mathrm{sin}\:\beta}{\mathrm{sin}\:\varphi}=\frac{\mathrm{sin}\:\left(\frac{\pi}{\mathrm{2}}−\varphi+\gamma\right)}{\mathrm{sin}\:\varphi}=\frac{\mathrm{cos}\:\left(\varphi−\gamma\right)}{\mathrm{sin}\:\varphi} \\ $$$${since}\:{AC}={CB}=\frac{{b}}{\mathrm{2}}, \\ $$$$\frac{\mathrm{cos}\:\left(\phi+\gamma\right)}{\mathrm{sin}\:\phi}=\frac{\mathrm{cos}\:\left(\varphi−\gamma\right)}{\mathrm{sin}\:\varphi} \\ $$$$\frac{\mathrm{cos}\:\phi\:\mathrm{cos}\:\gamma−\mathrm{sin}\:\phi\:\mathrm{sin}\:\gamma}{\mathrm{sin}\:\phi}=\frac{\mathrm{cos}\:\varphi\:\mathrm{cos}\:\gamma+\mathrm{sin}\:\varphi\:\mathrm{sin}\:\gamma}{\mathrm{sin}\:\varphi} \\ $$$$\frac{\mathrm{cos}\:\gamma}{\mathrm{tan}\:\phi}−\mathrm{sin}\:\gamma=\frac{\mathrm{cos}\:\gamma}{\mathrm{tan}\:\varphi}+\mathrm{sin}\:\gamma \\ $$$$\frac{\mathrm{1}}{\mathrm{tan}\:\phi}−\frac{\mathrm{1}}{\mathrm{tan}\:\varphi}=\mathrm{2}\:\mathrm{tan}\:\gamma \\ $$$$\frac{{a}}{\mathrm{2}{p}}−\frac{{a}}{\mathrm{2}{q}}=\frac{\mathrm{2}\left({q}−{p}\right)}{{a}} \\ $$$$\frac{{q}−{p}}{{pq}}=\frac{\mathrm{4}\left({q}−{p}\right)}{{a}^{\mathrm{2}} } \\ $$$$\Rightarrow{q}−{p}=\mathrm{0}\:\Rightarrow{p}={q}\:\Rightarrow{horizontal}\:{position} \\ $$$${or} \\ $$$$\Rightarrow\frac{\mathrm{1}}{{pq}}=\frac{\mathrm{4}}{{a}^{\mathrm{2}} } \\ $$$$\Rightarrow{pq}=\frac{{a}^{\mathrm{2}} }{\mathrm{4}}\:\Rightarrow{inclined}\:{position} \\ $$$${we}\:{consider}\:{the}\:{inclined}\:{position} \\ $$$${of}\:{rod},\:{which}\:{is}\:{generally}\:{the}\:{only}\: \\ $$$${stable}\:{equilibrium}\:{position}. \\ $$$$\left({q}+{p}\right)^{\mathrm{2}} +\left(\frac{{q}^{\mathrm{2}} }{{a}}−\frac{{p}^{\mathrm{2}} }{{a}}\right)^{\mathrm{2}} ={b}^{\mathrm{2}} \\ $$$$\left({q}+{p}\right)^{\mathrm{2}} \left[\mathrm{1}+\frac{\left({q}−{p}\right)^{\mathrm{2}} }{{a}^{\mathrm{2}} }\right]={b}^{\mathrm{2}} \\ $$$$\left({q}+{p}\right)^{\mathrm{2}} \left[\mathrm{1}+\frac{\left({q}+{p}\right)^{\mathrm{2}} −\mathrm{4}{pq}}{{a}^{\mathrm{2}} }\right]={b}^{\mathrm{2}} \\ $$$$\left({q}+{p}\right)^{\mathrm{2}} \left[\mathrm{1}+\frac{\left({q}+{p}\right)^{\mathrm{2}} −{a}^{\mathrm{2}} }{{a}^{\mathrm{2}} }\right]={b}^{\mathrm{2}} \\ $$$$\left({q}+{p}\right)^{\mathrm{4}} ={a}^{\mathrm{2}} {b}^{\mathrm{2}} \\ $$$$\Rightarrow{p}+{q}=\sqrt{{ab}} \\ $$$${p}\:{and}\:{q}\:{are}\:{roots}\:{of} \\ $$$${z}^{\mathrm{2}} −\sqrt{{ab}}{z}+\frac{{a}^{\mathrm{2}} }{\mathrm{4}}=\mathrm{0} \\ $$$$\Rightarrow{p}=\frac{\sqrt{{ab}}−\sqrt{{a}\left({b}−{a}\right)}}{\mathrm{2}} \\ $$$$\Rightarrow{q}=\frac{\sqrt{{ab}}+\sqrt{{a}\left({b}−{a}\right)}}{\mathrm{2}} \\ $$$$\mathrm{tan}\:\left(\varphi+\phi\right)=\frac{\frac{\mathrm{2}{p}}{{a}}+\frac{\mathrm{2}{q}}{{a}}}{\mathrm{1}−\frac{\mathrm{2}{p}}{{a}}×\frac{\mathrm{2}{q}}{{a}}}=\frac{\mathrm{2}{a}\left({p}+{q}\right)}{{a}^{\mathrm{2}} −\mathrm{4}{pq}}=\frac{\mathrm{2}{a}\left({p}+{q}\right)}{{a}^{\mathrm{2}} −{a}^{\mathrm{2}} } \\ $$$$\Rightarrow\varphi+\phi=\mathrm{90}°\:\Rightarrow{SA}\bot{SB} \\ $$$$\Rightarrow{SC}=\frac{{AB}}{\mathrm{2}}=\frac{{b}}{\mathrm{2}} \\ $$$${h}={SC}×\theta=\frac{{b}\theta}{\mathrm{2}} \\ $$$${I}_{{S}} =\frac{{mb}^{\mathrm{2}} }{\mathrm{12}}+{m}\left(\frac{{b}}{\mathrm{2}}\right)^{\mathrm{2}} =\frac{{mb}^{\mathrm{2}} }{\mathrm{3}} \\ $$$${I}_{{S}} \:\frac{{d}^{\mathrm{2}} \theta}{{dt}^{\mathrm{2}} }=−{mgh} \\ $$$$\frac{{mb}^{\mathrm{2}} }{\mathrm{3}}\:\frac{{d}^{\mathrm{2}} \theta}{{dt}^{\mathrm{2}} }=−{mg}\frac{{b}\theta}{\mathrm{2}} \\ $$$$\:\frac{{d}^{\mathrm{2}} \theta}{{dt}^{\mathrm{2}} }+\frac{\mathrm{3}{g}}{\mathrm{2}{b}}\theta=\mathrm{0} \\ $$$$\omega=\sqrt{\frac{\mathrm{3}{g}}{\mathrm{2}{b}}} \\ $$$$\Rightarrow{T}=\frac{\mathrm{2}\pi}{\omega}=\mathrm{2}\pi\sqrt{\frac{\mathrm{2}{b}}{\mathrm{3}{g}}} \\ $$
Commented by mr W last updated on 18/Jan/22
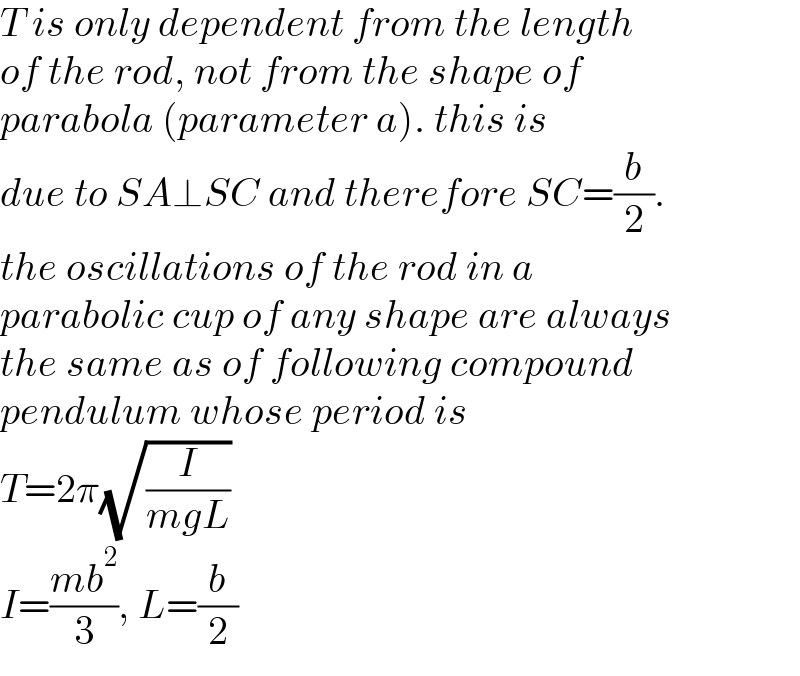
$${T}\:{is}\:{only}\:{dependent}\:{from}\:{the}\:{length} \\ $$$${of}\:{the}\:{rod},\:{not}\:{from}\:{the}\:{shape}\:{of}\: \\ $$$${parabola}\:\left({parameter}\:{a}\right).\:{this}\:{is} \\ $$$${due}\:{to}\:{SA}\bot{SC}\:{and}\:{therefore}\:{SC}=\frac{{b}}{\mathrm{2}}.\: \\ $$$${the}\:{oscillations}\:{of}\:{the}\:{rod}\:{in}\:{a}\: \\ $$$${parabolic}\:{cup}\:{of}\:{any}\:{shape}\:{are}\:{always} \\ $$$${the}\:{same}\:{as}\:{of}\:{following}\:{compound} \\ $$$${pendulum}\:{whose}\:{period}\:{is} \\ $$$${T}=\mathrm{2}\pi\sqrt{\frac{{I}}{{mgL}}} \\ $$$${I}=\frac{{mb}^{\mathrm{2}} }{\mathrm{3}},\:{L}=\frac{{b}}{\mathrm{2}} \\ $$
Commented by mr W last updated on 18/Jan/22

Commented by Tawa11 last updated on 18/Jan/22

$$\mathrm{Great}\:\mathrm{sirs} \\ $$
