Question Number 98821 by bramlex last updated on 16/Jun/20
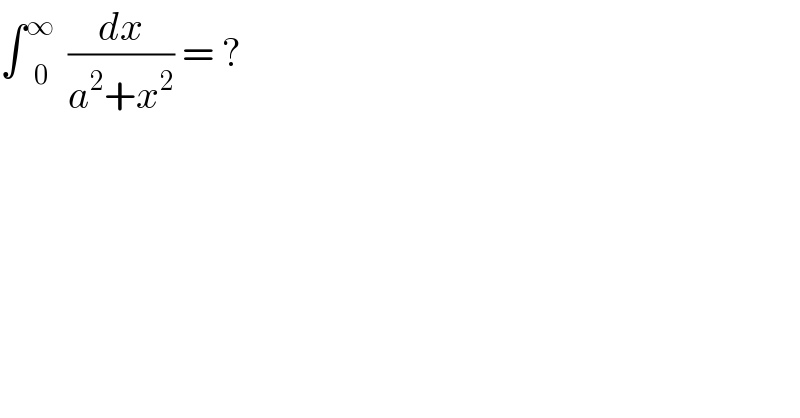
$$\int\overset{\infty} {\:}_{\mathrm{0}} \frac{{dx}}{{a}^{\mathrm{2}} +{x}^{\mathrm{2}} }\:=\:? \\ $$
Answered by Ar Brandon last updated on 16/Jun/20
![I=(1/a)[arctan((x/a))]_0 ^∞ =(1/a)[(π/2)−0] { (),() :}since tan[(π/2)]=+∞} ⇒∫ _0 ^∞ (dx/(a^2 +x^2 )) =(π/(2a))](https://www.tinkutara.com/question/Q98822.png)
$$\left.\mathcal{I}=\frac{\mathrm{1}}{\mathrm{a}}\left[\mathrm{arctan}\left(\frac{\mathrm{x}}{\mathrm{a}}\right)\right]_{\mathrm{0}} ^{\infty} =\frac{\mathrm{1}}{\mathrm{a}}\left[\frac{\pi}{\mathrm{2}}−\mathrm{0}\right]\:\begin{cases}{}\\{}\end{cases}\mathrm{since}\:\mathrm{tan}\left[\frac{\pi}{\mathrm{2}}\right]=+\infty\right\} \\ $$$$\Rightarrow\int\overset{\infty} {\:}_{\mathrm{0}} \frac{{dx}}{{a}^{\mathrm{2}} +{x}^{\mathrm{2}} }\:=\frac{\pi}{\mathrm{2a}} \\ $$
Commented by bramlex last updated on 16/Jun/20

$${thanks} \\ $$
