Question Number 33351 by caravan msup abdo. last updated on 14/Apr/18
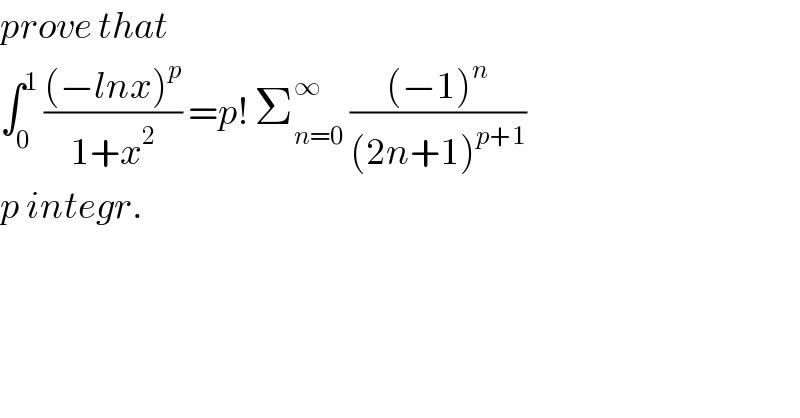
$${prove}\:{that} \\ $$$$\int_{\mathrm{0}} ^{\mathrm{1}} \:\frac{\left(−{lnx}\right)^{{p}} }{\mathrm{1}+{x}^{\mathrm{2}} }\:={p}!\:\sum_{{n}=\mathrm{0}} ^{\infty} \:\frac{\left(−\mathrm{1}\right)^{{n}} }{\left(\mathrm{2}{n}+\mathrm{1}\right)^{{p}+\mathrm{1}} } \\ $$$${p}\:{integr}. \\ $$
Commented by math khazana by abdo last updated on 19/Apr/18
![let put A_p = ∫_0 ^1 (((−lnx)^p )/(1+x^2 ))dx A_p = (−1)^p ∫_0 ^1 (((lnx)^p )/(1+x^2 ))dx =(−1)^p ∫_0 ^1 ( Σ_(n=0) ^∞ (−1)^n x^(2n) )(lnx)^p dx = Σ_(n=0) ^∞ (−1)^(n+p) ∫_0 ^1 x^(2n) (lnx)^p dx let find I_(n,p) = ∫_0 ^1 x^n (lnx)^p dx by parts I_(n,p) = [(1/(n+1)) x^(n+1) (lnx)^p ]_0 ^1 − ∫_0 ^1 (1/(n+1))x^(n+1) (p/x) (lnx)^(p−1) =−(p/(n+1)) ∫_0 ^1 x^n (lnx)^(p−1) dx =((−p)/(n+1)) I_(n,p−1) ⇒ I_(n,p) = (((−p)(−(p−1)))/((n+1)^2 )) I_(n,p−2) =....= (((−1)^p p!)/((n+1)^p )) I_(n,0) I_(n,0) = ∫_0 ^1 x^n dx = (1/(n+1)) ⇒ I_(n,p) = (((−1)^p p!)/((n+1)^(p+1) )) ⇒ ∫_0 ^1 x^(2n) (lnx)^p dx = (((−1)^p p!)/((2n+1)^(p+1) )) and A_p =Σ_(n=0) ^∞ (−1)^(n+p) (((−1)^p p!)/((2n+1)^(p+1) )) =p! Σ_(n=0) ^∞ (((−1)^n )/((2n+1)^(p+1) )) .](https://www.tinkutara.com/question/Q33562.png)
$${let}\:{put}\:{A}_{{p}} =\:\int_{\mathrm{0}} ^{\mathrm{1}} \:\:\:\frac{\left(−{lnx}\right)^{{p}} }{\mathrm{1}+{x}^{\mathrm{2}} }{dx} \\ $$$${A}_{{p}} =\:\left(−\mathrm{1}\right)^{{p}} \:\:\int_{\mathrm{0}} ^{\mathrm{1}} \:\:\:\frac{\left({lnx}\right)^{{p}} }{\mathrm{1}+{x}^{\mathrm{2}} }{dx} \\ $$$$=\left(−\mathrm{1}\right)^{{p}} \:\int_{\mathrm{0}} ^{\mathrm{1}} \left(\:\sum_{{n}=\mathrm{0}} ^{\infty} \left(−\mathrm{1}\right)^{{n}} \:{x}^{\mathrm{2}{n}} \right)\left({lnx}\right)^{{p}} {dx} \\ $$$$=\:\sum_{{n}=\mathrm{0}} ^{\infty} \:\left(−\mathrm{1}\right)^{{n}+{p}} \:\:\int_{\mathrm{0}} ^{\mathrm{1}} \:\:\:{x}^{\mathrm{2}{n}} \:\left({lnx}\right)^{{p}} \:{dx}\:\:{let}\:{find} \\ $$$${I}_{{n},{p}} =\:\int_{\mathrm{0}} ^{\mathrm{1}} \:\:{x}^{{n}} \:\left({lnx}\right)^{{p}} {dx}\:\:\:{by}\:{parts} \\ $$$${I}_{{n},{p}} =\:\left[\frac{\mathrm{1}}{{n}+\mathrm{1}}\:{x}^{{n}+\mathrm{1}} \left({lnx}\right)^{{p}} \:\right]_{\mathrm{0}} ^{\mathrm{1}} \:\:−\:\int_{\mathrm{0}} ^{\mathrm{1}} \:\:\:\frac{\mathrm{1}}{{n}+\mathrm{1}}{x}^{{n}+\mathrm{1}} \:\:\frac{{p}}{{x}}\:\left({lnx}\right)^{{p}−\mathrm{1}} \\ $$$$=−\frac{{p}}{{n}+\mathrm{1}}\:\int_{\mathrm{0}} ^{\mathrm{1}} \:\:{x}^{{n}} \:\left({lnx}\right)^{{p}−\mathrm{1}} \:{dx}\:=\frac{−{p}}{{n}+\mathrm{1}}\:{I}_{{n},{p}−\mathrm{1}} \:\Rightarrow \\ $$$${I}_{{n},{p}} \:\:=\:\frac{\left(−{p}\right)\left(−\left({p}−\mathrm{1}\right)\right)}{\left({n}+\mathrm{1}\right)^{\mathrm{2}} }\:{I}_{{n},{p}−\mathrm{2}} \:=….=\:\frac{\left(−\mathrm{1}\right)^{{p}} {p}!}{\left({n}+\mathrm{1}\right)^{{p}} }\:\:{I}_{{n},\mathrm{0}} \\ $$$${I}_{{n},\mathrm{0}} =\:\int_{\mathrm{0}} ^{\mathrm{1}} \:{x}^{{n}} \:{dx}\:=\:\frac{\mathrm{1}}{{n}+\mathrm{1}}\:\Rightarrow\:{I}_{{n},{p}} \:=\:\frac{\left(−\mathrm{1}\right)^{{p}} \:{p}!}{\left({n}+\mathrm{1}\right)^{{p}+\mathrm{1}} }\:\:\Rightarrow \\ $$$$\int_{\mathrm{0}} ^{\mathrm{1}} \:{x}^{\mathrm{2}{n}} \left({lnx}\right)^{{p}} {dx}\:=\:\frac{\left(−\mathrm{1}\right)^{{p}} \:{p}!}{\left(\mathrm{2}{n}+\mathrm{1}\right)^{{p}+\mathrm{1}} }\:\:{and} \\ $$$${A}_{{p}} \:=\sum_{{n}=\mathrm{0}} ^{\infty} \:\left(−\mathrm{1}\right)^{{n}+{p}} \:\:\frac{\left(−\mathrm{1}\right)^{{p}} \:{p}!}{\left(\mathrm{2}{n}+\mathrm{1}\right)^{{p}+\mathrm{1}} } \\ $$$$={p}!\:\sum_{{n}=\mathrm{0}} ^{\infty} \:\:\:\frac{\left(−\mathrm{1}\right)^{\boldsymbol{{n}}} }{\left(\mathrm{2}\boldsymbol{{n}}+\mathrm{1}\right)^{\boldsymbol{{p}}+\mathrm{1}} }\:. \\ $$$$ \\ $$
