Question Number 99193 by bemath last updated on 19/Jun/20

Commented by I want to learn more last updated on 19/Jun/20
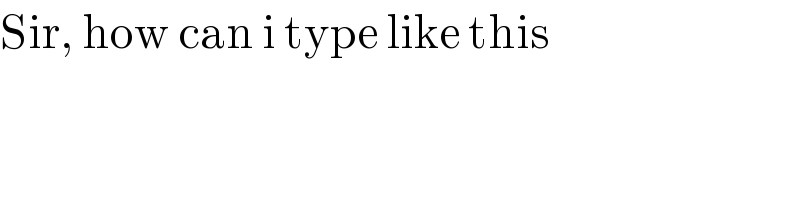
$$\mathrm{Sir},\:\mathrm{how}\:\mathrm{can}\:\mathrm{i}\:\mathrm{type}\:\mathrm{like}\:\mathrm{this} \\ $$
Commented by Ar Brandon last updated on 19/Jun/20
You can do that on the home page.
Commented by bemath last updated on 19/Jun/20
Enter the editor menu, select font and color and then set the background color
Commented by I want to learn more last updated on 19/Jun/20

$$\mathrm{Thanks}\:\mathrm{sir} \\ $$
Answered by Ar Brandon last updated on 19/Jun/20
![L=lim_(n→∞) Σ_(k=1) ^n ((k/n^4 ))^(1/3) =lim_(n→∞) (1/n)Σ_(k=1) ^n ((k/n))^(1/3) ⇒L=∫_0 ^1 (x)^(1/3) dx=[(3/4)x^(4/3) ]_0 ^1 =(3/4)](https://www.tinkutara.com/question/Q99203.png)
$$\mathrm{L}=\underset{\mathrm{n}\rightarrow\infty} {\mathrm{lim}}\underset{\mathrm{k}=\mathrm{1}} {\overset{\mathrm{n}} {\sum}}\sqrt[{\mathrm{3}}]{\frac{\mathrm{k}}{\mathrm{n}^{\mathrm{4}} }}=\underset{\mathrm{n}\rightarrow\infty} {\mathrm{lim}}\frac{\mathrm{1}}{\mathrm{n}}\underset{\mathrm{k}=\mathrm{1}} {\overset{\mathrm{n}} {\sum}}\sqrt[{\mathrm{3}}]{\frac{\mathrm{k}}{\mathrm{n}}} \\ $$$$\Rightarrow\mathrm{L}=\int_{\mathrm{0}} ^{\mathrm{1}} \sqrt[{\mathrm{3}}]{\mathrm{x}}\mathrm{dx}=\left[\frac{\mathrm{3}}{\mathrm{4}}\mathrm{x}^{\frac{\mathrm{4}}{\mathrm{3}}} \right]_{\mathrm{0}} ^{\mathrm{1}} =\frac{\mathrm{3}}{\mathrm{4}} \\ $$
Commented by bemath last updated on 19/Jun/20
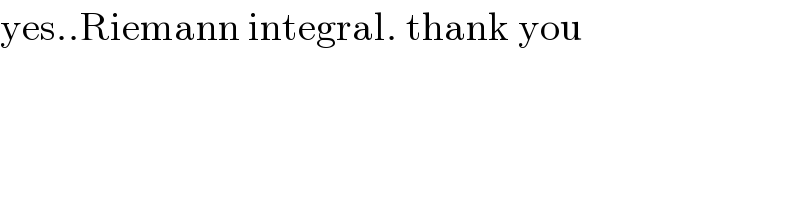
$$\mathrm{yes}..\mathrm{Riemann}\:\mathrm{integral}.\:\mathrm{thank}\:\mathrm{you} \\ $$
Commented by Ar Brandon last updated on 19/Jun/20
Cool��
