Question Number 33677 by math khazana by abdo last updated on 21/Apr/18
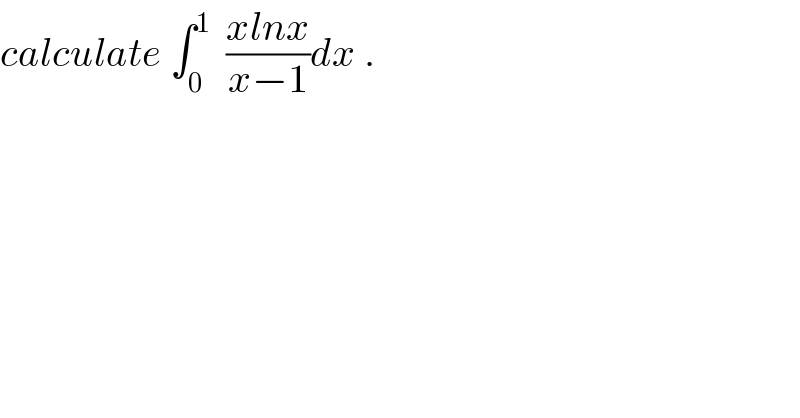
$${calculate}\:\int_{\mathrm{0}} ^{\mathrm{1}} \:\:\frac{{xlnx}}{{x}−\mathrm{1}}{dx}\:. \\ $$
Commented by math khazana by abdo last updated on 30/Apr/18
![I =∫_0 ^1 (((x−1+1))/(x−1))ln(x)dx = ∫_0 ^1 ln(x)x +∫_0 ^1 ((lnx)/(x−1))dx ∫_0 ^1 ln(x)dx=[xlnx −x]_(x→0) ^1 =−1 ∫_0 ^1 ((ln(x))/(x−1))dx=−∫_0 ^1 (Σ_(n=0) ^∞ x^n )ln(x)dx =−Σ_(n=0) ^∞ ∫_0 ^1 x^n ln(x)dx by parts A_n = ∫_0 ^1 x^n ln(x)dx=[(1/(n+1))x^(n+1) ln(x)]_0 ^1 −∫_0 ^1 (1/(n+1)) x^n dx =−(1/(n+1)) ∫_0 ^1 x^n dx=−(1/((n+1)^2 )) ⇒ ∫_0 ^1 ((xln(x))/(x−1))dx= −1+Σ_(n=0) ^∞ (1/((n+1)^2 )) =Σ_(n=1) ^∞ (1/n^2 )−1 ∫_0 ^1 ((xln(x))/(x−1))dx = (π^2 /6) −1 .](https://www.tinkutara.com/question/Q34057.png)
$${I}\:=\int_{\mathrm{0}} ^{\mathrm{1}} \:\:\frac{\left({x}−\mathrm{1}+\mathrm{1}\right)}{{x}−\mathrm{1}}{ln}\left({x}\right){dx}\:=\:\int_{\mathrm{0}} ^{\mathrm{1}} \:{ln}\left({x}\right){x}\:+\int_{\mathrm{0}} ^{\mathrm{1}} \:\frac{{lnx}}{{x}−\mathrm{1}}{dx} \\ $$$$\int_{\mathrm{0}} ^{\mathrm{1}} \:{ln}\left({x}\right){dx}=\left[{xlnx}\:−{x}\right]_{{x}\rightarrow\mathrm{0}} ^{\mathrm{1}} \:=−\mathrm{1} \\ $$$$\int_{\mathrm{0}} ^{\mathrm{1}} \:\:\frac{{ln}\left({x}\right)}{{x}−\mathrm{1}}{dx}=−\int_{\mathrm{0}} ^{\mathrm{1}} \left(\sum_{{n}=\mathrm{0}} ^{\infty} {x}^{{n}} \right){ln}\left({x}\right){dx} \\ $$$$=−\sum_{{n}=\mathrm{0}} ^{\infty} \:\:\int_{\mathrm{0}} ^{\mathrm{1}} \:{x}^{{n}} \:{ln}\left({x}\right){dx}\:\:{by}\:{parts} \\ $$$${A}_{{n}} =\:\int_{\mathrm{0}} ^{\mathrm{1}} \:{x}^{{n}} {ln}\left({x}\right){dx}=\left[\frac{\mathrm{1}}{{n}+\mathrm{1}}{x}^{{n}+\mathrm{1}} {ln}\left({x}\right)\right]_{\mathrm{0}} ^{\mathrm{1}} \\ $$$$−\int_{\mathrm{0}} ^{\mathrm{1}} \:\:\frac{\mathrm{1}}{{n}+\mathrm{1}}\:{x}^{{n}} {dx}\:=−\frac{\mathrm{1}}{{n}+\mathrm{1}}\:\int_{\mathrm{0}} ^{\mathrm{1}} \:{x}^{{n}} {dx}=−\frac{\mathrm{1}}{\left({n}+\mathrm{1}\right)^{\mathrm{2}} }\:\Rightarrow \\ $$$$\int_{\mathrm{0}} ^{\mathrm{1}} \:\:\frac{{xln}\left({x}\right)}{{x}−\mathrm{1}}{dx}=\:−\mathrm{1}+\sum_{{n}=\mathrm{0}} ^{\infty} \:\:\frac{\mathrm{1}}{\left({n}+\mathrm{1}\right)^{\mathrm{2}} }\:=\sum_{{n}=\mathrm{1}} ^{\infty} \:\frac{\mathrm{1}}{{n}^{\mathrm{2}} }−\mathrm{1}\: \\ $$$$\int_{\mathrm{0}} ^{\mathrm{1}} \:\:\:\frac{{xln}\left({x}\right)}{{x}−\mathrm{1}}{dx}\:=\:\frac{\pi^{\mathrm{2}} }{\mathrm{6}}\:−\mathrm{1}\:. \\ $$
