Question Number 34258 by math khazana by abdo last updated on 03/May/18
![1) prove that ∀ x∈]0,1[ 1−(1/x)≤lnx≤ x−1 2) find 2 sequences u_n and v_n / u_n ≤Π_(k=1) ^(n−1) ln((k/n))≤v_n ∀n≥2](https://www.tinkutara.com/question/Q34258.png)
$$\left.\mathrm{1}\left.\right)\:{prove}\:{that}\:\forall\:{x}\in\right]\mathrm{0},\mathrm{1}\left[\:\:\mathrm{1}−\frac{\mathrm{1}}{{x}}\leqslant{lnx}\leqslant\:{x}−\mathrm{1}\right. \\ $$$$\left.\mathrm{2}\right)\:{find}\:\mathrm{2}\:{sequences}\:{u}_{{n}} \:{and}\:{v}_{{n}} \:\:\:/ \\ $$$${u}_{{n}} \leqslant\prod_{{k}=\mathrm{1}} ^{{n}−\mathrm{1}} \:{ln}\left(\frac{{k}}{{n}}\right)\leqslant{v}_{{n}} \:\:\:\:\forall{n}\geqslant\mathrm{2} \\ $$
Commented by math khazana by abdo last updated on 03/May/18
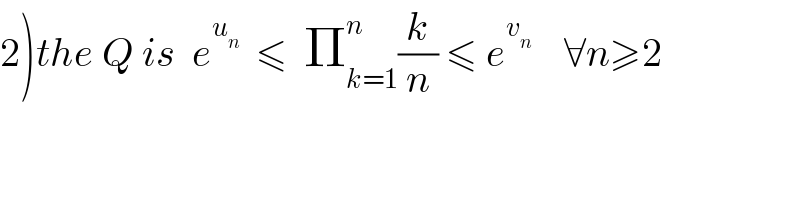
$$\left.\mathrm{2}\right){the}\:{Q}\:{is}\:\:{e}^{{u}_{{n}} } \:\:\leqslant\:\:\prod_{{k}=\mathrm{1}} ^{{n}} \frac{{k}}{{n}}\:\leqslant\:{e}^{{v}_{{n}} } \:\:\:\:\forall{n}\geqslant\mathrm{2} \\ $$
