Question Number 165955 by cortano1 last updated on 10/Feb/22
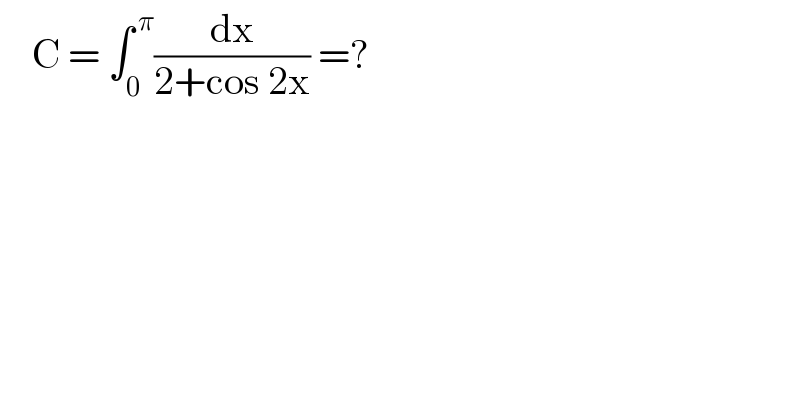
$$\:\:\:\:\mathrm{C}\:=\:\int_{\mathrm{0}} ^{\:\pi} \frac{\mathrm{dx}}{\mathrm{2}+\mathrm{cos}\:\mathrm{2x}}\:=? \\ $$
Answered by MJS_new last updated on 10/Feb/22
![∫_0 ^π (dx/(2+cos 2x))=2∫_0 ^(π/2) (dx/(2+cos 2x)) ∫(dx/(2+cos 2x))= [t=tan x → dx=(dt/(t^2 +1))] =∫(dt/(t^2 +3))=((√3)/3)arctan (((√3)t)/3) =((√3)/3)arctan (((√3)tan x)/3) +C ⇒ ∫_0 ^π (dx/(2+cos 2x))=(((√3)π)/3)](https://www.tinkutara.com/question/Q165960.png)
$$\underset{\mathrm{0}} {\overset{\pi} {\int}}\frac{{dx}}{\mathrm{2}+\mathrm{cos}\:\mathrm{2}{x}}=\mathrm{2}\underset{\mathrm{0}} {\overset{\pi/\mathrm{2}} {\int}}\frac{{dx}}{\mathrm{2}+\mathrm{cos}\:\mathrm{2}{x}} \\ $$$$\int\frac{{dx}}{\mathrm{2}+\mathrm{cos}\:\mathrm{2}{x}}= \\ $$$$\:\:\:\:\:\left[{t}=\mathrm{tan}\:{x}\:\rightarrow\:{dx}=\frac{{dt}}{{t}^{\mathrm{2}} +\mathrm{1}}\right] \\ $$$$=\int\frac{{dt}}{{t}^{\mathrm{2}} +\mathrm{3}}=\frac{\sqrt{\mathrm{3}}}{\mathrm{3}}\mathrm{arctan}\:\frac{\sqrt{\mathrm{3}}{t}}{\mathrm{3}}\:=\frac{\sqrt{\mathrm{3}}}{\mathrm{3}}\mathrm{arctan}\:\frac{\sqrt{\mathrm{3}}\mathrm{tan}\:{x}}{\mathrm{3}}\:+{C} \\ $$$$\Rightarrow \\ $$$$\underset{\mathrm{0}} {\overset{\pi} {\int}}\frac{{dx}}{\mathrm{2}+\mathrm{cos}\:\mathrm{2}{x}}=\frac{\sqrt{\mathrm{3}}\pi}{\mathrm{3}} \\ $$
