Question Number 101231 by 175 last updated on 01/Jul/20
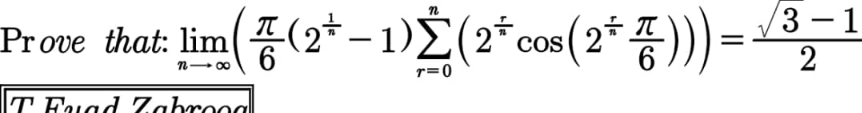
Commented by Dwaipayan Shikari last updated on 01/Jul/20
![(1/n).(π/6)lim_(n→∞) ((2^(1/n) −1)/(1/n)) Σ_(r=0) ^n (2^(r/n) cos(2^(r/n) (π/6))) (π/6) log2 ∫_0 ^1 2^x cos(2^x (π/6))dx ∫_0 ^1 cos(2^x (π/6))2^x (π/6)log2dx ∫_(π/6) ^(π/3) cost dt =[sint]_(π/6) ^(π/3) =(((√3)−1)/2) {suppose 2^x (π/6)=t}](https://www.tinkutara.com/question/Q101238.png)
$$\frac{\mathrm{1}}{{n}}.\frac{\pi}{\mathrm{6}}\underset{{n}\rightarrow\infty} {\mathrm{lim}}\frac{\mathrm{2}^{\frac{\mathrm{1}}{{n}}} −\mathrm{1}}{\frac{\mathrm{1}}{{n}}}\:\underset{{r}=\mathrm{0}} {\overset{{n}} {\sum}}\left(\mathrm{2}^{\frac{{r}}{{n}}} {cos}\left(\mathrm{2}^{\frac{{r}}{{n}}} \frac{\pi}{\mathrm{6}}\right)\right) \\ $$$$\frac{\pi}{\mathrm{6}}\:{log}\mathrm{2}\:\int_{\mathrm{0}} ^{\mathrm{1}} \mathrm{2}^{{x}} {cos}\left(\mathrm{2}^{{x}} \frac{\pi}{\mathrm{6}}\right){dx} \\ $$$$\int_{\mathrm{0}} ^{\mathrm{1}} {cos}\left(\mathrm{2}^{{x}} \frac{\pi}{\mathrm{6}}\right)\mathrm{2}^{{x}} \frac{\pi}{\mathrm{6}}{log}\mathrm{2}{dx} \\ $$$$\:\int_{\frac{\pi}{\mathrm{6}}} ^{\frac{\pi}{\mathrm{3}}} {cost}\:{dt}\:=\left[{sint}\right]_{\frac{\pi}{\mathrm{6}}} ^{\frac{\pi}{\mathrm{3}}} =\frac{\sqrt{\mathrm{3}}−\mathrm{1}}{\mathrm{2}} \\ $$$$\left\{{suppose}\:\mathrm{2}^{{x}} \frac{\pi}{\mathrm{6}}={t}\right\} \\ $$
Answered by smridha last updated on 01/Jul/20
![(𝛑/6)lim_(n→∞) ((2^(1/n) −1)/(1/n)).[lim_(n→∞) (1/n).Σ_(r=0) ^n 2^(r/n) .cos(2^(r/n) .(𝛑/6))] =(𝛑/6).ln(2).∫_(0 ) ^1 2^x .cos(2^x .(𝛑/6))dx =(𝛑/6).ln2.(6/(𝛑.ln(2)))∫_0 ^1 d[sin(2^x .(𝛑/6))] =1.[sin(2^x .(𝛑/6))]_0 ^1 =[sin(𝛑/3)−sin(𝛑/6)] =((√3)/2)−(1/2)=(((√3)−1)/2).](https://www.tinkutara.com/question/Q101236.png)
$$\frac{\boldsymbol{\pi}}{\mathrm{6}}\underset{\boldsymbol{{n}}\rightarrow\infty} {\mathrm{lim}}\frac{\mathrm{2}^{\frac{\mathrm{1}}{\boldsymbol{{n}}}} −\mathrm{1}}{\frac{\mathrm{1}}{\boldsymbol{{n}}}}.\left[\underset{\boldsymbol{{n}}\rightarrow\infty} {\mathrm{lim}}\frac{\mathrm{1}}{\boldsymbol{{n}}}.\underset{\boldsymbol{{r}}=\mathrm{0}} {\overset{\boldsymbol{{n}}} {\sum}}\mathrm{2}^{\frac{\boldsymbol{{r}}}{\boldsymbol{{n}}}} .\boldsymbol{{cos}}\left(\mathrm{2}^{\frac{\boldsymbol{{r}}}{\boldsymbol{{n}}}} .\frac{\boldsymbol{\pi}}{\mathrm{6}}\right)\right] \\ $$$$=\frac{\boldsymbol{\pi}}{\mathrm{6}}.\boldsymbol{{ln}}\left(\mathrm{2}\right).\int_{\mathrm{0}\:} ^{\mathrm{1}} \mathrm{2}^{\boldsymbol{{x}}} .\boldsymbol{{cos}}\left(\mathrm{2}^{\boldsymbol{{x}}} .\frac{\boldsymbol{\pi}}{\mathrm{6}}\right)\boldsymbol{{dx}} \\ $$$$=\frac{\boldsymbol{\pi}}{\mathrm{6}}.\boldsymbol{{ln}}\mathrm{2}.\frac{\mathrm{6}}{\boldsymbol{\pi}.\boldsymbol{{ln}}\left(\mathrm{2}\right)}\int_{\mathrm{0}} ^{\mathrm{1}} \boldsymbol{{d}}\left[\boldsymbol{{sin}}\left(\mathrm{2}^{\boldsymbol{{x}}} .\frac{\boldsymbol{\pi}}{\mathrm{6}}\right)\right] \\ $$$$=\mathrm{1}.\left[\boldsymbol{{sin}}\left(\mathrm{2}^{\boldsymbol{{x}}} .\frac{\boldsymbol{\pi}}{\mathrm{6}}\right)\right]_{\mathrm{0}} ^{\mathrm{1}} =\left[\boldsymbol{{sin}}\frac{\boldsymbol{\pi}}{\mathrm{3}}−\boldsymbol{{sin}}\frac{\boldsymbol{\pi}}{\mathrm{6}}\right] \\ $$$$\:\:\:\:=\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}−\frac{\mathrm{1}}{\mathrm{2}}=\frac{\sqrt{\mathrm{3}}−\mathrm{1}}{\mathrm{2}}. \\ $$
Commented by 175 last updated on 01/Jul/20
thanx
Commented by smridha last updated on 01/Jul/20
welcome...but careful there is a group
��������
