Menu Close

Multiple-Choice-Questions-Rio-Mike-Q-1-The-value-of-6-2-4-15-3-is-A-3-B-9-C-4-D-27-Q-2-80-as-a-product-of-its-prime-factor-is-A-2-3-5-B-2-5-3-C-2-2-5-2-D-2-4-

Tinku Tara 0 Comments
Pin




Question Number 35811 by Rio Mike last updated on 23/May/18
Multiple Choice Questions Rio Mike. Q_1 . The value of 6 + 2 × 4 −15 ÷ 3 is; A) 3 B) 9 C) 4 D) 27 Q_2 . 80 as a product of its prime factor is. A) 2^3 × 5 B) 2 × 5^(3 ) C) 2^2 × 5^2 D) 2^4 × 5 Q_3 . The deteminant of (((6 4)),((3 2)) ) is A) 18 B) 0 C) 24 D) −24 Q_4 . the value of ((1/(16)))^(−(1/2)) is A) −(1/4) B) 4 C) −4 D) (1/2) Q_5 . if −8,m,n,19 are in AP then (m,n) is A) (1,10) B) (2,10) C) (3,13) D) (4,16)o Q_6 . if cos θ = ((12)/(13)) then cot^2 θ is; A) ((169)/(25)) B) ((25)/(169)) C)((169)/(144)) D) ((144)/(169)) Q_7 . the solution set of 3 ≤ 2x−1≤5 is; A) ]x≥−2,x≤(8/3)[ B) [x≥2,x≤−(8/3)[ C) ]x>−2,x≤(3/8)] D) [x≥−2,x≤(8/3)] Q_8 . Which is a factor of f(x)= x^2 −3x + 2 A) (x−1) B) (x−2) C) (x+1) D)(x+3) Q_(9 ) . The sum of the sum of roots and product of roots of the quadratic equation 3x^2 + 6x + 9=0 A) 1 B) −1 C) 32 D) 5 Q_(10) . 2log2−log2 = A) log 8 B) log 6 C) log 3 D) log 2. Q_(11) . Σ_(r=1) ^∞ 3^(2−r) = A) (9/4) B) (9/2) C) ((13)/3) D) (1/2) Q_(12) . The constand term in the binomial expansion of (x^2 + (1/x^2 ))^8 is A) 3^(rd) B) 4^(th) C) 5^(th) D) 6^(th) Q_(13) . cos(180−x) = A) −sinx B) sin x C) cos x D) −cos x Q_(14) . The value of p for which (2,1) , (6,3), and (4,p) are collinear is ; A) 2 B) 1 C)−1 D) −2 Q_(15) . ∫_1 ^2 x^3 dx = A) −sin 7x B) sin 7x C) −7sin7x D) 7sin7x Q_(16) . Given that g : → px −5, the value of p for which g^(−1) (3)=4 is A) (1/2) B) −(1/2) C) −2 D) 2 Q_(17) . The value of θ in the range 0°≤θ≤90° for which sinθ = cos θ is A) 90° B) 60° C) 30° D) 45° Questions
$$\:{Multiple}\:{Choice}\:{Questions} \\ $$$$\:\:\:\boldsymbol{{Rio}}\:\boldsymbol{{M}}{ike}. \\ $$$$ \\ $$$${Q}_{\mathrm{1}} .\:{The}\:{value}\:{of}\:\:\mathrm{6}\:+\:\mathrm{2}\:×\:\mathrm{4}\:−\mathrm{15}\:\boldsymbol{\div}\:\mathrm{3} \\ $$$${is}; \\ $$$$\left.{A}\left.\right)\left.\:\left.\mathrm{3}\:\:{B}\right)\:\mathrm{9}\:{C}\right)\:\mathrm{4}\:{D}\right)\:\mathrm{27} \\ $$$$ \\ $$$${Q}_{\mathrm{2}} .\:\mathrm{80}\:{as}\:{a}\:{product}\:{of}\:{its}\:{prime} \\ $$$${factor}\:{is}. \\ $$$$\left.{A}\left.\right)\left.\:\mathrm{2}^{\mathrm{3}} ×\:\mathrm{5}\:{B}\right)\:\mathrm{2}\:×\:\mathrm{5}^{\mathrm{3}\:} \:{C}\right)\:\mathrm{2}^{\mathrm{2}} ×\:\mathrm{5}^{\mathrm{2}} \\ $$$$\left.{D}\right)\:\mathrm{2}^{\mathrm{4}} ×\:\mathrm{5} \\ $$$$ \\ $$$${Q}_{\mathrm{3}} .\:{The}\:{deteminant}\:{of}\:\:\begin{pmatrix}{\mathrm{6}\:\:\:\:\:\:\:\:\:\mathrm{4}}\\{\mathrm{3}\:\:\:\:\:\:\:\:\:\:\mathrm{2}}\end{pmatrix}\:{is} \\ $$$$\left.{A}\left.\right)\left.\:\left.\mathrm{18}\:\:{B}\right)\:\mathrm{0}\:\:{C}\right)\:\mathrm{24}\:{D}\right)\:−\mathrm{24} \\ $$$$ \\ $$$${Q}_{\mathrm{4}} .\:{the}\:{value}\:{of}\:\left(\frac{\mathrm{1}}{\mathrm{16}}\right)^{−\frac{\mathrm{1}}{\mathrm{2}}} {is} \\ $$$$\left.{A}\left.\right)\left.\:\left.−\frac{\mathrm{1}}{\mathrm{4}}\:\:\:{B}\right)\:\mathrm{4}\:\:\:{C}\right)\:−\mathrm{4}\:\:\:\:{D}\right)\:\frac{\mathrm{1}}{\mathrm{2}} \\ $$$$ \\ $$$${Q}_{\mathrm{5}} .\:{if}\:−\mathrm{8},{m},{n},\mathrm{19}\:{are}\:{in}\:{AP}\:{then}\: \\ $$$$\left({m},{n}\right)\:{is}\: \\ $$$$\left.{A}\left.\right)\left.\:\left.\left(\mathrm{1},\mathrm{10}\right)\:{B}\right)\:\left(\mathrm{2},\mathrm{10}\right)\:{C}\right)\:\left(\mathrm{3},\mathrm{13}\right)\:{D}\right)\:\left(\mathrm{4},\mathrm{16}\right){o} \\ $$$$ \\ $$$${Q}_{\mathrm{6}} .\:{if}\:{cos}\:\theta\:=\:\frac{\mathrm{12}}{\mathrm{13}}\:{then}\:{cot}^{\mathrm{2}} \theta\:{is}; \\ $$$$\left.{A}\left.\right)\left.\:\left.\frac{\mathrm{169}}{\mathrm{25}}\:\:{B}\right)\:\frac{\mathrm{25}}{\mathrm{169}}\:{C}\right)\frac{\mathrm{169}}{\mathrm{144}}\:{D}\right)\:\frac{\mathrm{144}}{\mathrm{169}} \\ $$$$ \\ $$$${Q}_{\mathrm{7}} .\:{the}\:{solution}\:{set}\:{of}\:\mathrm{3}\:\leqslant\:\mathrm{2}{x}−\mathrm{1}\leqslant\mathrm{5} \\ $$$${is};\: \\ $$$$\left.{A}\left.\right)\:\right]{x}\geqslant−\mathrm{2},{x}\leqslant\frac{\mathrm{8}}{\mathrm{3}}\left[\:\:\:{B}\right)\:\left[{x}\geqslant\mathrm{2},{x}\leqslant−\frac{\mathrm{8}}{\mathrm{3}}\left[\right.\right. \\ $$$$\left.{C}\left.\right)\left.\:\left.\right]{x}>−\mathrm{2},{x}\leqslant\frac{\mathrm{3}}{\mathrm{8}}\right]\:\:{D}\right)\:\left[{x}\geqslant−\mathrm{2},{x}\leqslant\frac{\mathrm{8}}{\mathrm{3}}\right] \\ $$$$ \\ $$$${Q}_{\mathrm{8}} .\:{Which}\:{is}\:{a}\:{factor}\:{of}\:{f}\left({x}\right)=\: \\ $$$${x}^{\mathrm{2}} −\mathrm{3}{x}\:+\:\mathrm{2} \\ $$$$\left.{A}\left.\right)\left.\:\left.\left({x}−\mathrm{1}\right)\:{B}\right)\:\left({x}−\mathrm{2}\right)\:{C}\right)\:\left({x}+\mathrm{1}\right)\:{D}\right)\left({x}+\mathrm{3}\right) \\ $$$$ \\ $$$${Q}_{\mathrm{9}\:} .\:{The}\:{sum}\:{of}\:{the}\:{sum}\:{of}\: \\ $$$${roots}\:{and}\:{product}\:{of}\:{roots}\:{of}\:{the} \\ $$$${quadratic}\:{equation}\:\mathrm{3}{x}^{\mathrm{2}} +\:\mathrm{6}{x}\:+\:\mathrm{9}=\mathrm{0} \\ $$$$\left.{A}\left.\right)\left.\:\left.\mathrm{1}\:\:\:{B}\right)\:−\mathrm{1}\:\:{C}\right)\:\mathrm{32}\:\:{D}\right)\:\mathrm{5} \\ $$$$ \\ $$$${Q}_{\mathrm{10}} .\:\mathrm{2}{log}\mathrm{2}−{log}\mathrm{2}\:=\: \\ $$$$\left.{A}\left.\right)\left.\:{log}\:\mathrm{8}\:\:\:\:\:\:\:{B}\right)\:{log}\:\mathrm{6}\:\:\:\:{C}\right)\:{log}\:\mathrm{3} \\ $$$$\left.{D}\right)\:{log}\:\mathrm{2}. \\ $$$$ \\ $$$${Q}_{\mathrm{11}} .\:\underset{{r}=\mathrm{1}} {\overset{\infty} {\sum}}\mathrm{3}^{\mathrm{2}−{r}} = \\ $$$$\left.{A}\left.\right)\left.\:\left.\frac{\mathrm{9}}{\mathrm{4}}\:\:{B}\right)\:\frac{\mathrm{9}}{\mathrm{2}}\:\:{C}\right)\:\frac{\mathrm{13}}{\mathrm{3}}\:{D}\right)\:\frac{\mathrm{1}}{\mathrm{2}} \\ $$$$ \\ $$$${Q}_{\mathrm{12}} .\:{The}\:{constand}\:{term}\:{in}\:{the}\: \\ $$$${binomial}\:{expansion}\:{of}\:\left({x}^{\mathrm{2}} +\:\frac{\mathrm{1}}{{x}^{\mathrm{2}} }\right)^{\mathrm{8}} {is} \\ $$$$\left.{A}\left.\right)\left.\:\left.\mathrm{3}^{{rd}} \:\:{B}\right)\:\mathrm{4}^{{th}} \:{C}\right)\:\mathrm{5}^{{th}} \:{D}\right)\:\mathrm{6}^{{th}} \: \\ $$$$ \\ $$$${Q}_{\mathrm{13}} .\:{cos}\left(\mathrm{180}−{x}\right)\:=\: \\ $$$$\left.{A}\left.\right)\left.\:−{sinx}\:\:\:{B}\right)\:{sin}\:{x}\:\:{C}\right)\:{cos}\:{x}\: \\ $$$$\left.{D}\right)\:−{cos}\:{x} \\ $$$$ \\ $$$${Q}_{\mathrm{14}} .\:{The}\:{value}\:{of}\:{p}\:{for}\:{which}\: \\ $$$$\left(\mathrm{2},\mathrm{1}\right)\:,\:\left(\mathrm{6},\mathrm{3}\right),\:{and}\:\left(\mathrm{4},{p}\right)\:{are}\:{collinear} \\ $$$${is}\:; \\ $$$$\left.{A}\left.\right)\left.\:\left.\mathrm{2}\:\:{B}\right)\:\mathrm{1}\:{C}\right)−\mathrm{1}\:{D}\right)\:−\mathrm{2} \\ $$$$ \\ $$$${Q}_{\mathrm{15}} .\:\int_{\mathrm{1}} ^{\mathrm{2}} {x}^{\mathrm{3}} {dx}\:=\: \\ $$$$\left.{A}\left.\right)\left.\:−{sin}\:\mathrm{7}{x}\:\:\:{B}\right)\:{sin}\:\mathrm{7}{x}\:\:{C}\right)\:−\mathrm{7}{sin}\mathrm{7}{x} \\ $$$$\left.{D}\right)\:\mathrm{7}{sin}\mathrm{7}{x} \\ $$$$ \\ $$$${Q}_{\mathrm{16}} .\:{Given}\:{that}\:{g}\::\:\rightarrow\:{px}\:−\mathrm{5},\:{the}\: \\ $$$${value}\:{of}\:{p}\:{for}\:{which}\:{g}^{−\mathrm{1}} \left(\mathrm{3}\right)=\mathrm{4}\:{is} \\ $$$$\left.{A}\left.\right)\left.\:\left.\frac{\mathrm{1}}{\mathrm{2}}\:{B}\right)\:−\frac{\mathrm{1}}{\mathrm{2}}\:{C}\right)\:−\mathrm{2}\:\:{D}\right)\:\mathrm{2} \\ $$$$ \\ $$$${Q}_{\mathrm{17}} .\:{The}\:{value}\:{of}\:\theta\:{in}\:{the}\:{range}\: \\ $$$$\mathrm{0}°\leqslant\theta\leqslant\mathrm{90}°\:{for}\:{which}\:{sin}\theta\:=\:{cos}\:\theta\:{is} \\ $$$$\left.{A}\left.\right)\left.\:\left.\mathrm{90}°\:\:{B}\right)\:\mathrm{60}°\:{C}\right)\:\mathrm{30}°\:{D}\right)\:\mathrm{45}°\: \\ $$$$ \\ $$$$\:{Questions}\: \\ $$
Commented by Rasheed.Sindhi last updated on 24/May/18
How did you upload so large image?!
$$\mathrm{How}\:\mathrm{did}\:\mathrm{you}\:\mathrm{upload}\:\mathrm{so}\:\mathrm{large}\:\mathrm{image}?! \\ $$
Commented by Joel579 last updated on 24/May/18
Actually he typed it, not uploaded it
$$\mathrm{Actually}\:\mathrm{he}\:\mathrm{typed}\:\mathrm{it},\:\mathrm{not}\:\mathrm{uploaded}\:\mathrm{it} \\ $$
Commented by Rasheed.Sindhi last updated on 24/May/18
Sir I misunderstood.But his other uploaded lengthy post is an image.
$$\mathrm{Sir}\:\mathrm{I}\:\mathrm{misunderstood}.\mathrm{But}\:\mathrm{his}\:\mathrm{other}\: \\ $$$$\mathrm{uploaded}\:\mathrm{lengthy}\:\mathrm{post}\:\mathrm{is}\:\mathrm{an}\:\mathrm{image}. \\ $$
Commented by Rio Mike last updated on 24/May/18
yeah your right . i typed this but the other was uploaded as an image
$$\mathrm{yeah}\:\mathrm{your}\:\mathrm{right}\:.\:\mathrm{i}\:\mathrm{typed}\:\mathrm{this}\:\mathrm{but} \\ $$$$\mathrm{the}\:\mathrm{other}\:\mathrm{was}\:\mathrm{uploaded}\:{as}\:{an}\:{image} \\ $$
Commented by Rasheed.Sindhi last updated on 25/May/18
Questioners are requested to send at most (3 short questions)/post or (1 long question)/post It′s better practice, I think.
$$\boldsymbol{\mathrm{Questioners}}\:\boldsymbol{\mathrm{are}}\:\boldsymbol{\mathrm{requested}}\:\boldsymbol{\mathrm{to}}\:\boldsymbol{\mathrm{send}}\:\boldsymbol{\mathrm{at}}\:\boldsymbol{\mathrm{most}} \\ $$$$\left(\mathrm{3}\:\mathrm{short}\:\mathrm{questions}\right)/\mathrm{post} \\ $$$$\boldsymbol{\mathrm{or}} \\ $$$$\left(\mathrm{1}\:\mathrm{long}\:\mathrm{question}\right)/\mathrm{post} \\ $$$$\boldsymbol{\mathrm{It}}'\boldsymbol{\mathrm{s}}\:\boldsymbol{\mathrm{better}}\:\boldsymbol{\mathrm{practice}},\:\boldsymbol{\mathrm{I}}\:\boldsymbol{\mathrm{think}}. \\ $$
Commented by rahul 19 last updated on 26/May/18
I agree.
$${I}\:{agree}. \\ $$
Answered by Rasheed.Sindhi last updated on 25/May/18
Q_1 6 + 2 × 4 −15 ÷ 3 =6+8−5=9 B) 9 Q_2 D) 2^4 .5 Q_3 The deteminant of (((6 4)),((3 2)) ) 6×2−3×4=0 B) 0 Q_4 ((1/(16)))^(−(1/2)) =(1/((4^2 )^(−(1/2)) ))=(1/4^(−1) )=4 B) 4 Q_5 −8,m,n,19 are in AP First term=a=−8, Common difference=d nthterm=a_n =a+(n−1)d a_4 =−8+(4−1)d=19 3d=19+8=27 d=9 m=−8+9=1,n=1+9=10 (m,n)=(1,10) A) (1,10)
$$\mathrm{Q}_{\mathrm{1}} \\ $$$$\:\:\:\:\mathrm{6}\:+\:\mathrm{2}\:×\:\mathrm{4}\:−\mathrm{15}\:\boldsymbol{\div}\:\mathrm{3} \\ $$$$\:\:\:\:\:\:\:=\mathrm{6}+\mathrm{8}−\mathrm{5}=\mathrm{9} \\ $$$$\left.\mathrm{B}\right)\:\mathrm{9} \\ $$$$\mathrm{Q}_{\mathrm{2}} \\ $$$$\left.\mathrm{D}\right)\:\:\:\mathrm{2}^{\mathrm{4}} .\mathrm{5} \\ $$$$\mathrm{Q}_{\mathrm{3}} \:\:\:{The}\:{deteminant}\:{of}\:\:\begin{pmatrix}{\mathrm{6}\:\:\:\:\:\:\:\:\:\mathrm{4}}\\{\mathrm{3}\:\:\:\:\:\:\:\:\:\:\mathrm{2}}\end{pmatrix}\: \\ $$$$\:\:\:\:\:\:\:\:\:\mathrm{6}×\mathrm{2}−\mathrm{3}×\mathrm{4}=\mathrm{0} \\ $$$$\left.\:\:\:\:\mathrm{B}\right)\:\:\:\mathrm{0} \\ $$$$\mathrm{Q}_{\mathrm{4}} \:\:\left(\frac{\mathrm{1}}{\mathrm{16}}\right)^{−\frac{\mathrm{1}}{\mathrm{2}}} \\ $$$$\:\:\:\:\:\:=\frac{\mathrm{1}}{\left(\mathrm{4}^{\mathrm{2}} \right)^{−\frac{\mathrm{1}}{\mathrm{2}}} }=\frac{\mathrm{1}}{\mathrm{4}^{−\mathrm{1}} }=\mathrm{4} \\ $$$$\left.\mathrm{B}\right)\:\mathrm{4} \\ $$$$\mathrm{Q}_{\mathrm{5}} \:−\mathrm{8},\mathrm{m},\mathrm{n},\mathrm{19}\:\mathrm{are}\:\mathrm{in}\:\mathrm{AP} \\ $$$$\mathrm{First}\:\mathrm{term}={a}=−\mathrm{8},\:\mathrm{Common}\:\mathrm{difference}={d} \\ $$$${nth}\mathrm{term}={a}_{{n}} ={a}+\left({n}−\mathrm{1}\right){d} \\ $$$$\:\:\:\:\:\:\:\:{a}_{\mathrm{4}} =−\mathrm{8}+\left(\mathrm{4}−\mathrm{1}\right){d}=\mathrm{19} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\mathrm{3}{d}=\mathrm{19}+\mathrm{8}=\mathrm{27} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:{d}=\mathrm{9} \\ $$$${m}=−\mathrm{8}+\mathrm{9}=\mathrm{1},{n}=\mathrm{1}+\mathrm{9}=\mathrm{10} \\ $$$$\left({m},{n}\right)=\left(\mathrm{1},\mathrm{10}\right) \\ $$$$\left.\mathrm{A}\right)\:\:\left(\mathrm{1},\mathrm{10}\right) \\ $$
Answered by Rasheed.Sindhi last updated on 25/May/18
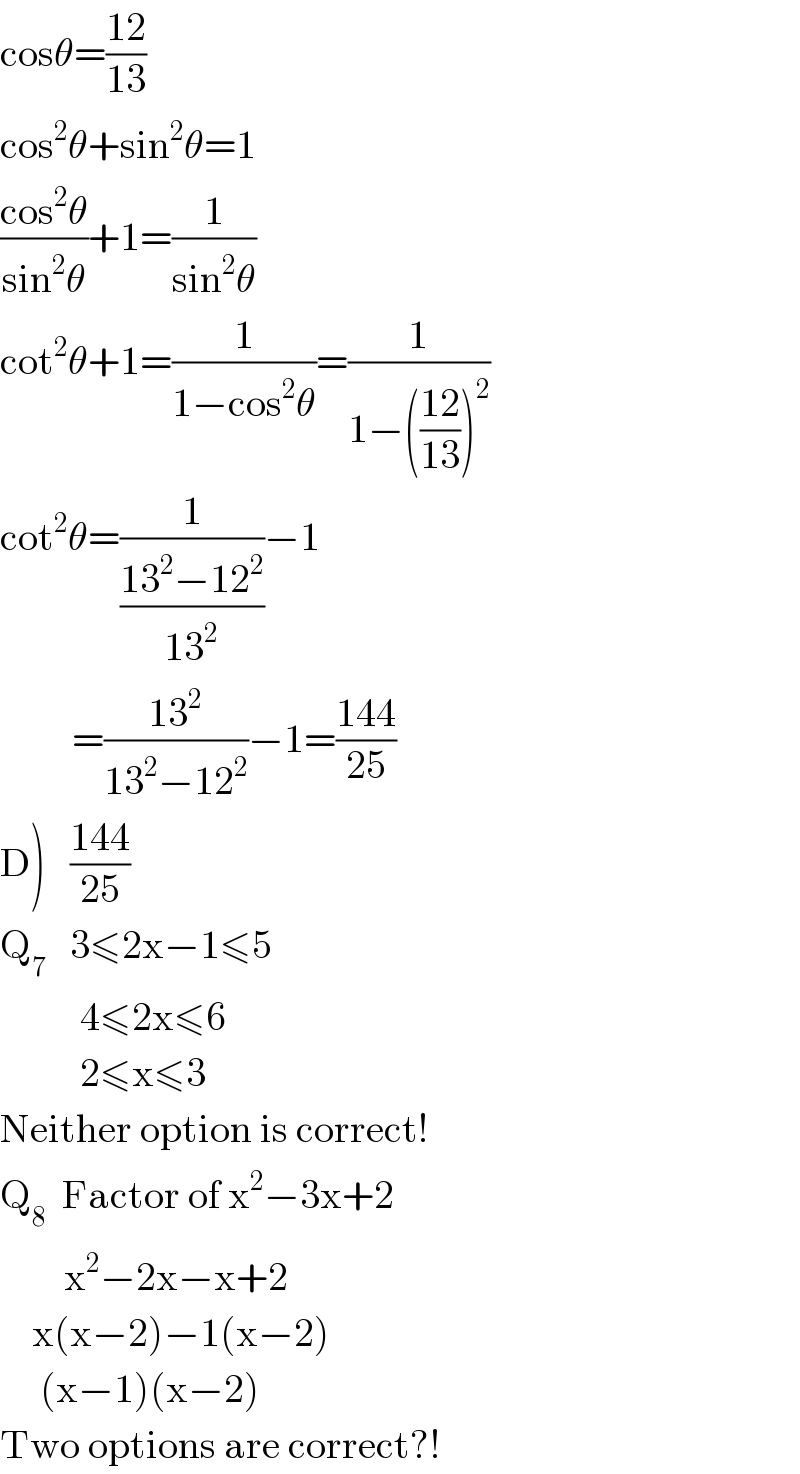
cosθ=((12)/(13)) cos^2 θ+sin^2 θ=1 ((cos^2 θ)/(sin^2 θ))+1=(1/(sin^2 θ)) cot^2 θ+1=(1/(1−cos^2 θ))=(1/(1−(((12)/(13)))^2 )) cot^2 θ=(1/((13^2 −12^2 )/(13^2 )))−1 =((13^2 )/(13^2 −12^2 ))−1=((144)/(25)) D) ((144)/(25)) Q_7 3≤2x−1≤5 4≤2x≤6 2≤x≤3 Neither option is correct! Q_8 Factor of x^2 −3x+2 x^2 −2x−x+2 x(x−2)−1(x−2) (x−1)(x−2) Two options are correct?!
$$\mathrm{cos}\theta=\frac{\mathrm{12}}{\mathrm{13}} \\ $$$$\mathrm{cos}^{\mathrm{2}} \theta+\mathrm{sin}^{\mathrm{2}} \theta=\mathrm{1} \\ $$$$\frac{\mathrm{cos}^{\mathrm{2}} \theta}{\mathrm{sin}^{\mathrm{2}} \theta}+\mathrm{1}=\frac{\mathrm{1}}{\mathrm{sin}^{\mathrm{2}} \theta} \\ $$$$\mathrm{cot}^{\mathrm{2}} \theta+\mathrm{1}=\frac{\mathrm{1}}{\mathrm{1}−\mathrm{cos}^{\mathrm{2}} \theta}=\frac{\mathrm{1}}{\mathrm{1}−\left(\frac{\mathrm{12}}{\mathrm{13}}\right)^{\mathrm{2}} } \\ $$$$\mathrm{cot}^{\mathrm{2}} \theta=\frac{\mathrm{1}}{\frac{\mathrm{13}^{\mathrm{2}} −\mathrm{12}^{\mathrm{2}} }{\mathrm{13}^{\mathrm{2}} }}−\mathrm{1} \\ $$$$\:\:\:\:\:\:\:\:\:=\frac{\mathrm{13}^{\mathrm{2}} }{\mathrm{13}^{\mathrm{2}} −\mathrm{12}^{\mathrm{2}} }−\mathrm{1}=\frac{\mathrm{144}}{\mathrm{25}} \\ $$$$\left.\mathrm{D}\right)\:\:\:\frac{\mathrm{144}}{\mathrm{25}} \\ $$$$\mathrm{Q}_{\mathrm{7}} \:\:\:\mathrm{3}\leqslant\mathrm{2x}−\mathrm{1}\leqslant\mathrm{5} \\ $$$$\:\:\:\:\:\:\:\:\:\:\mathrm{4}\leqslant\mathrm{2x}\leqslant\mathrm{6} \\ $$$$\:\:\:\:\:\:\:\:\:\:\mathrm{2}\leqslant\mathrm{x}\leqslant\mathrm{3} \\ $$$$\mathrm{Neither}\:\mathrm{option}\:\mathrm{is}\:\mathrm{correct}! \\ $$$$\mathrm{Q}_{\mathrm{8}} \:\:\mathrm{Factor}\:\mathrm{of}\:\mathrm{x}^{\mathrm{2}} −\mathrm{3x}+\mathrm{2} \\ $$$$\:\:\:\:\:\:\:\:\mathrm{x}^{\mathrm{2}} −\mathrm{2x}−\mathrm{x}+\mathrm{2} \\ $$$$\:\:\:\:\mathrm{x}\left(\mathrm{x}−\mathrm{2}\right)−\mathrm{1}\left(\mathrm{x}−\mathrm{2}\right) \\ $$$$\:\:\:\:\:\left(\mathrm{x}−\mathrm{1}\right)\left(\mathrm{x}−\mathrm{2}\right) \\ $$$$\mathrm{Two}\:\mathrm{options}\:\mathrm{are}\:\mathrm{correct}?! \\ $$
Answered by Rasheed.Sindhi last updated on 26/May/18
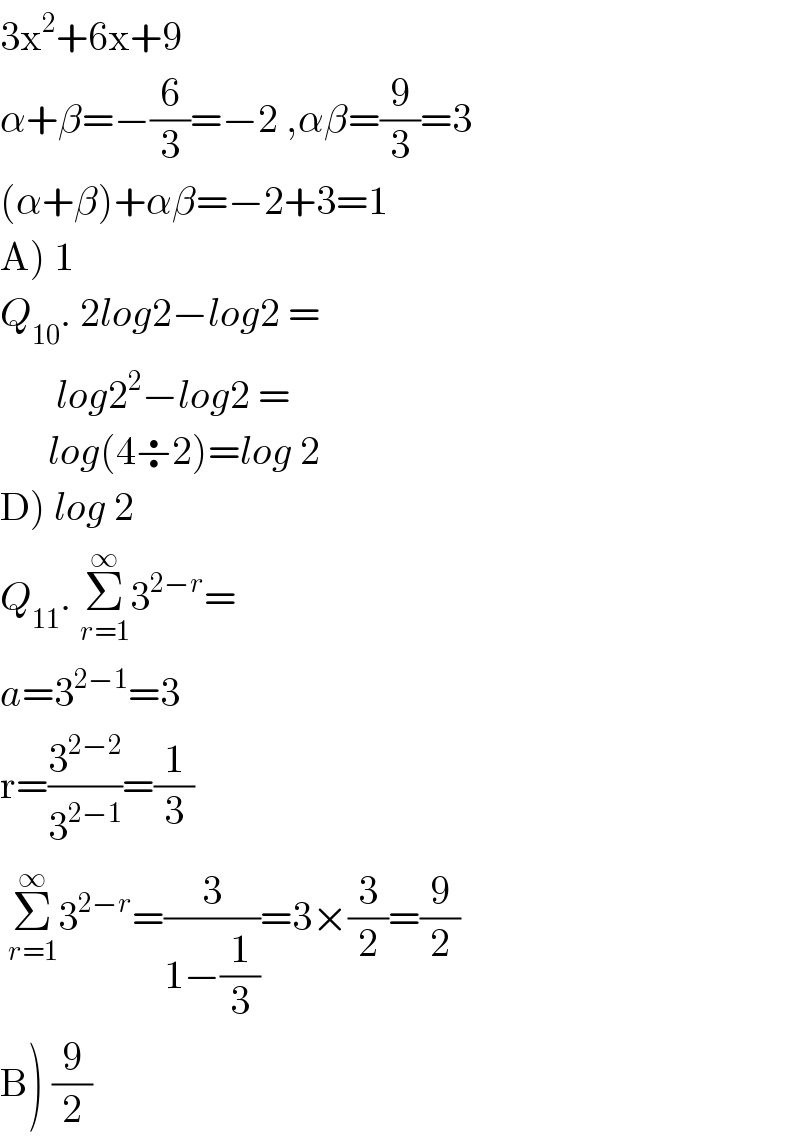
3x^2 +6x+9 α+β=−(6/3)=−2 ,αβ=(9/3)=3 (α+β)+αβ=−2+3=1 A) 1 Q_(10) . 2log2−log2 = log2^2 −log2 = log(4÷2)=log 2 D) log 2 Q_(11) . Σ_(r=1) ^∞ 3^(2−r) = a=3^(2−1) =3 r=(3^(2−2) /3^(2−1) )=(1/3) Σ_(r=1) ^∞ 3^(2−r) =(3/(1−(1/3)))=3×(3/2)=(9/2) B) (9/2)
$$\mathrm{3x}^{\mathrm{2}} +\mathrm{6x}+\mathrm{9} \\ $$$$\alpha+\beta=−\frac{\mathrm{6}}{\mathrm{3}}=−\mathrm{2}\:,\alpha\beta=\frac{\mathrm{9}}{\mathrm{3}}=\mathrm{3} \\ $$$$\left(\alpha+\beta\right)+\alpha\beta=−\mathrm{2}+\mathrm{3}=\mathrm{1} \\ $$$$\left.\mathrm{A}\right)\:\mathrm{1} \\ $$$${Q}_{\mathrm{10}} .\:\mathrm{2}{log}\mathrm{2}−{log}\mathrm{2}\:=\: \\ $$$$\:\:\:\:\:\:\:{log}\mathrm{2}^{\mathrm{2}} −{log}\mathrm{2}\:=\: \\ $$$$\:\:\:\:\:\:{log}\left(\mathrm{4}\boldsymbol{\div}\mathrm{2}\right)={log}\:\mathrm{2} \\ $$$$\left.\mathrm{D}\right)\:{log}\:\mathrm{2} \\ $$$${Q}_{\mathrm{11}} .\:\underset{{r}=\mathrm{1}} {\overset{\infty} {\sum}}\mathrm{3}^{\mathrm{2}−{r}} = \\ $$$${a}=\mathrm{3}^{\mathrm{2}−\mathrm{1}} =\mathrm{3} \\ $$$$\mathrm{r}=\frac{\mathrm{3}^{\mathrm{2}−\mathrm{2}} }{\mathrm{3}^{\mathrm{2}−\mathrm{1}} }=\frac{\mathrm{1}}{\mathrm{3}} \\ $$$$\:\underset{{r}=\mathrm{1}} {\overset{\infty} {\sum}}\mathrm{3}^{\mathrm{2}−{r}} =\frac{\mathrm{3}}{\mathrm{1}−\frac{\mathrm{1}}{\mathrm{3}}}=\mathrm{3}×\frac{\mathrm{3}}{\mathrm{2}}=\frac{\mathrm{9}}{\mathrm{2}} \\ $$$$\left.\mathrm{B}\right)\:\frac{\mathrm{9}}{\mathrm{2}} \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *