Question Number 35873 by Tinkutara last updated on 25/May/18
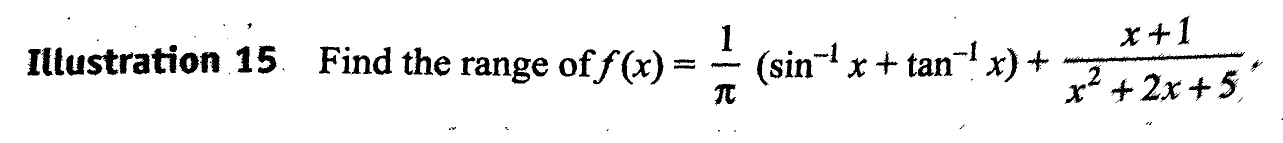
Answered by tanmay.chaudhury50@gmail.com last updated on 28/May/18
![let sin^(−1) x=θ sinθ=x tanθ=(x/( (√(1−x^2 )))) so θ=tan^(−1) ((x/( (√(1−x^2 ))))) f(x)=(1/Π){tan^(−1) ((x/( (√(1−x^2 )))))+tan^(−1) x}+((x+1)/((x+1)^2 +4)) f(x)=(1/Π){tan^(−1) ((((x/( (√(1−x^(2 ) ))))+(x/1))/(1−(x^2 /( (√(1−x^2 )))))))}+((x+1)/((x+1)^2 +4)) f(x)=(1/Π){tan^(−1) (((x+x(√(1−x^2 )) )/( (√(1−x^2 )) −x^2 )))}+((x+1)/((x+1)^2 +4)) (1−x^2 )=(1+x)(1−x) 1−x^2 =0 at x=±1 1−x^2 <0 when x>1 1−x^2 <0 when x<−1 1−x^2 >0 when x [−1,1] ∣f(x)∣_(x=−1) =(1/Π){tan^− (1)}+0 =(1/4) f(x) at x=1 f(x)=(1/Π){tan^(−1) (−1)}+(2/8) =(1/Π)×−(Π/4)+(1/4) =0 range of f(x) [0,(1/4)] pls check pls](https://www.tinkutara.com/question/Q36090.png)
$${let}\:{sin}^{−\mathrm{1}} {x}=\theta \\ $$$${sin}\theta={x} \\ $$$${tan}\theta=\frac{{x}}{\:\sqrt{\mathrm{1}−{x}^{\mathrm{2}} }}\:\:\:{so}\:\theta={tan}^{−\mathrm{1}} \left(\frac{{x}}{\:\sqrt{\mathrm{1}−{x}^{\mathrm{2}} }}\right) \\ $$$${f}\left({x}\right)=\frac{\mathrm{1}}{\Pi}\left\{{tan}^{−\mathrm{1}} \left(\frac{{x}}{\:\sqrt{\mathrm{1}−{x}^{\mathrm{2}} }}\right)+{tan}^{−\mathrm{1}} {x}\right\}+\frac{{x}+\mathrm{1}}{\left({x}+\mathrm{1}\right)^{\mathrm{2}} +\mathrm{4}} \\ $$$${f}\left({x}\right)=\frac{\mathrm{1}}{\Pi}\left\{{tan}^{−\mathrm{1}} \left(\frac{\frac{{x}}{\:\sqrt{\mathrm{1}−{x}^{\mathrm{2}\:} }}+\frac{{x}}{\mathrm{1}}}{\mathrm{1}−\frac{{x}^{\mathrm{2}} }{\:\sqrt{\mathrm{1}−{x}^{\mathrm{2}} }}}\right)\right\}+\frac{{x}+\mathrm{1}}{\left({x}+\mathrm{1}\right)^{\mathrm{2}} +\mathrm{4}} \\ $$$${f}\left({x}\right)=\frac{\mathrm{1}}{\Pi}\left\{{tan}^{−\mathrm{1}} \left(\frac{{x}+{x}\sqrt{\mathrm{1}−{x}^{\mathrm{2}} }\:}{\:\sqrt{\mathrm{1}−{x}^{\mathrm{2}} }\:−{x}^{\mathrm{2}} }\right)\right\}+\frac{{x}+\mathrm{1}}{\left({x}+\mathrm{1}\right)^{\mathrm{2}} +\mathrm{4}} \\ $$$$\left(\mathrm{1}−{x}^{\mathrm{2}} \right)=\left(\mathrm{1}+{x}\right)\left(\mathrm{1}−{x}\right) \\ $$$$\mathrm{1}−{x}^{\mathrm{2}} =\mathrm{0}\:\:\:{at}\:{x}=\pm\mathrm{1} \\ $$$$\mathrm{1}−{x}^{\mathrm{2}} <\mathrm{0}\:\:{when}\:{x}>\mathrm{1} \\ $$$$\mathrm{1}−{x}^{\mathrm{2}} <\mathrm{0}\:{when}\:{x}<−\mathrm{1} \\ $$$$\mathrm{1}−{x}^{\mathrm{2}} >\mathrm{0}\:\:{when}\:{x}\:\left[−\mathrm{1},\mathrm{1}\right] \\ $$$$\mid{f}\left({x}\right)\mid_{{x}=−\mathrm{1}} \\ $$$$=\frac{\mathrm{1}}{\Pi}\left\{{tan}^{−} \left(\mathrm{1}\right)\right\}+\mathrm{0} \\ $$$$=\frac{\mathrm{1}}{\mathrm{4}} \\ $$$${f}\left({x}\right)\:{at}\:{x}=\mathrm{1} \\ $$$${f}\left({x}\right)=\frac{\mathrm{1}}{\Pi}\left\{{tan}^{−\mathrm{1}} \left(−\mathrm{1}\right)\right\}+\frac{\mathrm{2}}{\mathrm{8}} \\ $$$$=\frac{\mathrm{1}}{\Pi}×−\frac{\Pi}{\mathrm{4}}+\frac{\mathrm{1}}{\mathrm{4}} \\ $$$$=\mathrm{0} \\ $$$${range}\:{of}\:{f}\left({x}\right)\:\left[\mathrm{0},\frac{\mathrm{1}}{\mathrm{4}}\right] \\ $$$${pls}\:{check} \\ $$$${pls} \\ $$
