Question Number 101451 by yahyajan last updated on 02/Jul/20

Commented by Dwaipayan Shikari last updated on 02/Jul/20
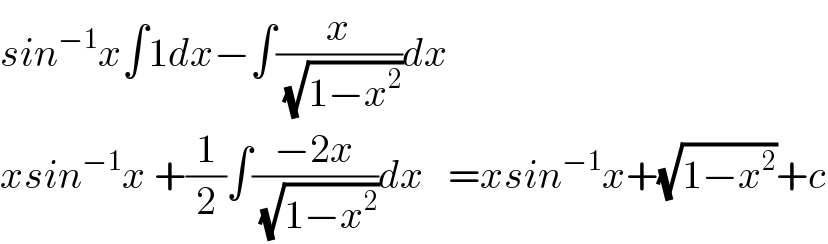
$${sin}^{−\mathrm{1}} {x}\int\mathrm{1}{dx}−\int\frac{{x}}{\:\sqrt{\mathrm{1}−{x}^{\mathrm{2}} }}{dx} \\ $$$${xsin}^{−\mathrm{1}} {x}\:+\frac{\mathrm{1}}{\mathrm{2}}\int\frac{−\mathrm{2}{x}}{\:\sqrt{\mathrm{1}−{x}^{\mathrm{2}} }}{dx}\:\:\:={xsin}^{−\mathrm{1}} {x}+\sqrt{\mathrm{1}−{x}^{\mathrm{2}} }+{c} \\ $$
Answered by floor(10²Eta[1]) last updated on 02/Jul/20
![∫f^(−1) (x)dx=xf^(−1) (x)−F○f^(−1) (x)+C let f^(−1) (x)=sin^(−1) (x)⇒f(x)=sin(x) ⇒F(x)=∫sin(x)dx=−cos(x) ∫sin^(−1) (x)dx=xsin^(−1) (x)+cos(sin^(−1) (x))+C cos(sin^(−1) (x))=cos(α) [sin^(−1) (x)=α⇒sin(α)=x] drawing a right triangle with angle α: sin(α)=x⇒((opp)/(hyp))=(x/1)⇒opp=x and hyp=1 ⇒adj=(√(1−x^2 ))⇒cos(α)=(√(1−x^2 )) ∫sin^(−1) (x)dx=xsin^(−1) (x)+(√(1−x^2 ))+C](https://www.tinkutara.com/question/Q101457.png)
$$\int{f}^{−\mathrm{1}} \left({x}\right){dx}={xf}^{−\mathrm{1}} \left({x}\right)−{F}\circ{f}^{−\mathrm{1}} \left({x}\right)+{C} \\ $$$${let}\:\:{f}^{−\mathrm{1}} \left({x}\right)={sin}^{−\mathrm{1}} \left({x}\right)\Rightarrow{f}\left({x}\right)={sin}\left({x}\right) \\ $$$$\Rightarrow{F}\left({x}\right)=\int{sin}\left({x}\right){dx}=−{cos}\left({x}\right) \\ $$$$\int{sin}^{−\mathrm{1}} \left({x}\right){dx}={xsin}^{−\mathrm{1}} \left({x}\right)+{cos}\left({sin}^{−\mathrm{1}} \left({x}\right)\right)+{C} \\ $$$${cos}\left({sin}^{−\mathrm{1}} \left({x}\right)\right)={cos}\left(\alpha\right)\:\left[{sin}^{−\mathrm{1}} \left({x}\right)=\alpha\Rightarrow{sin}\left(\alpha\right)={x}\right] \\ $$$${drawing}\:{a}\:{right}\:{triangle}\:{with}\:{angle}\:\alpha: \\ $$$${sin}\left(\alpha\right)={x}\Rightarrow\frac{{opp}}{{hyp}}=\frac{{x}}{\mathrm{1}}\Rightarrow{opp}={x}\:{and}\:{hyp}=\mathrm{1} \\ $$$$\Rightarrow{adj}=\sqrt{\mathrm{1}−{x}^{\mathrm{2}} }\Rightarrow{cos}\left(\alpha\right)=\sqrt{\mathrm{1}−{x}^{\mathrm{2}} } \\ $$$$\int{sin}^{−\mathrm{1}} \left({x}\right){dx}={xsin}^{−\mathrm{1}} \left({x}\right)+\sqrt{\mathrm{1}−{x}^{\mathrm{2}} }+{C} \\ $$
Answered by M±th+et+s last updated on 02/Jul/20
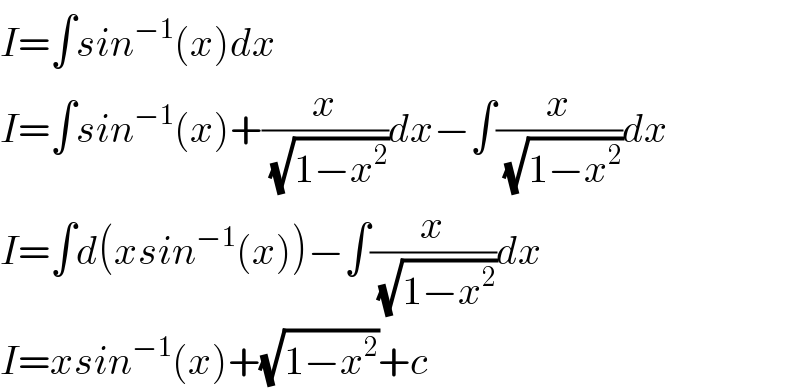
$${I}=\int{sin}^{−\mathrm{1}} \left({x}\right){dx} \\ $$$${I}=\int{sin}^{−\mathrm{1}} \left({x}\right)+\frac{{x}}{\:\sqrt{\mathrm{1}−{x}^{\mathrm{2}} }}{dx}−\int\frac{{x}}{\:\sqrt{\mathrm{1}−{x}^{\mathrm{2}} }}{dx} \\ $$$${I}=\int{d}\left({xsin}^{−\mathrm{1}} \left({x}\right)\right)−\int\frac{{x}}{\:\sqrt{\mathrm{1}−{x}^{\mathrm{2}} }}{dx} \\ $$$${I}={xsin}^{−\mathrm{1}} \left({x}\right)+\sqrt{\mathrm{1}−{x}^{\mathrm{2}} }+{c} \\ $$
