Question Number 167179 by mathocean1 last updated on 08/Mar/22
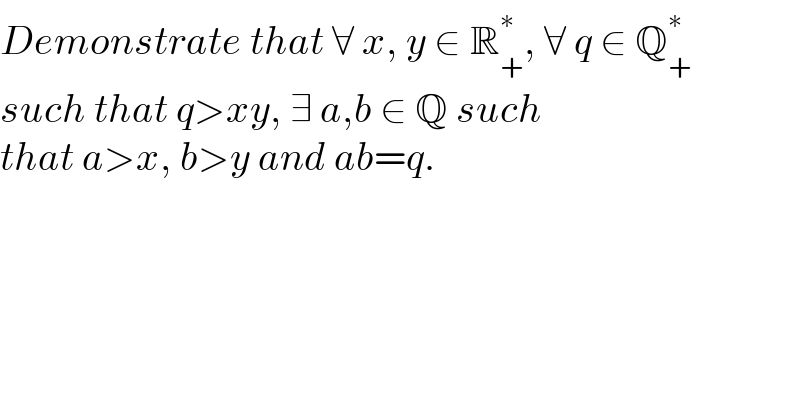
$${Demonstrate}\:{that}\:\forall\:{x},\:{y}\:\in\:\mathbb{R}_{+} ^{\ast} ,\:\forall\:{q}\:\in\:\mathbb{Q}_{+} ^{\ast} \\ $$$${such}\:{that}\:{q}>{xy},\:\exists\:{a},{b}\:\in\:\mathbb{Q}\:{such}\: \\ $$$${that}\:{a}>{x},\:{b}>{y}\:{and}\:{ab}={q}. \\ $$
Answered by mindispower last updated on 09/Mar/22
![suppose x<y let I=]x,(q/y)[≠{} ∴(q/y)>x⇔q>xy let a∈I∩Q≠{} (q/y)>a>x.....(1) y<(q/a)=b<x....(2) (1)&(2) Give us answer {} empty set](https://www.tinkutara.com/question/Q167193.png)
$${suppose}\:{x}<{y}\:\: \\ $$$$\left.{let}\:{I}=\right]{x},\frac{{q}}{{y}}\left[\neq\left\{\right\}\:\therefore\frac{{q}}{{y}}>{x}\Leftrightarrow{q}>{xy}\right. \\ $$$${let}\:{a}\in{I}\cap\mathbb{Q}\neq\left\{\right\}\:\frac{{q}}{{y}}>{a}>{x}…..\left(\mathrm{1}\right) \\ $$$${y}<\frac{{q}}{{a}}={b}<{x}….\left(\mathrm{2}\right) \\ $$$$\left(\mathrm{1}\right)\&\left(\mathrm{2}\right)\:{Give}\:{us}\:{answer} \\ $$$$\left\{\right\}\:{empty}\:{set}\: \\ $$$$ \\ $$$$ \\ $$$$ \\ $$$$ \\ $$
