Question Number 167421 by infinityaction last updated on 16/Mar/22

Answered by mindispower last updated on 16/Mar/22
![cot^2 (((kπ)/(2n+1)))=cot^2 (sπ)=(i((e^(is) +e^(−is) )/(e^(is) −e^(−is) )))^2 = ⇒−cot^2 (sπ)=(((e^(2ia) +1)/(e^(2ia) −1)))^2 ⇒icot(sπ)p=((e^(2is) +1)/(e^(2is) −1)) ⇒e^(2is) =((1+ia)/(ia−1)),((e^(2is) )^(2n+1) −1)=0 ⇒(1+ia)^(2n+1) +(1−ia)^(2n+1) =0 ⇒Σ_(k=0) ^(2n+1) (((2n+1)),(( k)) )((ia)^k +(−ia)^k )=0 ⇒Σ_(k=0) ^n (((2n+1)),(( 2k)) ).2(−1)^k a^(2k) =0 a^2 =tg^2 (((sπ)/(2n+1))),for som s∈[1,n] ⇒tg^2 (((sπ)/(2n+1))) Root Of 2Σ_(k=0) ^n (((2n+1)),(( 2k)) )(−1)^k X^k =0 (−1)^n (((2n+1)),(( 1)) )X^n +Σ_(k=0) ^(n−1) (−1)^k (((2n+1)),(( k)) )X^k =0 ⇔X^n +Σ_(k=0) ^(n−1) (((−1)^(k−n) (((2n+1)),(( k)) ))/ (((2n+1)),(( 1)) ))X^k =0](https://www.tinkutara.com/question/Q167429.png)
$${cot}^{\mathrm{2}} \left(\frac{{k}\pi}{\mathrm{2}{n}+\mathrm{1}}\right)={cot}^{\mathrm{2}} \left({s}\pi\right)=\left({i}\frac{{e}^{{is}} +{e}^{−{is}} }{{e}^{{is}} −{e}^{−{is}} }\right)^{\mathrm{2}} = \\ $$$$\Rightarrow−{cot}^{\mathrm{2}} \left({s}\pi\right)=\left(\frac{{e}^{\mathrm{2}{ia}} +\mathrm{1}}{{e}^{\mathrm{2}{ia}} −\mathrm{1}}\overset{\mathrm{2}} {\right)} \\ $$$$\Rightarrow{icot}\left({s}\pi\right){p}=\frac{{e}^{\mathrm{2}{is}} +\mathrm{1}}{{e}^{\mathrm{2}{is}} −\mathrm{1}} \\ $$$$\Rightarrow{e}^{\mathrm{2}{is}} =\frac{\mathrm{1}+{ia}}{{ia}−\mathrm{1}},\left(\left({e}^{\mathrm{2}{is}} \right)^{\mathrm{2}{n}+\mathrm{1}} −\mathrm{1}\right)=\mathrm{0} \\ $$$$\Rightarrow\left(\mathrm{1}+\boldsymbol{{ia}}\right)^{\mathrm{2}\boldsymbol{{n}}+\mathrm{1}} +\left(\mathrm{1}−\boldsymbol{{ia}}\right)^{\mathrm{2}\boldsymbol{{n}}+\mathrm{1}} =\mathrm{0} \\ $$$$\Rightarrow\underset{{k}=\mathrm{0}} {\overset{\mathrm{2}{n}+\mathrm{1}} {\sum}}\begin{pmatrix}{\mathrm{2}{n}+\mathrm{1}}\\{\:\:\:\:{k}}\end{pmatrix}\left(\left({ia}\right)^{{k}} +\left(−{ia}\right)^{{k}} \right)=\mathrm{0} \\ $$$$\Rightarrow\underset{{k}=\mathrm{0}} {\overset{{n}} {\sum}}\begin{pmatrix}{\mathrm{2}{n}+\mathrm{1}}\\{\:\:\:\:\mathrm{2}{k}}\end{pmatrix}.\mathrm{2}\left(−\mathrm{1}\right)^{{k}} {a}^{\mathrm{2}{k}} =\mathrm{0} \\ $$$${a}^{\mathrm{2}} ={tg}^{\mathrm{2}} \left(\frac{{s}\pi}{\mathrm{2}{n}+\mathrm{1}}\right),{for}\:{som}\:{s}\in\left[\mathrm{1},{n}\right] \\ $$$$\Rightarrow{tg}^{\mathrm{2}} \left(\frac{{s}\pi}{\mathrm{2}{n}+\mathrm{1}}\right)\:{Root}\:{Of} \\ $$$$\mathrm{2}\underset{{k}=\mathrm{0}} {\overset{{n}} {\sum}}\begin{pmatrix}{\mathrm{2}{n}+\mathrm{1}}\\{\:\:\:\mathrm{2}{k}}\end{pmatrix}\left(−\mathrm{1}\right)^{{k}} {X}^{{k}} =\mathrm{0} \\ $$$$\left(−\mathrm{1}\right)^{{n}} \begin{pmatrix}{\mathrm{2}{n}+\mathrm{1}}\\{\:\:\:\:\mathrm{1}}\end{pmatrix}{X}^{{n}} +\underset{{k}=\mathrm{0}} {\overset{{n}−\mathrm{1}} {\sum}}\left(−\mathrm{1}\right)^{{k}} \begin{pmatrix}{\mathrm{2}{n}+\mathrm{1}}\\{\:\:\:\:\:{k}}\end{pmatrix}{X}^{{k}} =\mathrm{0} \\ $$$$\Leftrightarrow{X}^{{n}} +\underset{{k}=\mathrm{0}} {\overset{{n}−\mathrm{1}} {\sum}}\frac{\left(−\mathrm{1}\right)^{{k}−{n}} \begin{pmatrix}{\mathrm{2}{n}+\mathrm{1}}\\{\:\:\:{k}}\end{pmatrix}}{\begin{pmatrix}{\mathrm{2}{n}+\mathrm{1}}\\{\:\:\:\:\:\:\mathrm{1}}\end{pmatrix}}{X}^{{k}} =\mathrm{0} \\ $$$$ \\ $$$$ \\ $$
Commented by infinityaction last updated on 16/Mar/22

$${thank}\:{you}\:{sir} \\ $$
Commented by infinityaction last updated on 16/Mar/22
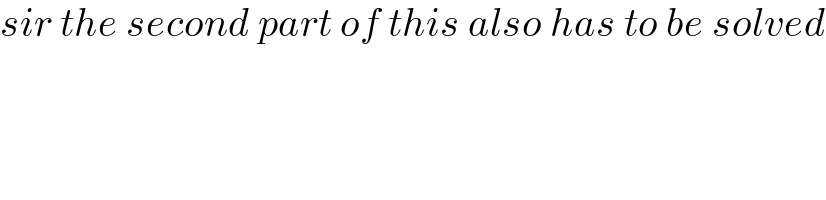
$${sir}\:{the}\:{second}\:{part}\:{of}\:{this}\:{also}\:{has}\:{to}\:{be}\:{solved} \\ $$
