Question Number 167700 by HongKing last updated on 23/Mar/22
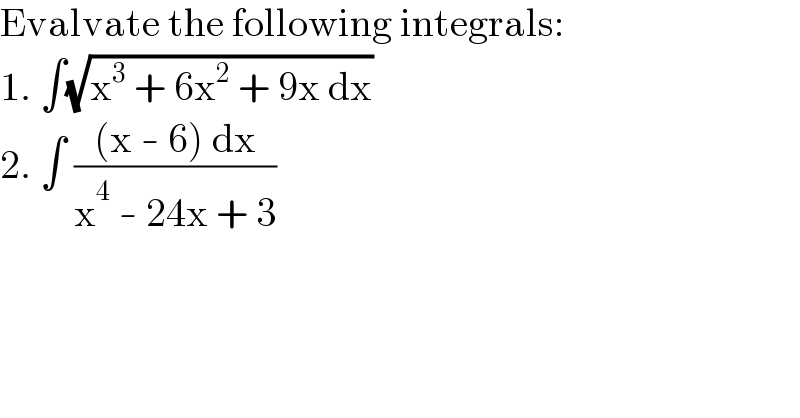
$$\mathrm{Evalvate}\:\mathrm{the}\:\mathrm{following}\:\mathrm{integrals}: \\ $$$$\mathrm{1}.\:\int\sqrt{\mathrm{x}^{\mathrm{3}} \:+\:\mathrm{6x}^{\mathrm{2}} \:+\:\mathrm{9x}\:\mathrm{dx}} \\ $$$$\mathrm{2}.\:\int\:\frac{\left(\mathrm{x}\:-\:\mathrm{6}\right)\:\mathrm{dx}}{\mathrm{x}^{\mathrm{4}} \:-\:\mathrm{24x}\:+\:\mathrm{3}} \\ $$
Answered by MJS_new last updated on 23/Mar/22
![∫(√(x^3 +6x^2 +9x))dx=∫∣x+3∣(√x)dx= [defined for x≥0] =∫(x^(3/2) +3x^(1/2) )dx= =(2/5)x^(5/2) +2x^(3/2) +C](https://www.tinkutara.com/question/Q167710.png)
$$\int\sqrt{{x}^{\mathrm{3}} +\mathrm{6}{x}^{\mathrm{2}} +\mathrm{9}{x}}{dx}=\int\mid{x}+\mathrm{3}\mid\sqrt{{x}}{dx}= \\ $$$$\:\:\:\:\:\left[\mathrm{defined}\:\mathrm{for}\:{x}\geqslant\mathrm{0}\right] \\ $$$$=\int\left({x}^{\mathrm{3}/\mathrm{2}} +\mathrm{3}{x}^{\mathrm{1}/\mathrm{2}} \right){dx}= \\ $$$$=\frac{\mathrm{2}}{\mathrm{5}}{x}^{\mathrm{5}/\mathrm{2}} +\mathrm{2}{x}^{\mathrm{3}/\mathrm{2}} +{C} \\ $$
