Question Number 102642 by otchereabdullai@gmail.com last updated on 10/Jul/20

Answered by som(math1967) last updated on 10/Jul/20
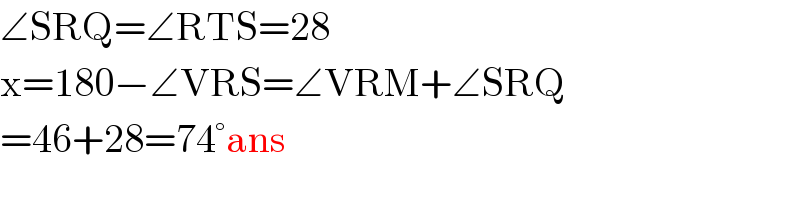
$$\angle\mathrm{SRQ}=\angle\mathrm{RTS}=\mathrm{28} \\ $$$$\mathrm{x}=\mathrm{180}−\angle\mathrm{VRS}=\angle\mathrm{VRM}+\angle\mathrm{SRQ} \\ $$$$=\mathrm{46}+\mathrm{28}=\mathrm{74}°\mathrm{ans} \\ $$
Commented by bemath last updated on 10/Jul/20
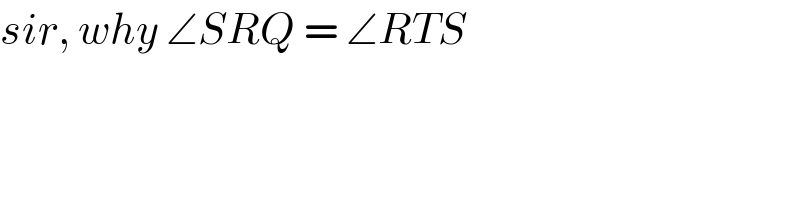
$${sir},\:{why}\:\angle{SRQ}\:=\:\angle{RTS} \\ $$
Commented by som(math1967) last updated on 10/Jul/20
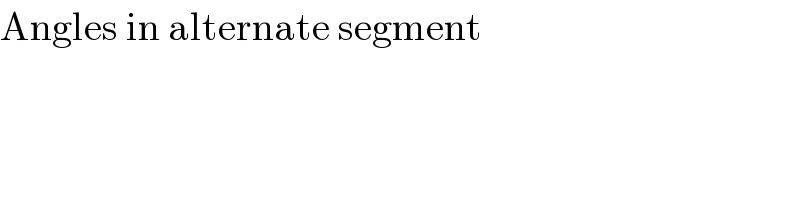
$$\mathrm{Angles}\:\mathrm{in}\:\mathrm{alternate}\:\mathrm{segment} \\ $$
Commented by som(math1967) last updated on 10/Jul/20
![let O is centre ∴∠ORS=∠OSR [OR=OS] ∠ORS=90−(1/2)∠ROS ∠ORS=90−∠RTS ∴∠RTS=90−∠ORS Again ∠SRQ=90−∠ORS [∵OR radd. RQ tanjent] ∴∠RTS=∠SRQ](https://www.tinkutara.com/question/Q102676.png)
$$\mathrm{let}\:\mathrm{O}\:\mathrm{is}\:\mathrm{centre} \\ $$$$\therefore\angle\mathrm{ORS}=\angle\mathrm{OSR}\:\left[\mathrm{OR}=\mathrm{OS}\right] \\ $$$$\angle\mathrm{ORS}=\mathrm{90}−\frac{\mathrm{1}}{\mathrm{2}}\angle\mathrm{ROS} \\ $$$$\angle\mathrm{ORS}=\mathrm{90}−\angle\mathrm{RTS} \\ $$$$\therefore\angle\mathrm{RTS}=\mathrm{90}−\angle\mathrm{ORS} \\ $$$$\mathrm{Again}\:\angle\mathrm{SRQ}=\mathrm{90}−\angle\mathrm{ORS} \\ $$$$\left[\because\mathrm{OR}\:\mathrm{radd}.\:\mathrm{RQ}\:\mathrm{tanjent}\right] \\ $$$$\therefore\angle\mathrm{RTS}=\angle\mathrm{SRQ} \\ $$$$ \\ $$
Commented by som(math1967) last updated on 10/Jul/20

Commented by otchereabdullai@gmail.com last updated on 10/Jul/20
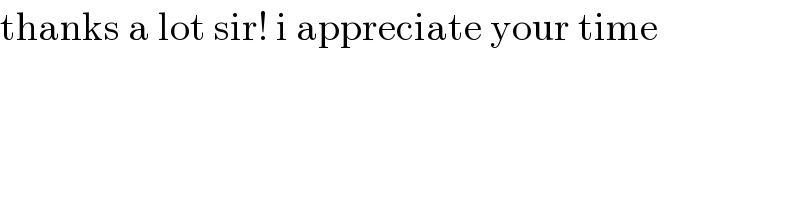
$$\mathrm{thanks}\:\mathrm{a}\:\mathrm{lot}\:\mathrm{sir}!\:\mathrm{i}\:\mathrm{appreciate}\:\mathrm{your}\:\mathrm{time} \\ $$
Answered by bramlex last updated on 10/Jul/20
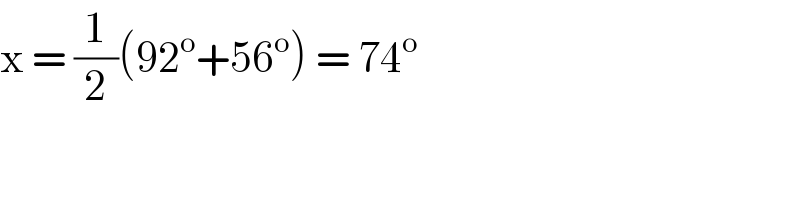
$$\mathrm{x}\:=\:\frac{\mathrm{1}}{\mathrm{2}}\left(\mathrm{92}^{\mathrm{o}} +\mathrm{56}^{\mathrm{o}} \right)\:=\:\mathrm{74}^{\mathrm{o}} \\ $$
Commented by bramlex last updated on 10/Jul/20

Commented by otchereabdullai@gmail.com last updated on 10/Jul/20

$$\mathrm{wow}\:! \\ $$
