Question Number 102840 by Dwaipayan Shikari last updated on 11/Jul/20
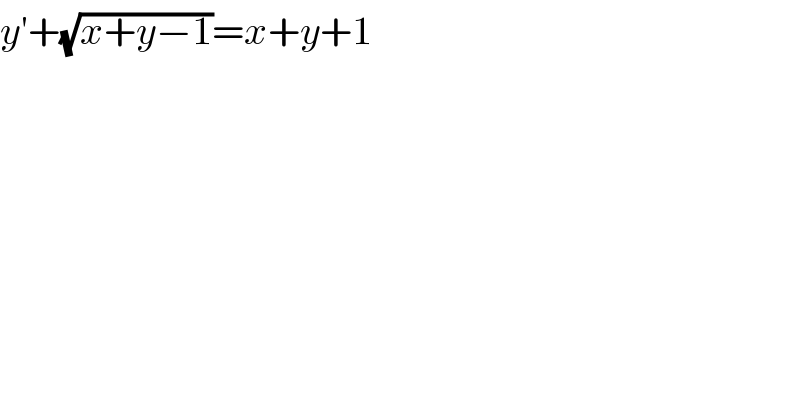
$${y}'+\sqrt{{x}+{y}−\mathrm{1}}={x}+{y}+\mathrm{1} \\ $$
Answered by OlafThorendsen last updated on 12/Jul/20
![y = Y^2 −x+1 2Y′Y−1+(√Y^2 ) = Y^2 +2 2Y′Y−1+Y = Y^2 +2 2Y′Y = Y^2 −Y+3 Y′((2Y)/(Y^2 −Y+3)) = 1 Y′[((2Y−1)/(Y^2 −Y+3))+(1/(Y^2 −Y+3))] = 1 Y′[((2Y−1)/(Y^2 −Y+3))+(1/((Y−(1/2))^2 +((11)/4)))] = 1 Y′[((2Y−1)/(Y^2 −Y+3))+((4/(11))/((4/(11))(Y−(1/2))^2 +1))] = 1 ln(Y^2 −Y+3)+(2/( (√(11))))arctan(2/( (√(11))))(Y−(1/2)) = x+C](https://www.tinkutara.com/question/Q102982.png)
$${y}\:=\:\mathrm{Y}^{\mathrm{2}} −{x}+\mathrm{1} \\ $$$$\mathrm{2Y}'\mathrm{Y}−\mathrm{1}+\sqrt{\mathrm{Y}^{\mathrm{2}} }\:=\:\mathrm{Y}^{\mathrm{2}} +\mathrm{2} \\ $$$$\mathrm{2Y}'\mathrm{Y}−\mathrm{1}+\mathrm{Y}\:=\:\mathrm{Y}^{\mathrm{2}} +\mathrm{2} \\ $$$$\mathrm{2Y}'\mathrm{Y}\:=\:\mathrm{Y}^{\mathrm{2}} −\mathrm{Y}+\mathrm{3} \\ $$$$\mathrm{Y}'\frac{\mathrm{2Y}}{\mathrm{Y}^{\mathrm{2}} −\mathrm{Y}+\mathrm{3}}\:=\:\mathrm{1} \\ $$$$\mathrm{Y}'\left[\frac{\mathrm{2Y}−\mathrm{1}}{\mathrm{Y}^{\mathrm{2}} −\mathrm{Y}+\mathrm{3}}+\frac{\mathrm{1}}{\mathrm{Y}^{\mathrm{2}} −\mathrm{Y}+\mathrm{3}}\right]\:=\:\mathrm{1} \\ $$$$\mathrm{Y}'\left[\frac{\mathrm{2Y}−\mathrm{1}}{\mathrm{Y}^{\mathrm{2}} −\mathrm{Y}+\mathrm{3}}+\frac{\mathrm{1}}{\left(\mathrm{Y}−\frac{\mathrm{1}}{\mathrm{2}}\right)^{\mathrm{2}} +\frac{\mathrm{11}}{\mathrm{4}}}\right]\:=\:\mathrm{1} \\ $$$$\mathrm{Y}'\left[\frac{\mathrm{2Y}−\mathrm{1}}{\mathrm{Y}^{\mathrm{2}} −\mathrm{Y}+\mathrm{3}}+\frac{\frac{\mathrm{4}}{\mathrm{11}}}{\frac{\mathrm{4}}{\mathrm{11}}\left(\mathrm{Y}−\frac{\mathrm{1}}{\mathrm{2}}\right)^{\mathrm{2}} +\mathrm{1}}\right]\:=\:\mathrm{1} \\ $$$$\mathrm{ln}\left(\mathrm{Y}^{\mathrm{2}} −\mathrm{Y}+\mathrm{3}\right)+\frac{\mathrm{2}}{\:\sqrt{\mathrm{11}}}\mathrm{arctan}\frac{\mathrm{2}}{\:\sqrt{\mathrm{11}}}\left(\mathrm{Y}−\frac{\mathrm{1}}{\mathrm{2}}\right)\:=\:{x}+\mathrm{C} \\ $$$$ \\ $$
