Question Number 37730 by Rio Mike last updated on 17/Jun/18

$$\:{Differentiate}\: \\ $$$${x}\left(\mathrm{1}+{x}\right)^{\mathrm{4}} \: \\ $$$$ \\ $$
Commented by Rio Mike last updated on 17/Jun/18
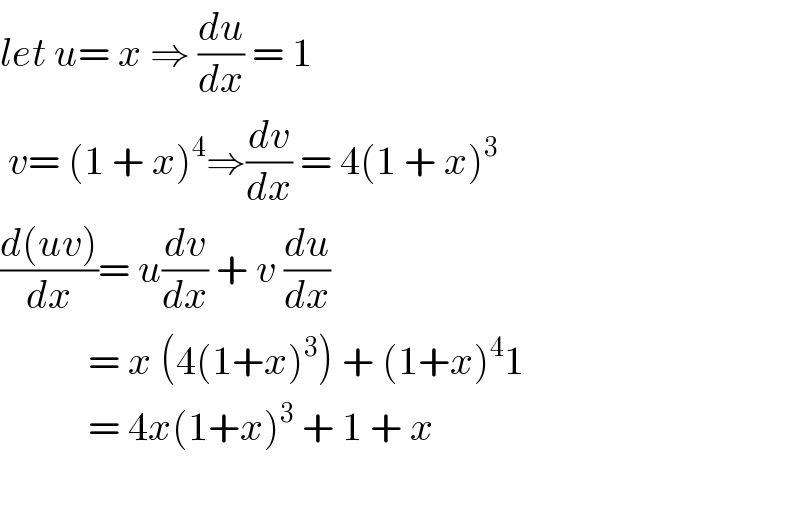
$${let}\:{u}=\:{x}\:\Rightarrow\:\frac{{du}}{{dx}}\:=\:\mathrm{1} \\ $$$$\:{v}=\:\left(\mathrm{1}\:+\:{x}\right)^{\mathrm{4}} \Rightarrow\frac{{dv}}{{dx}}\:=\:\mathrm{4}\left(\mathrm{1}\:+\:{x}\right)^{\mathrm{3}} \\ $$$$\frac{{d}\left({uv}\right)}{{dx}}=\:{u}\frac{{dv}}{{dx}}\:+\:{v}\:\frac{{du}}{{dx}} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:=\:{x}\:\left(\mathrm{4}\left(\mathrm{1}+{x}\right)^{\mathrm{3}} \right)\:+\:\left(\mathrm{1}+{x}\right)^{\mathrm{4}} \mathrm{1} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:=\:\mathrm{4}{x}\left(\mathrm{1}+{x}\right)^{\mathrm{3}} \:+\:\mathrm{1}\:+\:{x} \\ $$$$ \\ $$
Answered by MJS last updated on 17/Jun/18
![(uv)′=u′v+uv′ (d/dx)[x(x+1)^4 ]=(x+1)^4 +4(x+1)^3 =(x+5)(x+1)^3](https://www.tinkutara.com/question/Q37756.png)
$$\left({uv}\right)'={u}'{v}+{uv}' \\ $$$$\frac{{d}}{{dx}}\left[{x}\left({x}+\mathrm{1}\right)^{\mathrm{4}} \right]=\left({x}+\mathrm{1}\right)^{\mathrm{4}} +\mathrm{4}\left({x}+\mathrm{1}\right)^{\mathrm{3}} =\left({x}+\mathrm{5}\right)\left({x}+\mathrm{1}\right)^{\mathrm{3}} \\ $$
