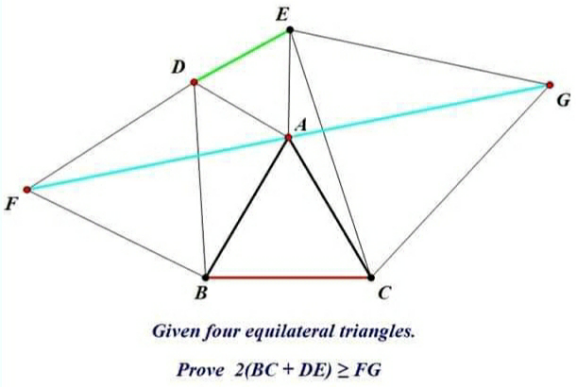
Question Number 168921 by Shrinava last updated on 21/Apr/22
Answered by mr W last updated on 22/Apr/22
Commented by Tawa11 last updated on 22/Apr/22

$$\mathrm{Great}\:\mathrm{sir}. \\ $$
Commented by mr W last updated on 22/Apr/22
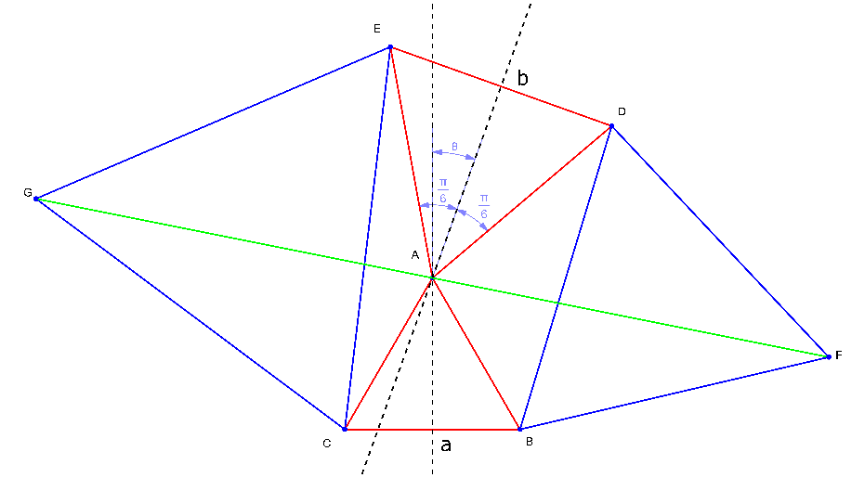
![say BC=a, DE=b let BD=c c^2 =a^2 +b^2 −2ab cos (π−θ−(π/3)) c^2 =a^2 +b^2 +ab(cos θ−(√3) sin θ) ((sin ∠ABD)/(AD))=((sin (θ+(π/3)))/(BD)) ⇒sin ∠ABD=((b sin (θ+(π/3)))/c) cos ∠ABD=((a^2 +c^2 −b^2 )/(2ac)) AF^2 =a^2 +c^2 −2ac cos (∠ABD+(π/3)) AF^2 =a^2 +c^2 −ac (cos ∠ABD−(√3) sin ∠ABD) AF^2 =a^2 +c^2 −ac cos ∠ABD+(√3) ab sin (θ+(π/3))] AF^2 =a^2 +c^2 −ac×((a^2 +c^2 −b^2 )/(2ac))+(√3) ab sin (θ+(π/3))] AF^2 =((a^2 +b^2 +c^2 )/2)+(√3) ab sin (θ+(π/3)) AF^2 =((a^2 +b^2 +a^2 +b^2 +ab(cos θ−(√3) sin θ))/2)+((√3)/2)ab (sin θ+(√3) cos θ) AF^2 =a^2 +b^2 +2ab cos θ AF=(√(a^2 +b^2 +2ab cos θ)) replace θ with −θ we get AG=(√(a^2 +b^2 +2ab cos (−θ))) AG=(√(a^2 +b^2 +2ab cos θ)) i.e. AF=AG it can also be shown that F,A,G are collinear. FG=AF+AG=2(√(a^2 +b^2 +2ab cos θ)) ≤2(√(a^2 +b^2 +2ab))=2(a+b) i.e. 2(BC+DE)≥FG](https://www.tinkutara.com/question/Q168958.png)
$${say}\:{BC}={a},\:{DE}={b} \\ $$$${let}\:{BD}={c} \\ $$$${c}^{\mathrm{2}} ={a}^{\mathrm{2}} +{b}^{\mathrm{2}} −\mathrm{2}{ab}\:\mathrm{cos}\:\left(\pi−\theta−\frac{\pi}{\mathrm{3}}\right) \\ $$$${c}^{\mathrm{2}} ={a}^{\mathrm{2}} +{b}^{\mathrm{2}} +{ab}\left(\mathrm{cos}\:\theta−\sqrt{\mathrm{3}}\:\mathrm{sin}\:\theta\right) \\ $$$$\frac{\mathrm{sin}\:\angle{ABD}}{{AD}}=\frac{\mathrm{sin}\:\left(\theta+\frac{\pi}{\mathrm{3}}\right)}{{BD}} \\ $$$$\Rightarrow\mathrm{sin}\:\angle{ABD}=\frac{{b}\:\mathrm{sin}\:\left(\theta+\frac{\pi}{\mathrm{3}}\right)}{{c}} \\ $$$$\mathrm{cos}\:\angle{ABD}=\frac{{a}^{\mathrm{2}} +{c}^{\mathrm{2}} −{b}^{\mathrm{2}} }{\mathrm{2}{ac}} \\ $$$$ \\ $$$${AF}^{\mathrm{2}} ={a}^{\mathrm{2}} +{c}^{\mathrm{2}} −\mathrm{2}{ac}\:\mathrm{cos}\:\left(\angle{ABD}+\frac{\pi}{\mathrm{3}}\right) \\ $$$${AF}^{\mathrm{2}} ={a}^{\mathrm{2}} +{c}^{\mathrm{2}} −{ac}\:\left(\mathrm{cos}\:\angle{ABD}−\sqrt{\mathrm{3}}\:\mathrm{sin}\:\angle{ABD}\right) \\ $$$$\left.{AF}^{\mathrm{2}} ={a}^{\mathrm{2}} +{c}^{\mathrm{2}} −{ac}\:\mathrm{cos}\:\angle{ABD}+\sqrt{\mathrm{3}}\:{ab}\:\mathrm{sin}\:\left(\theta+\frac{\pi}{\mathrm{3}}\right)\right] \\ $$$$\left.{AF}^{\mathrm{2}} ={a}^{\mathrm{2}} +{c}^{\mathrm{2}} −{ac}×\frac{{a}^{\mathrm{2}} +{c}^{\mathrm{2}} −{b}^{\mathrm{2}} }{\mathrm{2}{ac}}+\sqrt{\mathrm{3}}\:{ab}\:\mathrm{sin}\:\left(\theta+\frac{\pi}{\mathrm{3}}\right)\right] \\ $$$${AF}^{\mathrm{2}} =\frac{{a}^{\mathrm{2}} +{b}^{\mathrm{2}} +{c}^{\mathrm{2}} }{\mathrm{2}}+\sqrt{\mathrm{3}}\:{ab}\:\mathrm{sin}\:\left(\theta+\frac{\pi}{\mathrm{3}}\right) \\ $$$${AF}^{\mathrm{2}} =\frac{{a}^{\mathrm{2}} +{b}^{\mathrm{2}} +{a}^{\mathrm{2}} +{b}^{\mathrm{2}} +{ab}\left(\mathrm{cos}\:\theta−\sqrt{\mathrm{3}}\:\mathrm{sin}\:\theta\right)}{\mathrm{2}}+\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}{ab}\:\left(\mathrm{sin}\:\theta+\sqrt{\mathrm{3}}\:\mathrm{cos}\:\theta\right) \\ $$$${AF}^{\mathrm{2}} ={a}^{\mathrm{2}} +{b}^{\mathrm{2}} +\mathrm{2}{ab}\:\mathrm{cos}\:\theta \\ $$$${AF}=\sqrt{{a}^{\mathrm{2}} +{b}^{\mathrm{2}} +\mathrm{2}{ab}\:\mathrm{cos}\:\theta} \\ $$$${replace}\:\theta\:{with}\:−\theta\:{we}\:{get} \\ $$$${AG}=\sqrt{{a}^{\mathrm{2}} +{b}^{\mathrm{2}} +\mathrm{2}{ab}\:\mathrm{cos}\:\left(−\theta\right)} \\ $$$${AG}=\sqrt{{a}^{\mathrm{2}} +{b}^{\mathrm{2}} +\mathrm{2}{ab}\:\mathrm{cos}\:\theta} \\ $$$${i}.{e}.\:{AF}={AG} \\ $$$${it}\:{can}\:{also}\:{be}\:{shown}\:{that}\:{F},{A},{G} \\ $$$${are}\:{collinear}. \\ $$$${FG}={AF}+{AG}=\mathrm{2}\sqrt{{a}^{\mathrm{2}} +{b}^{\mathrm{2}} +\mathrm{2}{ab}\:\mathrm{cos}\:\theta} \\ $$$$\:\:\:\:\:\:\:\leqslant\mathrm{2}\sqrt{{a}^{\mathrm{2}} +{b}^{\mathrm{2}} +\mathrm{2}{ab}}=\mathrm{2}\left({a}+{b}\right) \\ $$$${i}.{e}.\:\mathrm{2}\left({BC}+{DE}\right)\geqslant{FG} \\ $$
Commented by Shrinava last updated on 23/Apr/22

$$\mathrm{Cool}\:\mathrm{dear}\:\mathrm{sir} \\ $$
