Menu Close

Question-169211

Tinku Tara 0 Comments
Pin




Question Number 169211 by 0731619 last updated on 26/Apr/22
Commented by infinityaction last updated on 26/Apr/22
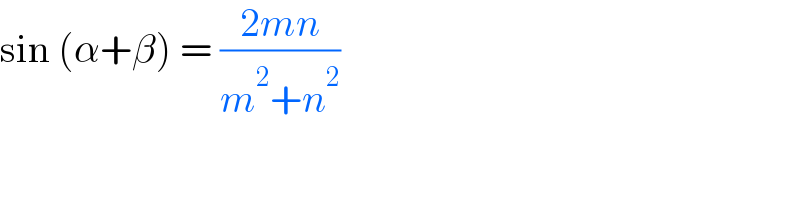
sin (α+β) = ((2mn)/(m^2 +n^2 ))
$$\mathrm{sin}\:\left(\alpha+\beta\right)\:=\:\frac{\mathrm{2}{mn}}{{m}^{\mathrm{2}} +{n}^{\mathrm{2}} } \\ $$
Commented by 0731619 last updated on 26/Apr/22
solution plz
$${solution}\:{plz} \\ $$
Commented by infinityaction last updated on 26/Apr/22
sin^2 𝛂 + sin^2 𝛃 + 2sin (𝛂)sin (𝛃) =n^2 ..(1) cos^2 𝛂 +cos^2 𝛃 + 2cos (𝛂)cos (𝛃) = m^2 ....(2) eq^n .(1) + eq^n . (2) 2 + 2(sin 𝛂 sin 𝛃 + cos 𝛂 cos 𝛃) = n^2 +m^2 ...(3) 2{1 + cos (𝛂−𝛃)} = m^2 + n^(2 ) .....(4) eq^n .(1) × eq^n .(2) (sin α +sin β)(cos α+cos β) = mn cos αsin α + cos βsin β +cosα sinβ + cosβ sinα = mn sin 2α +sin 2β + 2sin (𝛂+𝛃) = 2mn 2sin (𝛂+𝛃)∙cos (𝛂−𝛃) + 2sin (𝛂+𝛃) = 2mn 2sin (α+β){cos (𝛂−𝛃) + 1} = 2mn ....(5) ((eq^n .(5))/(eq^n .(4))) ((2sin (𝛂+𝛃){cos(𝛂−𝛃) + 1} )/(2{1+cos (𝛂−𝛃)})) = ((2mn)/(m^2 +n^2 )) sin (𝛂+𝛃) = ((2mn)/(m^2 +n^2 ))
$$\:\:\:\boldsymbol{\mathrm{sin}}\:^{\mathrm{2}} \boldsymbol{\alpha}\:+\:\boldsymbol{\mathrm{sin}}^{\mathrm{2}} \:\boldsymbol{\beta}\:+\:\mathrm{2}\boldsymbol{\mathrm{sin}}\:\left(\boldsymbol{\alpha}\right)\boldsymbol{\mathrm{sin}}\:\left(\boldsymbol{\beta}\right)\:=\boldsymbol{{n}}^{\mathrm{2}} \:..\left(\mathrm{1}\right) \\ $$$$\:\:\:\boldsymbol{\mathrm{cos}}\:^{\mathrm{2}} \boldsymbol{\alpha}\:+\boldsymbol{\mathrm{cos}}\:^{\mathrm{2}} \boldsymbol{\beta}\:+\:\mathrm{2}\boldsymbol{\mathrm{cos}}\:\left(\boldsymbol{\alpha}\right)\boldsymbol{\mathrm{cos}}\:\left(\boldsymbol{\beta}\right)\:=\:\boldsymbol{{m}}^{\mathrm{2}} \:….\left(\mathrm{2}\right) \\ $$$$\:\:\:\:{eq}^{{n}} .\left(\mathrm{1}\right)\:+\:{eq}^{{n}} .\:\left(\mathrm{2}\right) \\ $$$$\:\:\:\mathrm{2}\:+\:\mathrm{2}\left(\boldsymbol{\mathrm{sin}}\:\boldsymbol{\alpha}\:\boldsymbol{\mathrm{sin}}\:\boldsymbol{\beta}\:+\:\boldsymbol{\mathrm{cos}}\:\boldsymbol{\alpha}\:\boldsymbol{\mathrm{cos}}\:\boldsymbol{\beta}\right)\:=\:{n}^{\mathrm{2}} +{m}^{\mathrm{2}} \:…\left(\mathrm{3}\right) \\ $$$$\:\:\:\mathrm{2}\left\{\mathrm{1}\:+\:\mathrm{cos}\:\left(\boldsymbol{\alpha}−\boldsymbol{\beta}\right)\right\}\:=\:{m}^{\mathrm{2}} \:+\:{n}^{\mathrm{2}\:} \:\:…..\left(\mathrm{4}\right) \\ $$$$\:\:\:{eq}^{{n}} .\left(\mathrm{1}\right)\:×\:{eq}^{{n}} .\left(\mathrm{2}\right) \\ $$$$\:\:\left(\mathrm{sin}\:\alpha\:+\mathrm{sin}\:\beta\right)\left(\mathrm{cos}\:\alpha+\mathrm{cos}\:\beta\right)\:=\:{mn} \\ $$$$\mathrm{cos}\:\alpha\mathrm{sin}\:\alpha\:+\:\mathrm{cos}\:\beta\mathrm{sin}\:\beta\:+\mathrm{cos}\alpha\:\mathrm{sin}\beta\:\:+\:\mathrm{cos}\beta\:\mathrm{sin}\alpha\:=\:{mn} \\ $$$$\:\:\mathrm{sin}\:\mathrm{2}\alpha\:+\mathrm{sin}\:\mathrm{2}\beta\:+\:\mathrm{2sin}\:\left(\boldsymbol{\alpha}+\boldsymbol{\beta}\right)\:=\:\mathrm{2}{mn}\: \\ $$$$\:\:\mathrm{2sin}\:\left(\boldsymbol{\alpha}+\boldsymbol{\beta}\right)\centerdot\mathrm{cos}\:\left(\boldsymbol{\alpha}−\boldsymbol{\beta}\right)\:+\:\mathrm{2sin}\:\left(\boldsymbol{\alpha}+\boldsymbol{\beta}\right)\:=\:\mathrm{2}{mn} \\ $$$$\:\:\mathrm{2sin}\:\left(\alpha+\beta\right)\left\{\mathrm{cos}\:\left(\boldsymbol{\alpha}−\boldsymbol{\beta}\right)\:+\:\mathrm{1}\right\}\:=\:\mathrm{2}{mn}\:\:\:….\left(\mathrm{5}\right) \\ $$$$\:\:\:\:\:\frac{{eq}^{{n}} .\left(\mathrm{5}\right)}{{eq}^{{n}} .\left(\mathrm{4}\right)} \\ $$$$\:\:\:\frac{\mathrm{2sin}\:\left(\boldsymbol{\alpha}+\boldsymbol{\beta}\right)\left\{\mathrm{cos}\left(\boldsymbol{\alpha}−\boldsymbol{\beta}\right)\:+\:\mathrm{1}\right\}\:}{\mathrm{2}\left\{\mathrm{1}+\mathrm{cos}\:\left(\boldsymbol{\alpha}−\boldsymbol{\beta}\right)\right\}}\:=\:\frac{\mathrm{2}{mn}}{{m}^{\mathrm{2}} +{n}^{\mathrm{2}} } \\ $$$$\:\:\:\mathrm{sin}\:\left(\boldsymbol{\alpha}+\boldsymbol{\beta}\right)\:\:\:=\:\:\frac{\mathrm{2}\boldsymbol{{mn}}}{\boldsymbol{{m}}^{\mathrm{2}} +\boldsymbol{{n}}^{\mathrm{2}} } \\ $$$$\: \\ $$$$\:\:\: \\ $$
Commented by som(math1967) last updated on 26/Apr/22
sinα+sinβ=m ⇒2sin(((α+β)/2))cos(((α−β)/2))=m ....i) cosα+cosβ=m 2cos(((α+β)/2))cos(((α−β)/2))=n ....ii) i) ×ii 2sin(((α+β)/2))cos(((α+β)/2))2cos^2 (((α−β)/2))=mn ⇒sin(α+β)=((mn)/(2cos^2 (((α−β)/2)))) (i)^2 +(ii)^2 4cos^2 (((α−β)/2))[sin^2 (((α+β)/2))+cos^2 (((α+β)/2))] =m^2 +n^2 ∴2cos^2 (((α−β)/2))=((m^2 +n^2 )/2) ∴sin(α+β)=((mn)/(2cos^2 (((α−β)/2)))) =((mn)/((m^2 +n^2 )/2)) ∴sin(𝛂+𝛃)=((2mn)/(m^2 +n^2 ))
$${sin}\alpha+{sin}\beta={m} \\ $$$$\left.\Rightarrow\mathrm{2}{sin}\left(\frac{\alpha+\beta}{\mathrm{2}}\right){cos}\left(\frac{\alpha−\beta}{\mathrm{2}}\right)={m}\:….{i}\right) \\ $$$${cos}\alpha+{cos}\beta={m} \\ $$$$\left.\mathrm{2}{cos}\left(\frac{\alpha+\beta}{\mathrm{2}}\right){cos}\left(\frac{\alpha−\beta}{\mathrm{2}}\right)={n}\:….{ii}\right) \\ $$$$\left.{i}\right)\:×{ii} \\ $$$$\mathrm{2}{sin}\left(\frac{\alpha+\beta}{\mathrm{2}}\right){cos}\left(\frac{\alpha+\beta}{\mathrm{2}}\right)\mathrm{2}{cos}^{\mathrm{2}} \left(\frac{\alpha−\beta}{\mathrm{2}}\right)={mn} \\ $$$$\Rightarrow{sin}\left(\alpha+\beta\right)=\frac{{mn}}{\mathrm{2}{cos}^{\mathrm{2}} \left(\frac{\alpha−\beta}{\mathrm{2}}\right)} \\ $$$$\:\left({i}\right)^{\mathrm{2}} +\left({ii}\right)^{\mathrm{2}} \\ $$$$\mathrm{4}{cos}^{\mathrm{2}} \left(\frac{\alpha−\beta}{\mathrm{2}}\right)\left[{sin}^{\mathrm{2}} \left(\frac{\alpha+\beta}{\mathrm{2}}\right)+{cos}^{\mathrm{2}} \left(\frac{\alpha+\beta}{\mathrm{2}}\right)\right] \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:={m}^{\mathrm{2}} +{n}^{\mathrm{2}} \\ $$$$\therefore\mathrm{2}{cos}^{\mathrm{2}} \left(\frac{\alpha−\beta}{\mathrm{2}}\right)=\frac{{m}^{\mathrm{2}} +{n}^{\mathrm{2}} }{\mathrm{2}} \\ $$$$\therefore{sin}\left(\alpha+\beta\right)=\frac{{mn}}{\mathrm{2}{cos}^{\mathrm{2}} \left(\frac{\alpha−\beta}{\mathrm{2}}\right)} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:=\frac{{mn}}{\frac{{m}^{\mathrm{2}} +{n}^{\mathrm{2}} }{\mathrm{2}}} \\ $$$$\therefore\boldsymbol{{sin}}\left(\boldsymbol{\alpha}+\boldsymbol{\beta}\right)=\frac{\mathrm{2}\boldsymbol{{mn}}}{\boldsymbol{{m}}^{\mathrm{2}} +\boldsymbol{{n}}^{\mathrm{2}} } \\ $$
Commented by infinityaction last updated on 26/Apr/22
Answered by PhysicalMath last updated on 26/Apr/22
2sin(((α+β)/2))cos(((α−β)/2))=n ... eq1 2cos(((α+β)/2))cos(((α−β)/2))=m ... eq2 =>((eq1)/(eq2)) = tan(((α+β)/2))=(n/m) sin(α+β)=((2tan(((α+β)/2)))/(1+tan^2 (((α+β)/2)))) =((2((n/m)))/(1+((n/m))^2 ))=((2mn)/(m^2 +n^2 ))
$$\mathrm{2sin}\left(\frac{\alpha+\beta}{\mathrm{2}}\right)\mathrm{cos}\left(\frac{\alpha−\beta}{\mathrm{2}}\right)={n}\:\:\:\:\:\:…\:{eq}\mathrm{1} \\ $$$$\mathrm{2cos}\left(\frac{\alpha+\beta}{\mathrm{2}}\right)\mathrm{cos}\left(\frac{\alpha−\beta}{\mathrm{2}}\right)={m}\:\:\:\:…\:{eq}\mathrm{2} \\ $$$$=>\frac{{eq}\mathrm{1}}{{eq}\mathrm{2}}\:=\:\mathrm{tan}\left(\frac{\alpha+\beta}{\mathrm{2}}\right)=\frac{{n}}{{m}} \\ $$$$\mathrm{sin}\left(\alpha+\beta\right)=\frac{\mathrm{2tan}\left(\frac{\alpha+\beta}{\mathrm{2}}\right)}{\mathrm{1}+\mathrm{tan}^{\mathrm{2}} \left(\frac{\alpha+\beta}{\mathrm{2}}\right)} \\ $$$$=\frac{\mathrm{2}\left(\frac{{n}}{{m}}\right)}{\mathrm{1}+\left(\frac{{n}}{{m}}\right)^{\mathrm{2}} }=\frac{\mathrm{2}{mn}}{{m}^{\mathrm{2}} +{n}^{\mathrm{2}} } \\ $$
Commented by peter frank last updated on 29/Apr/22
very short
$$\mathrm{very}\:\mathrm{short} \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *