solve-for-x-R-x-3-3-x-1-3-3-0-

Question Number 170389 by mr W last updated on 22/May/22

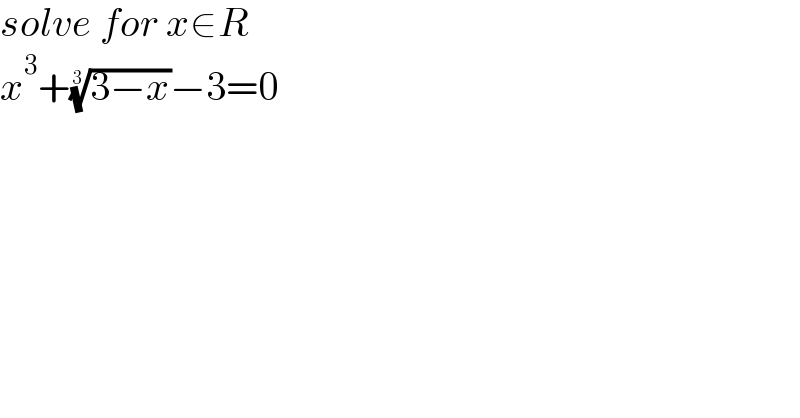
$${solve}\:{for}\:{x}\in{R} \\ $$$${x}^{\mathrm{3}} +\sqrt[{\mathrm{3}}]{\mathrm{3}−{x}}−\mathrm{3}=\mathrm{0} \\ $$

Commented by Mastermind last updated on 22/May/22

We can actually solve this by graph method Okay, Graph Details y=3−x^3 y=((3−x))^(1/3) Root ((3)^(1/3) , 0) Domain x∈R Range y∈R Vertical intercept (0, 3) Root (3, 0) Domain x∈R Range y∈R Vertical intercept (0, (3)^(1/3) )

$${We}\:{can}\:{actually}\:{solve}\:{this}\:{by}\:{graph} \\ $$$${method} \\ $$$${Okay},\:{Graph}\:{Details} \\ $$$${y}=\mathrm{3}−{x}^{\mathrm{3}} \\ $$$${y}=\sqrt[{\mathrm{3}}]{\mathrm{3}−{x}} \\ $$$$ \\ $$$${Root}\:\left(\sqrt[{\mathrm{3}}]{\mathrm{3}},\:\mathrm{0}\right) \\ $$$${Domain}\:{x}\in{R} \\ $$$${Range}\:{y}\in{R} \\ $$$${Vertical}\:{intercept}\:\left(\mathrm{0},\:\mathrm{3}\right) \\ $$$$ \\ $$$${Root}\:\left(\mathrm{3},\:\mathrm{0}\right) \\ $$$${Domain}\:{x}\in{R} \\ $$$${Range}\:{y}\in{R} \\ $$$${Vertical}\:{intercept}\:\left(\mathrm{0},\:\sqrt[{\mathrm{3}}]{\mathrm{3}}\right) \\ $$

Commented by mr W last updated on 22/May/22

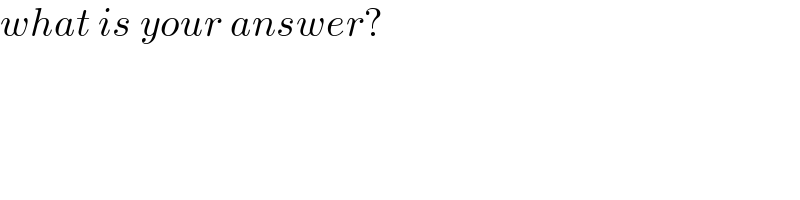
$${what}\:{is}\:{your}\:{answer}? \\ $$

Commented by Mastermind last updated on 22/May/22

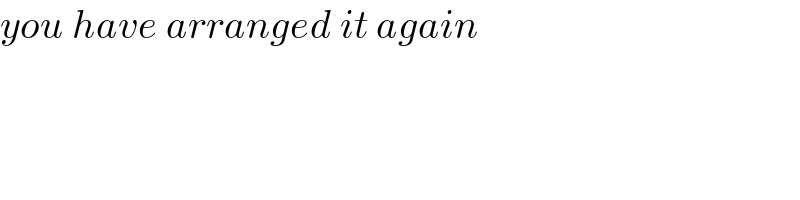
$${you}\:{have}\:{arranged}\:{it}\:{again} \\ $$

Commented by jasem1994hamoud last updated on 22/May/22

$${by}\:{whatsap}\: \\ $$$$+\mathrm{79951154287} \\ $$

Commented by mr W last updated on 22/May/22

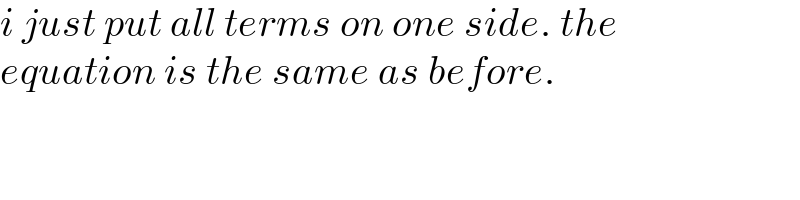
$${i}\:{just}\:{put}\:{all}\:{terms}\:{on}\:{one}\:{side}.\:{the} \\ $$$${equation}\:{is}\:{the}\:{same}\:{as}\:{before}. \\ $$

Commented by Mastermind last updated on 22/May/22

you can actually add me too +2347068402491

$${you}\:{can}\:{actually}\:{add}\:{me}\:{too} \\ $$$$+\mathrm{2347068402491} \\ $$$$ \\ $$

Commented by Mastermind last updated on 22/May/22

$${I}\:{understand} \\ $$

Answered by mr W last updated on 22/May/22

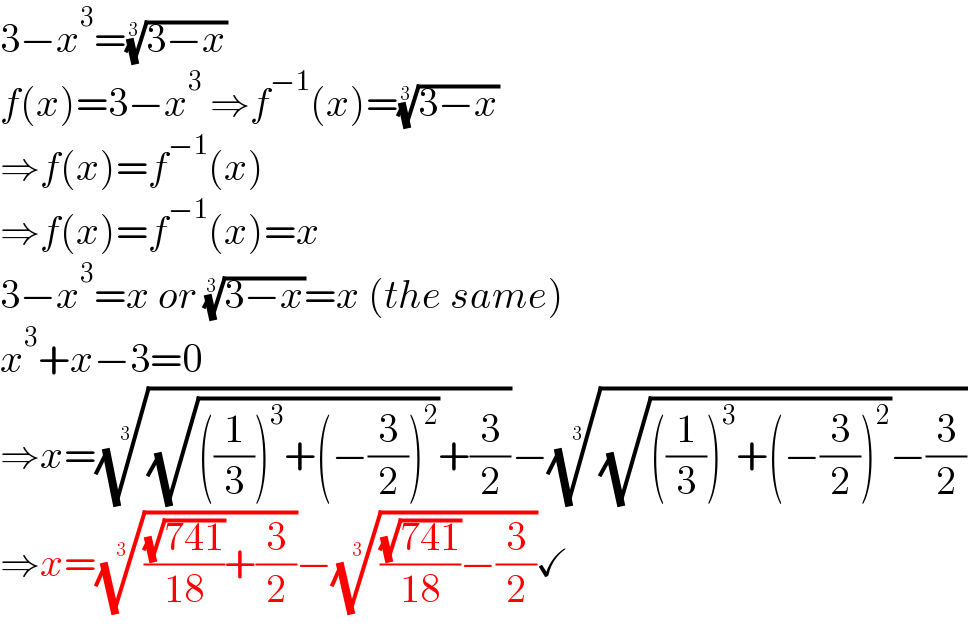
3−x^3 =((3−x))^(1/3) f(x)=3−x^3 ⇒f^(−1) (x)=((3−x))^(1/3) ⇒f(x)=f^(−1) (x) ⇒f(x)=f^(−1) (x)=x 3−x^3 =x or ((3−x))^(1/3) =x (the same) x^3 +x−3=0 ⇒x=(((√(((1/3))^3 +(−(3/2))^2 ))+(3/2)))^(1/3) −(((√(((1/3))^3 +(−(3/2))^2 ))−(3/2)))^(1/3) ⇒x=((((√(741))/(18))+(3/2)))^(1/3) −((((√(741))/(18))−(3/2)))^(1/3) ✓

$$\mathrm{3}−{x}^{\mathrm{3}} =\sqrt[{\mathrm{3}}]{\mathrm{3}−{x}} \\ $$$${f}\left({x}\right)=\mathrm{3}−{x}^{\mathrm{3}} \:\Rightarrow{f}^{−\mathrm{1}} \left({x}\right)=\sqrt[{\mathrm{3}}]{\mathrm{3}−{x}} \\ $$$$\Rightarrow{f}\left({x}\right)={f}^{−\mathrm{1}} \left({x}\right) \\ $$$$\Rightarrow{f}\left({x}\right)={f}^{−\mathrm{1}} \left({x}\right)={x} \\ $$$$\mathrm{3}−{x}^{\mathrm{3}} ={x}\:{or}\:\sqrt[{\mathrm{3}}]{\mathrm{3}−{x}}={x}\:\left({the}\:{same}\right) \\ $$$${x}^{\mathrm{3}} +{x}−\mathrm{3}=\mathrm{0} \\ $$$$\Rightarrow{x}=\sqrt[{\mathrm{3}}]{\sqrt{\left(\frac{\mathrm{1}}{\mathrm{3}}\right)^{\mathrm{3}} +\left(−\frac{\mathrm{3}}{\mathrm{2}}\right)^{\mathrm{2}} }+\frac{\mathrm{3}}{\mathrm{2}}}−\sqrt[{\mathrm{3}}]{\sqrt{\left(\frac{\mathrm{1}}{\mathrm{3}}\right)^{\mathrm{3}} +\left(−\frac{\mathrm{3}}{\mathrm{2}}\right)^{\mathrm{2}} }−\frac{\mathrm{3}}{\mathrm{2}}} \\ $$$$\Rightarrow{x}=\sqrt[{\mathrm{3}}]{\frac{\sqrt{\mathrm{741}}}{\mathrm{18}}+\frac{\mathrm{3}}{\mathrm{2}}}−\sqrt[{\mathrm{3}}]{\frac{\sqrt{\mathrm{741}}}{\mathrm{18}}−\frac{\mathrm{3}}{\mathrm{2}}}\checkmark \\ $$

Commented by Mastermind last updated on 22/May/22

$${Wow} \\ $$$${that}'{s}\:{good} \\ $$

Commented by Rasheed.Sindhi last updated on 23/May/22

$$\mathbb{G}\boldsymbol{\mathrm{reat}}\:\mathbb{S}\boldsymbol{\mathrm{ir}}! \\ $$

Commented by MJS_new last updated on 23/May/22

I think the given equation also has got a pair of complex solutions. can we find the exact values?

$$\mathrm{I}\:\mathrm{think}\:\mathrm{the}\:\mathrm{given}\:\mathrm{equation}\:\mathrm{also}\:\mathrm{has}\:\mathrm{got}\:\mathrm{a}\:\mathrm{pair} \\ $$$$\mathrm{of}\:\mathrm{complex}\:\mathrm{solutions}.\:\mathrm{can}\:\mathrm{we}\:\mathrm{find}\:\mathrm{the}\:\mathrm{exact} \\ $$$$\mathrm{values}? \\ $$

Commented by mr W last updated on 23/May/22

i′m not sure if the complex roots of x^3 +x−3=0 are also the complex roots of the original equation. i guess yes, but not sure.

$${i}'{m}\:{not}\:{sure}\:{if}\:{the}\:{complex}\:{roots}\:{of} \\ $$$${x}^{\mathrm{3}} +{x}−\mathrm{3}=\mathrm{0}\:{are}\:{also}\:{the}\:{complex}\:{roots} \\ $$$${of}\:{the}\:{original}\:{equation}.\:{i}\:{guess}\:{yes}, \\ $$$${but}\:{not}\:{sure}. \\ $$

Commented by MJS_new last updated on 23/May/22

no. I aporoximated all the roots (1) x^3 +((3−x))^(1/3) −3=0 x_1 ≈1.21341166 x_(2, 3) ≈−.597562988±.964934775i these roots don′t give a “nice”polynome: x^3 −.0182856868x^2 −1.56309342 (2) x^3 +x−3=0 x_1 ≈1.21341166 x_(2, 3) ≈−.606705831±1.45061225i (3) [(3−x)^(1/3) =3−x^3 ]^3 ⇒ x^9 −9x^6 +27x^3 −x−24=0 (x^3 +x−3)(x^6 −x^4 −6x^3 +x^2 +3x+8)=0 x^6 −4^4 +6x^3 +x^2 +3x+8=0 x_(1, 2) ≈1.54420759±.135231222i x_(3, 4) ≈−.597562988±.964934775i x_(5, 6) ≈−.946644598±1.29938754i

$$\mathrm{no}.\:\mathrm{I}\:\mathrm{aporoximated}\:\mathrm{all}\:\mathrm{the}\:\mathrm{roots} \\ $$$$\left(\mathrm{1}\right) \\ $$$${x}^{\mathrm{3}} +\sqrt[{\mathrm{3}}]{\mathrm{3}−{x}}−\mathrm{3}=\mathrm{0} \\ $$$${x}_{\mathrm{1}} \approx\mathrm{1}.\mathrm{21341166} \\ $$$${x}_{\mathrm{2},\:\mathrm{3}} \approx−.\mathrm{597562988}\pm.\mathrm{964934775i} \\ $$$$\mathrm{these}\:\mathrm{roots}\:\mathrm{don}'\mathrm{t}\:\mathrm{give}\:\mathrm{a}\:“\mathrm{nice}''\mathrm{polynome}: \\ $$$${x}^{\mathrm{3}} −.\mathrm{0182856868}{x}^{\mathrm{2}} −\mathrm{1}.\mathrm{56309342} \\ $$$$\left(\mathrm{2}\right) \\ $$$${x}^{\mathrm{3}} +{x}−\mathrm{3}=\mathrm{0} \\ $$$${x}_{\mathrm{1}} \approx\mathrm{1}.\mathrm{21341166} \\ $$$${x}_{\mathrm{2},\:\mathrm{3}} \approx−.\mathrm{606705831}\pm\mathrm{1}.\mathrm{45061225i} \\ $$$$\left(\mathrm{3}\right) \\ $$$$\left[\left(\mathrm{3}−{x}\right)^{\mathrm{1}/\mathrm{3}} =\mathrm{3}−{x}^{\mathrm{3}} \right]^{\mathrm{3}} \\ $$$$\Rightarrow \\ $$$${x}^{\mathrm{9}} −\mathrm{9}{x}^{\mathrm{6}} +\mathrm{27}{x}^{\mathrm{3}} −{x}−\mathrm{24}=\mathrm{0} \\ $$$$\left({x}^{\mathrm{3}} +{x}−\mathrm{3}\right)\left({x}^{\mathrm{6}} −{x}^{\mathrm{4}} −\mathrm{6}{x}^{\mathrm{3}} +{x}^{\mathrm{2}} +\mathrm{3}{x}+\mathrm{8}\right)=\mathrm{0} \\ $$$${x}^{\mathrm{6}} −\mathrm{4}^{\mathrm{4}} +\mathrm{6}{x}^{\mathrm{3}} +{x}^{\mathrm{2}} +\mathrm{3}{x}+\mathrm{8}=\mathrm{0} \\ $$$${x}_{\mathrm{1},\:\mathrm{2}} \approx\mathrm{1}.\mathrm{54420759}\pm.\mathrm{135231222i} \\ $$$${x}_{\mathrm{3},\:\mathrm{4}} \approx−.\mathrm{597562988}\pm.\mathrm{964934775i} \\ $$$${x}_{\mathrm{5},\:\mathrm{6}} \approx−.\mathrm{946644598}\pm\mathrm{1}.\mathrm{29938754i} \\ $$

Commented by mr W last updated on 23/May/22

$${thanks}\:{for}\:{this}\:{interesting}\:{thing}! \\ $$

Commented by Tawa11 last updated on 08/Oct/22

$$\mathrm{Great}\:\mathrm{sir} \\ $$

Facebook Tweet Pin

solve-for-x-R-x-3-3-x-1-3-3-0-

Leave a Reply Cancel reply