Question Number 40133 by maxmathsup by imad last updated on 16/Jul/18
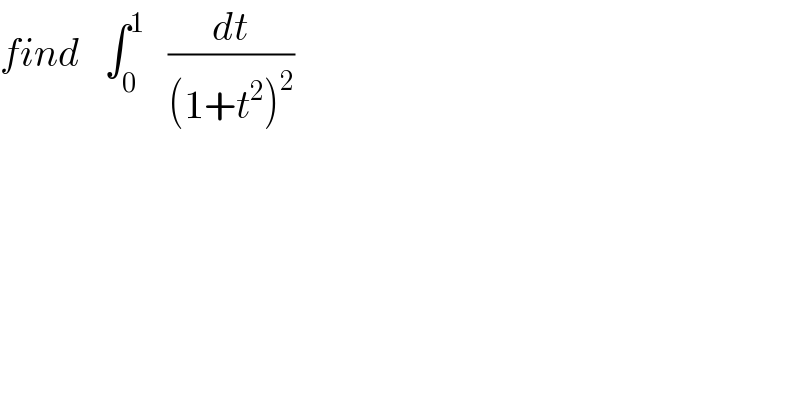
$${find}\:\:\:\int_{\mathrm{0}} ^{\mathrm{1}} \:\:\:\frac{{dt}}{\left(\mathrm{1}+{t}^{\mathrm{2}} \right)^{\mathrm{2}} } \\ $$
Commented by maxmathsup by imad last updated on 18/Jul/18
![changement t =tanθ give I = ∫_0 ^(π/4) ((1+tan^2 θ)/((1+tan^2 θ)^2 )) dθ = ∫_0 ^(π/4) (dθ/(1+tan^2 θ)) =∫_0 ^(π/4) cos^2 θ dθ = (1/2) ∫_0 ^(π/4) (1+cos(2θ)dθ =(π/8) +(1/2)[(1/2)sin(2θ)]_0 ^(π/4) =(π/8) +(1/4) ⇒ I =(π/8) +(1/4)](https://www.tinkutara.com/question/Q40266.png)
$${changement}\:{t}\:={tan}\theta\:{give}\: \\ $$$${I}\:\:=\:\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{4}}} \:\:\frac{\mathrm{1}+{tan}^{\mathrm{2}} \theta}{\left(\mathrm{1}+{tan}^{\mathrm{2}} \theta\right)^{\mathrm{2}} }\:{d}\theta\:=\:\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{4}}} \:\:\:\:\frac{{d}\theta}{\mathrm{1}+{tan}^{\mathrm{2}} \theta} \\ $$$$=\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{4}}} \:{cos}^{\mathrm{2}} \theta\:{d}\theta\:=\:\frac{\mathrm{1}}{\mathrm{2}}\:\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{4}}} \:\left(\mathrm{1}+{cos}\left(\mathrm{2}\theta\right){d}\theta\right. \\ $$$$=\frac{\pi}{\mathrm{8}}\:+\frac{\mathrm{1}}{\mathrm{2}}\left[\frac{\mathrm{1}}{\mathrm{2}}{sin}\left(\mathrm{2}\theta\right)\right]_{\mathrm{0}} ^{\frac{\pi}{\mathrm{4}}} =\frac{\pi}{\mathrm{8}}\:+\frac{\mathrm{1}}{\mathrm{4}}\:\Rightarrow \\ $$$${I}\:=\frac{\pi}{\mathrm{8}}\:+\frac{\mathrm{1}}{\mathrm{4}} \\ $$$$ \\ $$
