Question Number 171392 by cortano1 last updated on 14/Jun/22
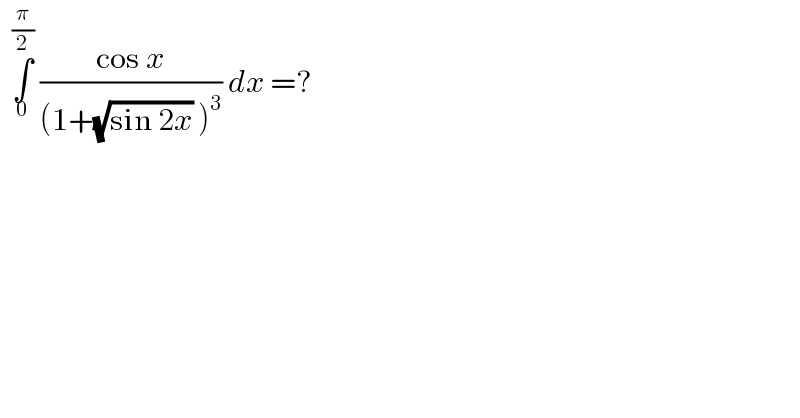
$$\:\:\underset{\mathrm{0}} {\overset{\frac{\pi}{\mathrm{2}}} {\int}}\:\frac{\mathrm{cos}\:{x}}{\left(\mathrm{1}+\sqrt{\mathrm{sin}\:\mathrm{2}{x}}\:\right)^{\mathrm{3}} }\:{dx}\:=? \\ $$
Commented by infinityaction last updated on 19/Jun/22
![I = ∫_0 ^(π/2) ((cos (π/2 − x))/(1+(√(sin 2(π/2 −x)))))dx 2I = ∫_0 ^(π/2) ((cos x +sin x)/([1+(√(1−(1−sin 2x))) ]^3 ))dx 1−sin 2x = (sin x−cos x)^2 let p = sin x−cos x → dp = cos x+sin x)dx 2I = ∫_(−1) ^1 (dp/((1+(√(1−p^2 )))^3 )) let p= sin ∅ → dp = cos ∅ d∅ I = (1/2)∫_(−π/2) ^(π/2) ((cos ∅ )/((1+cos ∅)^3 ))d∅ I=∫_0 ^(π/2) ((cos ∅)/((1+cos ∅)^3 ))d∅ t = tan ((∅/2)) I = ∫_0 ^1 (1−t^4 )dt I = (1/5)](https://www.tinkutara.com/question/Q171433.png)
$$\:\:\:\:\:\:\:{I}\:=\:\int_{\mathrm{0}} ^{\pi/\mathrm{2}} \frac{\mathrm{cos}\:\left(\pi/\mathrm{2}\:−\:{x}\right)}{\mathrm{1}+\sqrt{\mathrm{sin}\:\mathrm{2}\left(\pi/\mathrm{2}\:−{x}\right)}}{dx} \\ $$$$\:\:\:\:\:\mathrm{2}{I}\:=\:\int_{\mathrm{0}} ^{\pi/\mathrm{2}} \frac{\mathrm{cos}\:{x}\:+\mathrm{sin}\:{x}}{\left[\mathrm{1}+\sqrt{\mathrm{1}−\left(\mathrm{1}−\mathrm{sin}\:\mathrm{2}{x}\right)}\:\right]^{\mathrm{3}} \:}{dx} \\ $$$$\:\:\:\:\:\:\mathrm{1}−\mathrm{sin}\:\mathrm{2}{x}\:=\:\left(\mathrm{sin}\:{x}−\mathrm{cos}\:{x}\right)^{\mathrm{2}} \\ $$$$\:\:\:\:\:{let}\: \\ $$$$\left.{p}\:=\:\mathrm{sin}\:{x}−\mathrm{cos}\:{x}\:\rightarrow\:{dp}\:=\:\mathrm{cos}\:{x}+\mathrm{sin}\:{x}\right){dx} \\ $$$$\:\:\:\:\:\:\:\:\mathrm{2}{I}\:=\:\int_{−\mathrm{1}} ^{\mathrm{1}} \frac{{dp}}{\left(\mathrm{1}+\sqrt{\mathrm{1}−{p}^{\mathrm{2}} }\right)^{\mathrm{3}} } \\ $$$$\:\:\:\:\:\:{let}\:{p}=\:\mathrm{sin}\:\emptyset\:\:\rightarrow\:{dp}\:=\:\mathrm{cos}\:\emptyset\:{d}\emptyset \\ $$$$\:\:\:\:\:\:{I}\:=\:\frac{\mathrm{1}}{\mathrm{2}}\int_{−\pi/\mathrm{2}} ^{\pi/\mathrm{2}} \frac{\mathrm{cos}\:\emptyset\:}{\left(\mathrm{1}+\mathrm{cos}\:\emptyset\right)^{\mathrm{3}} }{d}\emptyset \\ $$$$\:\:\:\:\:{I}=\int_{\mathrm{0}} ^{\pi/\mathrm{2}} \frac{\mathrm{cos}\:\emptyset}{\left(\mathrm{1}+\mathrm{cos}\:\emptyset\right)^{\mathrm{3}} }{d}\emptyset \\ $$$$\:\:\:\:{t}\:=\:\mathrm{tan}\:\left(\frac{\emptyset}{\mathrm{2}}\right) \\ $$$$\:\:\:\:\:{I}\:=\:\int_{\mathrm{0}} ^{\mathrm{1}} \left(\mathrm{1}−{t}^{\mathrm{4}} \right){dt} \\ $$$$\:\:\:\:{I}\:\:\:=\:\:\frac{\mathrm{1}}{\mathrm{5}} \\ $$
