Question Number 171693 by cortano1 last updated on 20/Jun/22
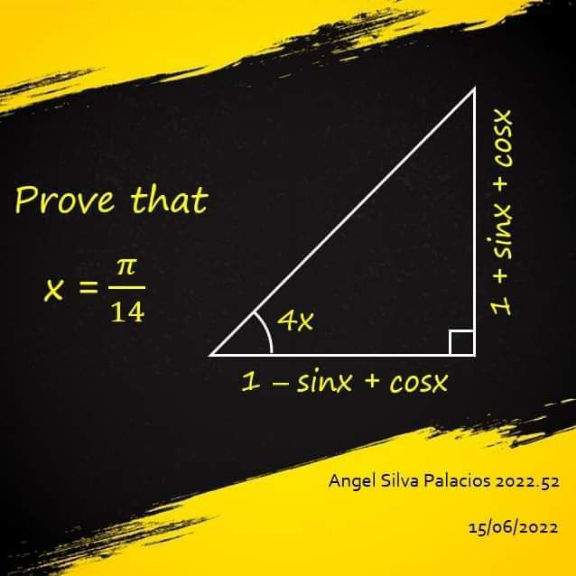
Answered by som(math1967) last updated on 20/Jun/22
![tan4x=((1+sinx+cosx)/(1−sinx+cosx)) ⇒((sin4x)/(cos4x))=((1+sinx+cosx)/(1−sinx+cosx)) ⇒sin4x−sinxsin4x+sin4xcosx =cos4x+sinxcos4x+cos4xcosx ⇒sin4x+sin4xcosx−sinxcos4x =cos4x+cos4xcosx+sin4xsinx ⇒sin4x+sin(4x−x)=cos4x+cos(4x−x) ⇒2sin((7x)/2)cos(x/2)=2cos((7x)/2)cos(x/2) ⇒ sin((7x)/2)=cos((7x)/2) [(x/2)<(π/2)] ⇒sin((7x)/2)=sin((π/2)−((7x)/2)) ⇒((7x)/2)=(π/2) −((7x)/2) ⇒ 7x=(π/2) ∴ x=(𝛑/(14))](https://www.tinkutara.com/question/Q171698.png)
$$\:\:{tan}\mathrm{4}{x}=\frac{\mathrm{1}+{sinx}+{cosx}}{\mathrm{1}−{sinx}+{cosx}} \\ $$$$\Rightarrow\frac{{sin}\mathrm{4}{x}}{{cos}\mathrm{4}{x}}=\frac{\mathrm{1}+{sinx}+{cosx}}{\mathrm{1}−{sinx}+{cosx}} \\ $$$$\Rightarrow{sin}\mathrm{4}{x}−{sinxsin}\mathrm{4}{x}+{sin}\mathrm{4}{xcosx} \\ $$$$\:\:\:\:\:={cos}\mathrm{4}{x}+{sinxcos}\mathrm{4}{x}+{cos}\mathrm{4}{xcosx} \\ $$$$\Rightarrow{sin}\mathrm{4}{x}+{sin}\mathrm{4}{xcosx}−{sinxcos}\mathrm{4}{x} \\ $$$$\:\:\:={cos}\mathrm{4}{x}+{cos}\mathrm{4}{xcosx}+{sin}\mathrm{4}{xsinx} \\ $$$$\Rightarrow{sin}\mathrm{4}{x}+{sin}\left(\mathrm{4}{x}−{x}\right)={cos}\mathrm{4}{x}+{cos}\left(\mathrm{4}{x}−{x}\right) \\ $$$$\Rightarrow\mathrm{2}{sin}\frac{\mathrm{7}{x}}{\mathrm{2}}{cos}\frac{{x}}{\mathrm{2}}=\mathrm{2}{cos}\frac{\mathrm{7}{x}}{\mathrm{2}}{cos}\frac{{x}}{\mathrm{2}} \\ $$$$\Rightarrow\:{sin}\frac{\mathrm{7}{x}}{\mathrm{2}}={cos}\frac{\mathrm{7}{x}}{\mathrm{2}}\:\:\left[\frac{{x}}{\mathrm{2}}<\frac{\pi}{\mathrm{2}}\right] \\ $$$$\Rightarrow{sin}\frac{\mathrm{7}{x}}{\mathrm{2}}={sin}\left(\frac{\pi}{\mathrm{2}}−\frac{\mathrm{7}{x}}{\mathrm{2}}\right) \\ $$$$\Rightarrow\frac{\mathrm{7}{x}}{\mathrm{2}}=\frac{\pi}{\mathrm{2}}\:−\frac{\mathrm{7}{x}}{\mathrm{2}} \\ $$$$\Rightarrow\:\mathrm{7}{x}=\frac{\pi}{\mathrm{2}} \\ $$$$\therefore\:\boldsymbol{{x}}=\frac{\boldsymbol{\pi}}{\mathrm{14}} \\ $$
Commented by cortano1 last updated on 20/Jun/22

$${nice} \\ $$
Answered by cortano1 last updated on 21/Jun/22

