Question Number 106583 by bemath last updated on 06/Aug/20
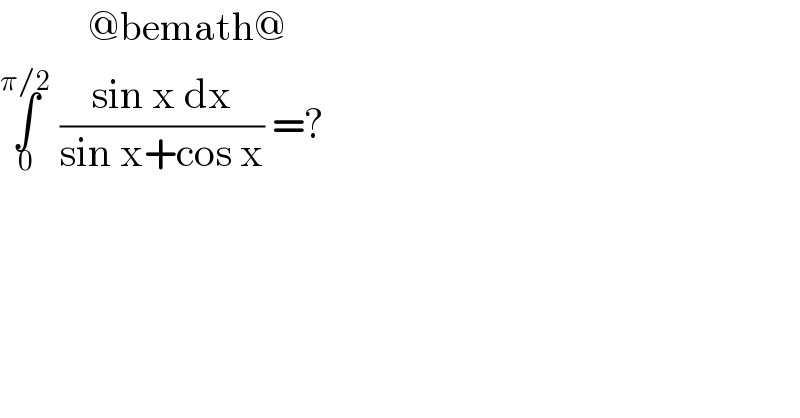
$$\:\:\:\:\:\:\:\:\:\:\:@\mathrm{bemath}@ \\ $$$$\underset{\mathrm{0}} {\overset{\pi/\mathrm{2}} {\int}}\:\frac{\mathrm{sin}\:\mathrm{x}\:\mathrm{dx}}{\mathrm{sin}\:\mathrm{x}+\mathrm{cos}\:\mathrm{x}}\:=? \\ $$
Answered by bobhans last updated on 06/Aug/20
![let a = ∫_0 ^(π/2) ((sin x dx)/(sin x+cos x)) ; ♭ = ∫_0 ^(π/2) ((cos x dx)/(sin x+cos x)) (1) a+♭ = ∫_0 ^(π/2) dx = (π/2) (2) a−♭ = ∫_0 ^(π/2) ((sin x−cos x)/(sin x+cos x)) dx = −∫_1 ^1 (du/u) = 0 [ with u = sin x+cos x ]; a = ♭ therefore a = ∫_0 ^(π/2) ((sin x dx)/(sin x+cos x)) = (1/2)×(π/2)=(π/4)](https://www.tinkutara.com/question/Q106584.png)
$$\mathrm{let}\:{a}\:=\:\underset{\mathrm{0}} {\overset{\frac{\pi}{\mathrm{2}}} {\int}}\:\frac{\mathrm{sin}\:\mathrm{x}\:\mathrm{dx}}{\mathrm{sin}\:\mathrm{x}+\mathrm{cos}\:\mathrm{x}}\:\:;\:\flat\:=\:\underset{\mathrm{0}} {\overset{\frac{\pi}{\mathrm{2}}} {\int}}\:\frac{\mathrm{cos}\:\mathrm{x}\:\mathrm{dx}}{\mathrm{sin}\:\mathrm{x}+\mathrm{cos}\:\mathrm{x}} \\ $$$$\left(\mathrm{1}\right)\:{a}+\flat\:=\:\underset{\mathrm{0}} {\overset{\frac{\pi}{\mathrm{2}}} {\int}}\:\mathrm{dx}\:=\:\frac{\pi}{\mathrm{2}}\: \\ $$$$\left(\mathrm{2}\right)\:{a}−\flat\:=\:\underset{\mathrm{0}} {\overset{\frac{\pi}{\mathrm{2}}} {\int}}\:\frac{\mathrm{sin}\:\mathrm{x}−\mathrm{cos}\:\mathrm{x}}{\mathrm{sin}\:\mathrm{x}+\mathrm{cos}\:\mathrm{x}}\:\mathrm{dx}\:=\:−\underset{\mathrm{1}} {\overset{\mathrm{1}} {\int}}\:\frac{\mathrm{du}}{\mathrm{u}}\:=\:\mathrm{0} \\ $$$$\:\left[\:\mathrm{with}\:\mathrm{u}\:=\:\mathrm{sin}\:\mathrm{x}+\mathrm{cos}\:\mathrm{x}\:\right];\:{a}\:=\:\flat \\ $$$$\mathrm{therefore}\:{a}\:=\:\underset{\mathrm{0}} {\overset{\frac{\pi}{\mathrm{2}}} {\int}}\:\frac{\mathrm{sin}\:\mathrm{x}\:\mathrm{dx}}{\mathrm{sin}\:\mathrm{x}+\mathrm{cos}\:\mathrm{x}}\:=\:\frac{\mathrm{1}}{\mathrm{2}}×\frac{\pi}{\mathrm{2}}=\frac{\pi}{\mathrm{4}} \\ $$$$ \\ $$
Commented by john santu last updated on 06/Aug/20

$$\mathrm{nice}\:\&\:\mathrm{cooll}.. \\ $$
Commented by bemath last updated on 06/Aug/20

$$\mathrm{creative}…\iddots \\ $$
