Question Number 107153 by bemath last updated on 09/Aug/20
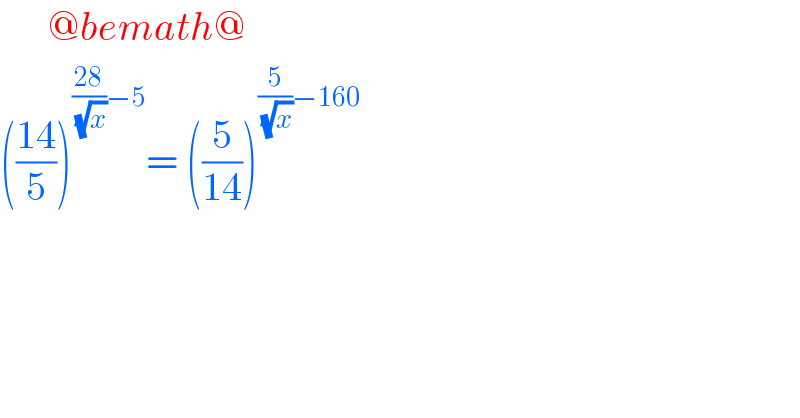
$$\:\:\:\:\:\:@{bemath}@ \\ $$$$\left(\frac{\mathrm{14}}{\mathrm{5}}\right)^{\frac{\mathrm{28}}{\:\sqrt{{x}}}−\mathrm{5}} =\:\left(\frac{\mathrm{5}}{\mathrm{14}}\right)^{\frac{\mathrm{5}}{\:\sqrt{{x}}}−\mathrm{160}} \\ $$
Answered by bobhans last updated on 09/Aug/20
![εbobhansε (((14)/5))^(((28)/( (√x)))−5) = (((14)/5))^(160−(5/( (√x)))) ⇔ ((28)/( (√x)))−5 = 160−(5/( (√x))) ; [set (1/( (√x))) = m , x>0] ⇔28m−5 = 160−5m ⇒ 33m = 165 ⇒m = 5 = (1/( (√x))) . solution x = (1/(25))](https://www.tinkutara.com/question/Q107154.png)
$$\:\:\:\:\:\:\:\varepsilon\mathrm{bobhans}\varepsilon \\ $$$$\left(\frac{\mathrm{14}}{\mathrm{5}}\right)^{\frac{\mathrm{28}}{\:\sqrt{\mathrm{x}}}−\mathrm{5}} =\:\left(\frac{\mathrm{14}}{\mathrm{5}}\right)^{\mathrm{160}−\frac{\mathrm{5}}{\:\sqrt{\mathrm{x}}}} \\ $$$$\Leftrightarrow\:\frac{\mathrm{28}}{\:\sqrt{\mathrm{x}}}−\mathrm{5}\:=\:\mathrm{160}−\frac{\mathrm{5}}{\:\sqrt{\mathrm{x}}}\:;\:\left[\mathrm{set}\:\frac{\mathrm{1}}{\:\sqrt{\mathrm{x}}}\:=\:\mathrm{m}\:,\:\mathrm{x}>\mathrm{0}\right] \\ $$$$\Leftrightarrow\mathrm{28m}−\mathrm{5}\:=\:\mathrm{160}−\mathrm{5m} \\ $$$$\:\Rightarrow\:\mathrm{33m}\:=\:\mathrm{165}\:\Rightarrow\mathrm{m}\:=\:\mathrm{5}\:=\:\frac{\mathrm{1}}{\:\sqrt{\mathrm{x}}}\:.\:\mathrm{solution}\:\mathrm{x}\:=\:\frac{\mathrm{1}}{\mathrm{25}} \\ $$
