Question Number 42188 by maxmathsup by imad last updated on 19/Aug/18
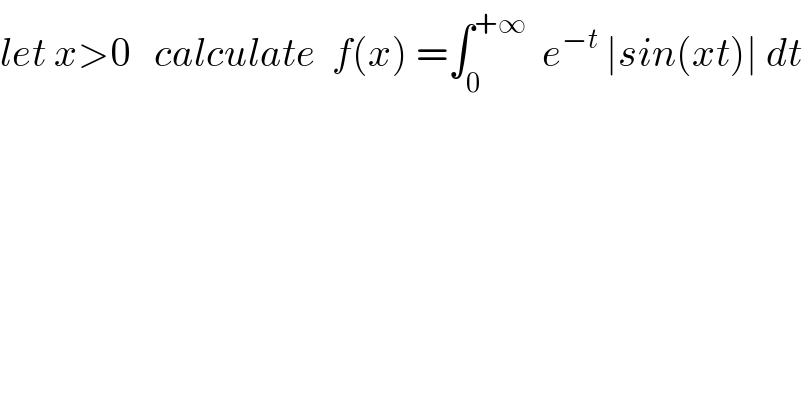
$${let}\:{x}>\mathrm{0}\:\:\:{calculate}\:\:{f}\left({x}\right)\:=\int_{\mathrm{0}} ^{+\infty} \:\:{e}^{−{t}} \:\mid{sin}\left({xt}\right)\mid\:{dt} \\ $$
Commented by maxmathsup by imad last updated on 23/Aug/18
![changement xt =u give f(x) =∫_0 ^∞ e^(−(u/x)) ∣sin(u)∣(du/x) =(1/x) ∫_0 ^∞ e^(−(u/x)) ∣sin(u)∣du ⇒xf(x)=Σ_(n=0) ^∞ ∫_(nπ) ^((n+1)π) e^(−(u/x)) ∣sinu∣ du =_(u =nπ +t) Σ_(n=0) ^∞ ∫_0 ^π e^(−((nπ+t)/x)) ∣sin(nπ+t)∣dt =Σ_(n=0) ^∞ ∫_0 ^π e^(−((nπ)/x)) e^(t/x) sint dt =Σ_(n=0) ^∞ e^(−((nπ)/x)) ∫_0 ^π e^(t/x) sint dt but ∫_0 ^π e^(t/x) sint dt = Im( ∫_0 ^π e^((t/x)+it) dt) and ∫_0 ^π e^(((1/x)+i)t) dt =[(1/((1/x)+i)) e^(((1/x)+i)t) ]_0 ^π =(x/(1+xi)){ e^((π/x) +iπ) −1}=((x(1−xi))/(1+x^2 )){−e^(π/x) −1} =((x(−1+xi)(1+e^(π/x) ))/(1+x^2 )) =((1+e^(π/x) )/(1+x^2 ))(−x +x^2 i) ⇒∫_0 ^π e^(t/x) sint dt=(x^2 /(1+x^2 ))(1+e^(π/x) ) ⇒ xf(x)=(x^2 /(1+x^2 ))(1+e^(π/x) )Σ_(n=0) ^∞ (e^(−(π/x)) )^n =(x^2 /(1+x^2 ))(1+e^(π/x) ) (1/(1−e^(−(π/x)) )) ⇒ xf(x) =(x^2 /(1+x^2 )) ((1+e^(π/x) )/(1−e^(−(π/x)) )) ⇒ f(x)= (x/(1+x^2 )) ((1+e^(π/x) )/(1−e^(−(π/x)) )) .](https://www.tinkutara.com/question/Q42325.png)
$${changement}\:{xt}\:={u}\:{give}\:\:{f}\left({x}\right)\:=\int_{\mathrm{0}} ^{\infty} \:\:{e}^{−\frac{{u}}{{x}}} \:\mid{sin}\left({u}\right)\mid\frac{{du}}{{x}} \\ $$$$=\frac{\mathrm{1}}{{x}}\:\int_{\mathrm{0}} ^{\infty} \:{e}^{−\frac{{u}}{{x}}} \:\mid{sin}\left({u}\right)\mid{du}\:\Rightarrow{xf}\left({x}\right)=\sum_{{n}=\mathrm{0}} ^{\infty} \:\:\int_{{n}\pi} ^{\left({n}+\mathrm{1}\right)\pi} \:{e}^{−\frac{{u}}{{x}}} \:\mid{sinu}\mid\:{du} \\ $$$$=_{{u}\:={n}\pi\:+{t}} \:\:\sum_{{n}=\mathrm{0}} ^{\infty} \:\:\int_{\mathrm{0}} ^{\pi} \:\:{e}^{−\frac{{n}\pi+{t}}{{x}}} \:\:\mid{sin}\left({n}\pi+{t}\right)\mid{dt} \\ $$$$=\sum_{{n}=\mathrm{0}} ^{\infty} \:\:\int_{\mathrm{0}} ^{\pi} \:\:{e}^{−\frac{{n}\pi}{{x}}} \:{e}^{\frac{{t}}{{x}}} \:\:{sint}\:{dt}\:=\sum_{{n}=\mathrm{0}} ^{\infty} \:\:{e}^{−\frac{{n}\pi}{{x}}} \:\:\int_{\mathrm{0}} ^{\pi} \:\:{e}^{\frac{{t}}{{x}}} \:{sint}\:{dt}\:{but} \\ $$$$\int_{\mathrm{0}} ^{\pi} \:\:{e}^{\frac{{t}}{{x}}} \:{sint}\:{dt}\:=\:{Im}\left(\:\int_{\mathrm{0}} ^{\pi} \:\:{e}^{\frac{{t}}{{x}}+{it}} \:{dt}\right)\:{and}\:\:\:\int_{\mathrm{0}} ^{\pi} \:\:{e}^{\left(\frac{\mathrm{1}}{{x}}+{i}\right){t}} {dt} \\ $$$$=\left[\frac{\mathrm{1}}{\frac{\mathrm{1}}{{x}}+{i}}\:{e}^{\left(\frac{\mathrm{1}}{{x}}+{i}\right){t}} \right]_{\mathrm{0}} ^{\pi} \:=\frac{{x}}{\mathrm{1}+{xi}}\left\{\:{e}^{\frac{\pi}{{x}}\:+{i}\pi} \:−\mathrm{1}\right\}=\frac{{x}\left(\mathrm{1}−{xi}\right)}{\mathrm{1}+{x}^{\mathrm{2}} }\left\{−{e}^{\frac{\pi}{{x}}} \:−\mathrm{1}\right\} \\ $$$$=\frac{{x}\left(−\mathrm{1}+{xi}\right)\left(\mathrm{1}+{e}^{\frac{\pi}{{x}}} \right)}{\mathrm{1}+{x}^{\mathrm{2}} }\:=\frac{\mathrm{1}+{e}^{\frac{\pi}{{x}}} }{\mathrm{1}+{x}^{\mathrm{2}} }\left(−{x}\:+{x}^{\mathrm{2}} {i}\right)\:\Rightarrow\int_{\mathrm{0}} ^{\pi} \:{e}^{\frac{{t}}{{x}}} \:{sint}\:{dt}=\frac{{x}^{\mathrm{2}} }{\mathrm{1}+{x}^{\mathrm{2}} }\left(\mathrm{1}+{e}^{\frac{\pi}{{x}}} \right)\:\Rightarrow \\ $$$${xf}\left({x}\right)=\frac{{x}^{\mathrm{2}} }{\mathrm{1}+{x}^{\mathrm{2}} }\left(\mathrm{1}+{e}^{\frac{\pi}{{x}}} \right)\sum_{{n}=\mathrm{0}} ^{\infty} \:\left({e}^{−\frac{\pi}{{x}}} \right)^{{n}} \:=\frac{{x}^{\mathrm{2}} }{\mathrm{1}+{x}^{\mathrm{2}} }\left(\mathrm{1}+{e}^{\frac{\pi}{{x}}} \right)\:\frac{\mathrm{1}}{\mathrm{1}−{e}^{−\frac{\pi}{{x}}} }\:\Rightarrow \\ $$$${xf}\left({x}\right)\:=\frac{{x}^{\mathrm{2}} }{\mathrm{1}+{x}^{\mathrm{2}} }\:\frac{\mathrm{1}+{e}^{\frac{\pi}{{x}}} }{\mathrm{1}−{e}^{−\frac{\pi}{{x}}} }\:\:\Rightarrow\:{f}\left({x}\right)=\:\frac{{x}}{\mathrm{1}+{x}^{\mathrm{2}} }\:\frac{\mathrm{1}+{e}^{\frac{\pi}{{x}}} }{\mathrm{1}−{e}^{−\frac{\pi}{{x}}} }\:. \\ $$$$ \\ $$
