Question Number 42367 by Joel578 last updated on 24/Aug/18
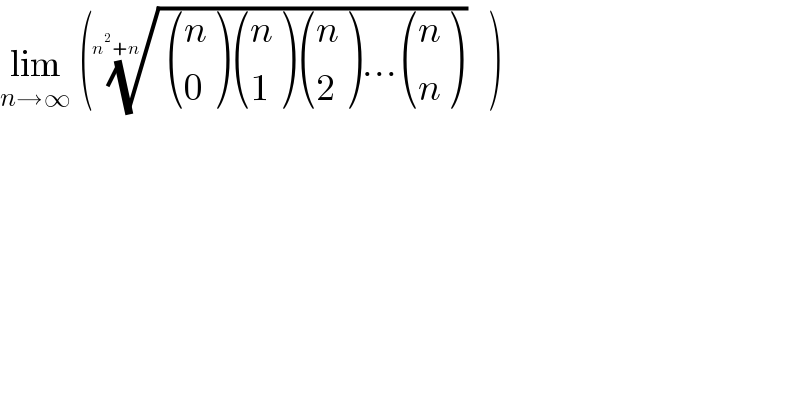
$$\underset{{n}\rightarrow\infty} {\mathrm{lim}}\:\left(\sqrt[{{n}^{\mathrm{2}} +{n}}]{\:\begin{pmatrix}{{n}}\\{\mathrm{0}}\end{pmatrix}\begin{pmatrix}{{n}}\\{\mathrm{1}}\end{pmatrix}\begin{pmatrix}{{n}}\\{\mathrm{2}}\end{pmatrix}…\begin{pmatrix}{{n}}\\{{n}}\end{pmatrix}}\right) \\ $$
Answered by tanmay.chaudhury50@gmail.com last updated on 24/Aug/18
![T_n =nc_0 ×nc_1 ×nc_2 ...×nc_n T_n =((n!)/(0!(n−0)!))×((n!)/(1!(n−1)!))×((n!)/(2!(n−2)!))×...×((n!)/(n!(n−n)!)) T_n =(((n!)^n )/((0!×1!×2!×3!..×n!){(n−0)!×(n−1)!×(n−2)!×..×(n−n)!})) T_n =(((n!)^2 )/((1!×2!×3!...×n!)^2 )) T_n =(1/((((1!)/(n!))×((2!)/(n!))×((3!)/(n!))×...×((n!)/(n!)))^2 )) lim_(n→∞) [(1/((((1!)/(n!))×((2!)/(n!))×((3!)/(n!))×...×((n!)/(n!)))^2 ))]^(1/(n^2 +n)) contd...](https://www.tinkutara.com/question/Q42389.png)
$${T}_{{n}} ={nc}_{\mathrm{0}} ×{nc}_{\mathrm{1}} ×{nc}_{\mathrm{2}} …×{nc}_{{n}} \\ $$$${T}_{{n}} =\frac{{n}!}{\mathrm{0}!\left({n}−\mathrm{0}\right)!}×\frac{{n}!}{\mathrm{1}!\left({n}−\mathrm{1}\right)!}×\frac{{n}!}{\mathrm{2}!\left({n}−\mathrm{2}\right)!}×…×\frac{{n}!}{{n}!\left({n}−{n}\right)!} \\ $$$${T}_{{n}} =\frac{\left({n}!\right)^{{n}} }{\left(\mathrm{0}!×\mathrm{1}!×\mathrm{2}!×\mathrm{3}!..×{n}!\right)\left\{\left({n}−\mathrm{0}\right)!×\left({n}−\mathrm{1}\right)!×\left({n}−\mathrm{2}\right)!×..×\left({n}−{n}\right)!\right\}} \\ $$$${T}_{{n}} =\frac{\left({n}!\right)^{\mathrm{2}} }{\left(\mathrm{1}!×\mathrm{2}!×\mathrm{3}!…×{n}!\right)^{\mathrm{2}} } \\ $$$${T}_{{n}} =\frac{\mathrm{1}}{\left(\frac{\mathrm{1}!}{{n}!}×\frac{\mathrm{2}!}{{n}!}×\frac{\mathrm{3}!}{{n}!}×…×\frac{{n}!}{{n}!}\right)^{\mathrm{2}} } \\ $$$${li}\underset{{n}\rightarrow\infty} {{m}}\:\left[\frac{\mathrm{1}}{\left(\frac{\mathrm{1}!}{{n}!}×\frac{\mathrm{2}!}{{n}!}×\frac{\mathrm{3}!}{{n}!}×…×\frac{{n}!}{{n}!}\right)^{\mathrm{2}} }\right]^{\frac{\mathrm{1}}{{n}^{\mathrm{2}} +{n}}} \\ $$$${contd}… \\ $$
