Question Number 108262 by 675480065 last updated on 15/Aug/20
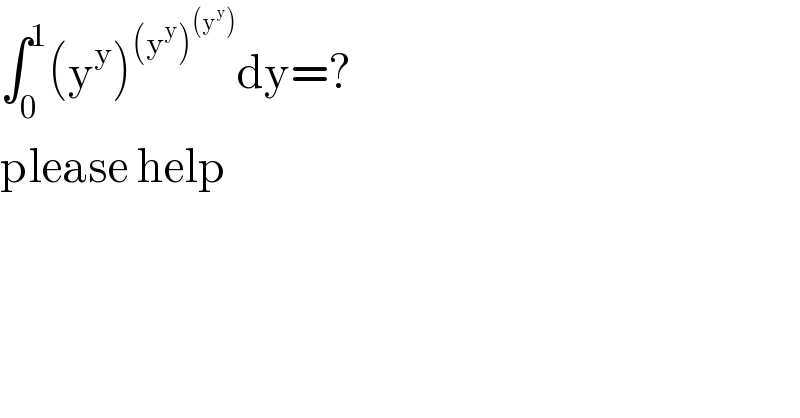
$$\int_{\mathrm{0}} ^{\mathrm{1}} \left(\mathrm{y}^{\mathrm{y}} \right)^{\left(\mathrm{y}^{\mathrm{y}} \right)^{\left(\mathrm{y}^{\mathrm{y}} \right)} } \mathrm{dy}=? \\ $$$$\mathrm{please}\:\mathrm{help} \\ $$
Answered by mathdave last updated on 15/Aug/20

$${answer}\:{is}\:\frac{\pi}{\mathrm{12}} \\ $$
Commented by 675480065 last updated on 15/Aug/20

$$\mathrm{solution}\:\mathrm{pls} \\ $$
Answered by mathdave last updated on 16/Aug/20
![solution let x=∫_0 ^1 (y^y )^((y^y )^((y^y )^.^.^(..^• ) ) ) dy therefor x=y^(yx ) let t=yx (t/y)=y^(y×(t/y)) =y^t and x=(t/y) t=y^t .y=y^(t+1) den y=t^(1/(1+t)) ..............(1) but x=(t/y)=t^(t/(1/(1+t))) =t.t^(−(1/(1+t))) ∵ x=t^((1−(1/(1+t)))) ..........(2) but I=∫_0 ^1 xdy=∫_0 ^1 t^((1−(1/(1+t)))) (d/dt)(t^(1/(1+t)) )dt since y^(1/(1+t)) logging both side and differentiate using product formular (d/dt)(lny)=(1/(1+t)).(d/dt)(lnt)+lnt(d/dt)((1/(1+t))) (1/y)(dy/dt)=[(1/(t(1+t)))−((lnt)/((1+t)^2 ))]=y[(1/(t(1+t)))−((lnt)/((1+t)^2 ))] (dy/dt)=t^(1/(1+t)) [(1/(t(1+t)))−((lnt)/((1+t)^2 ))] then putting back I=∫_0 ^1 t^(t/(1+t)) .t^(1/(1+t)) .(1/t)[(1/(1+t))−((tlnt)/((1+t)^2 ))]dt=∫_0 ^1 t.t^(−1) [(1/(1+t))−((tlnt)/((1+t)^2 ))]dt I=∫_0 ^1 ((1/(1+t)))dt−∫_0 ^1 ((tlnt)/((1+t)^2 ))dt I=ln(1+t)∣_0 ^1 −∫_0 ^1 ((tlnt)/((1+t)^2 ))dt=ln2−∫_0 ^1 (((t+1−1))/((1+t)^2 ))lntdt I_(AB) =ln2−[∫_0 ^1 (((1+t)lnt)/((1+t)^2 ))dt−∫_0 ^1 ((lnt)/((1+t)^2 ))dt] by solving B using I.B.p ∫_0 ^1 ((lnt)/((1+t)^2 ))dt=−((lnt)/(1+t))∣_0 ^1 +∫_0 ^1 (1/(1+t))dt=∫_0 ^1 ((1/t)−(1/(1+t)))dt =∫_0 ^1 (1/t)dt−∫_0 ^1 (1/(1+t))dt=lnt∣_0 ^1 −ln(1+t)∣_0 ^1 ∵ I_B =−ln2 and solving I_A using I.B.P I_A =∫_0 ^1 ((lnt)/(1+t))dt=ln(1+t)lnt∣_0 ^1 −∫_0 ^1 ((ln(1+t))/t)dt using maclaurin′s series ln(1+t)=(−1)^(n−1) Σ_(n=1) ^∞ (t^n /n)=−∫_0 ^1 Σ_(n=1) ^∞ (((−1)^(n−1) t^n )/n).(1/t)dt I_(A=) =−Σ_(n=1) ^∞ (((−1)^(n−1) )/n)∫_0 ^1 t^(n−1) dt=−Σ_(n=1) ^∞ (((−1)^(n−1) )/n)[(t^(n−1+1) /(n−1+1))]_0 ^1 I_A =−Σ_(n=1) ^∞ (((−1)^(n−1) )/n^2 )=−η(2)=−(π^2 /(12)) but I=ln2−I_(AB) =ln2−[−(π^2 /(12))−(−ln2)] I=ln2+(π^2 /(12))−ln2=(π^2 /(12)) ∵I=∫_0 ^1 (y^y )^((y^y )^((y^y )) ) dy=(π^2 /(12)) solution by mathdave 15/08/2020](https://www.tinkutara.com/question/Q108281.png)
$${solution} \\ $$$${let}\:{x}=\int_{\mathrm{0}} ^{\mathrm{1}} \left({y}^{{y}} \right)^{\left({y}^{{y}} \right)^{\left({y}^{{y}} \right)^{.^{.^{..^{\bullet} } } } } } {dy}\:\:\:\:{therefor}\:\:{x}={y}^{{yx}\:} {let}\:\:\:{t}={yx} \\ $$$$\frac{{t}}{{y}}={y}^{{y}×\frac{{t}}{{y}}} ={y}^{{t}} \:{and}\:{x}=\frac{{t}}{{y}} \\ $$$${t}={y}^{{t}} .{y}={y}^{{t}+\mathrm{1}} \:\:\:\:{den}\:\:{y}={t}^{\frac{\mathrm{1}}{\mathrm{1}+{t}}} …………..\left(\mathrm{1}\right) \\ $$$${but}\:{x}=\frac{{t}}{{y}}={t}^{\frac{{t}}{\frac{\mathrm{1}}{\mathrm{1}+{t}}}} ={t}.{t}^{−\frac{\mathrm{1}}{\mathrm{1}+{t}}} \:\:\:\:\:\because\:\:{x}={t}^{\left(\mathrm{1}−\frac{\mathrm{1}}{\mathrm{1}+{t}}\right)} ……….\left(\mathrm{2}\right) \\ $$$${but}\:{I}=\int_{\mathrm{0}} ^{\mathrm{1}} {xdy}=\int_{\mathrm{0}} ^{\mathrm{1}} {t}^{\left(\mathrm{1}−\frac{\mathrm{1}}{\mathrm{1}+{t}}\right)} \frac{{d}}{{dt}}\left({t}^{\frac{\mathrm{1}}{\mathrm{1}+{t}}} \right){dt} \\ $$$${since}\:\:{y}^{\frac{\mathrm{1}}{\mathrm{1}+{t}}} \:\:{logging}\:{both}\:{side}\:\:{and}\:{differentiate} \\ $$$${using}\:{product}\:{formular} \\ $$$$\frac{{d}}{{dt}}\left(\mathrm{ln}{y}\right)=\frac{\mathrm{1}}{\mathrm{1}+{t}}.\frac{{d}}{{dt}}\left(\mathrm{ln}{t}\right)+\mathrm{ln}{t}\frac{{d}}{{dt}}\left(\frac{\mathrm{1}}{\mathrm{1}+{t}}\right) \\ $$$$\frac{\mathrm{1}}{{y}}\frac{{dy}}{{dt}}=\left[\frac{\mathrm{1}}{{t}\left(\mathrm{1}+{t}\right)}−\frac{\mathrm{ln}{t}}{\left(\mathrm{1}+{t}\right)^{\mathrm{2}} }\right]={y}\left[\frac{\mathrm{1}}{{t}\left(\mathrm{1}+{t}\right)}−\frac{\mathrm{ln}{t}}{\left(\mathrm{1}+{t}\right)^{\mathrm{2}} }\right] \\ $$$$\frac{{dy}}{{dt}}={t}^{\frac{\mathrm{1}}{\mathrm{1}+{t}}} \left[\frac{\mathrm{1}}{{t}\left(\mathrm{1}+{t}\right)}−\frac{\mathrm{ln}{t}}{\left(\mathrm{1}+{t}\right)^{\mathrm{2}} }\right]\:\:\:\:{then}\:{putting}\:\:{back} \\ $$$${I}=\int_{\mathrm{0}} ^{\mathrm{1}} {t}^{\frac{{t}}{\mathrm{1}+{t}}} .{t}^{\frac{\mathrm{1}}{\mathrm{1}+{t}}} .\frac{\mathrm{1}}{{t}}\left[\frac{\mathrm{1}}{\mathrm{1}+{t}}−\frac{{t}\mathrm{ln}{t}}{\left(\mathrm{1}+{t}\right)^{\mathrm{2}} }\right]{dt}=\int_{\mathrm{0}} ^{\mathrm{1}} {t}.{t}^{−\mathrm{1}} \left[\frac{\mathrm{1}}{\mathrm{1}+{t}}−\frac{{t}\mathrm{ln}{t}}{\left(\mathrm{1}+{t}\right)^{\mathrm{2}} }\right]{dt} \\ $$$${I}=\int_{\mathrm{0}} ^{\mathrm{1}} \left(\frac{\mathrm{1}}{\mathrm{1}+{t}}\right){dt}−\int_{\mathrm{0}} ^{\mathrm{1}} \frac{{t}\mathrm{ln}{t}}{\left(\mathrm{1}+{t}\right)^{\mathrm{2}} }{dt} \\ $$$${I}=\mathrm{ln}\left(\mathrm{1}+{t}\right)\mid_{\mathrm{0}} ^{\mathrm{1}} −\int_{\mathrm{0}} ^{\mathrm{1}} \frac{{t}\mathrm{ln}{t}}{\left(\mathrm{1}+{t}\right)^{\mathrm{2}} }{dt}=\mathrm{ln2}−\int_{\mathrm{0}} ^{\mathrm{1}} \frac{\left({t}+\mathrm{1}−\mathrm{1}\right)}{\left(\mathrm{1}+{t}\right)^{\mathrm{2}} }\mathrm{ln}{tdt} \\ $$$${I}_{{AB}} =\mathrm{ln2}−\left[\int_{\mathrm{0}} ^{\mathrm{1}} \frac{\left(\mathrm{1}+{t}\right)\mathrm{ln}{t}}{\left(\mathrm{1}+{t}\right)^{\mathrm{2}} }{dt}−\int_{\mathrm{0}} ^{\mathrm{1}} \frac{\mathrm{ln}{t}}{\left(\mathrm{1}+{t}\right)^{\mathrm{2}} }{dt}\right] \\ $$$${by}\:{solving}\:{B}\:{using}\:{I}.{B}.{p} \\ $$$$\int_{\mathrm{0}} ^{\mathrm{1}} \frac{\mathrm{ln}{t}}{\left(\mathrm{1}+{t}\right)^{\mathrm{2}} }{dt}=−\frac{\mathrm{ln}{t}}{\mathrm{1}+{t}}\mid_{\mathrm{0}} ^{\mathrm{1}} +\int_{\mathrm{0}} ^{\mathrm{1}} \frac{\mathrm{1}}{\mathrm{1}+{t}}{dt}=\int_{\mathrm{0}} ^{\mathrm{1}} \left(\frac{\mathrm{1}}{{t}}−\frac{\mathrm{1}}{\mathrm{1}+{t}}\right){dt} \\ $$$$=\int_{\mathrm{0}} ^{\mathrm{1}} \frac{\mathrm{1}}{{t}}{dt}−\int_{\mathrm{0}} ^{\mathrm{1}} \frac{\mathrm{1}}{\mathrm{1}+{t}}{dt}=\mathrm{ln}{t}\mid_{\mathrm{0}} ^{\mathrm{1}} −\mathrm{ln}\left(\mathrm{1}+{t}\right)\mid_{\mathrm{0}} ^{\mathrm{1}} \\ $$$$\because\:{I}_{{B}} =−\mathrm{ln2}\:\:\:\:\:{and}\:{solving}\:{I}_{{A}} \:\:{using}\:{I}.{B}.{P} \\ $$$${I}_{{A}} =\int_{\mathrm{0}} ^{\mathrm{1}} \frac{\mathrm{ln}{t}}{\mathrm{1}+{t}}{dt}=\mathrm{ln}\left(\mathrm{1}+{t}\right)\mathrm{ln}{t}\mid_{\mathrm{0}} ^{\mathrm{1}} −\int_{\mathrm{0}} ^{\mathrm{1}} \frac{\mathrm{ln}\left(\mathrm{1}+{t}\right)}{{t}}{dt} \\ $$$${using}\:{maclaurin}'{s}\:{series}\: \\ $$$$\mathrm{ln}\left(\mathrm{1}+{t}\right)=\left(−\mathrm{1}\right)^{{n}−\mathrm{1}} \underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{{t}^{{n}} }{{n}}=−\int_{\mathrm{0}} ^{\mathrm{1}} \underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{\left(−\mathrm{1}\right)^{{n}−\mathrm{1}} {t}^{{n}} }{{n}}.\frac{\mathrm{1}}{{t}}{dt} \\ $$$${I}_{{A}=} =−\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{\left(−\mathrm{1}\right)^{{n}−\mathrm{1}} }{{n}}\int_{\mathrm{0}} ^{\mathrm{1}} {t}^{{n}−\mathrm{1}} {dt}=−\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{\left(−\mathrm{1}\right)^{{n}−\mathrm{1}} }{{n}}\left[\frac{{t}^{{n}−\mathrm{1}+\mathrm{1}} }{{n}−\mathrm{1}+\mathrm{1}}\right]_{\mathrm{0}} ^{\mathrm{1}} \\ $$$${I}_{{A}} =−\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{\left(−\mathrm{1}\right)^{{n}−\mathrm{1}} }{{n}^{\mathrm{2}} }=−\eta\left(\mathrm{2}\right)=−\frac{\pi^{\mathrm{2}} }{\mathrm{12}} \\ $$$${but}\:{I}=\mathrm{ln2}−{I}_{{AB}} =\mathrm{ln2}−\left[−\frac{\pi^{\mathrm{2}} }{\mathrm{12}}−\left(−\mathrm{ln2}\right)\right] \\ $$$${I}=\mathrm{ln2}+\frac{\pi^{\mathrm{2}} }{\mathrm{12}}−\mathrm{ln2}=\frac{\pi^{\mathrm{2}} }{\mathrm{12}} \\ $$$$\because{I}=\int_{\mathrm{0}} ^{\mathrm{1}} \left({y}^{{y}} \right)^{\left({y}^{{y}} \right)^{\left({y}^{{y}} \right)} } {dy}=\frac{\pi^{\mathrm{2}} }{\mathrm{12}} \\ $$$${solution}\:{by}\:{mathdave} \\ $$$$\mathrm{15}/\mathrm{08}/\mathrm{2020} \\ $$
Commented by Her_Majesty last updated on 18/Aug/20

$${I}\:{don}'{t}\:{think}\:{this}\:{is}\:{true}.\:{the}\:{value}\:{of}\:{the} \\ $$$${integral}\:{is}\:{slightly}\:{less}\:{than}\:\pi^{\mathrm{2}} /\mathrm{12} \\ $$$$\pi^{\mathrm{2}} /\mathrm{12}\approx.\mathrm{822467033424} \\ $$$${but}\:{I}\approx.\mathrm{820108872462} \\ $$
