x-y-1-x-5-xy-y-5-x-2-y-2-faind-the-volue-of-x-2022-xy-y-2022-

Question Number 174029 by mathlove last updated on 23/Jul/22

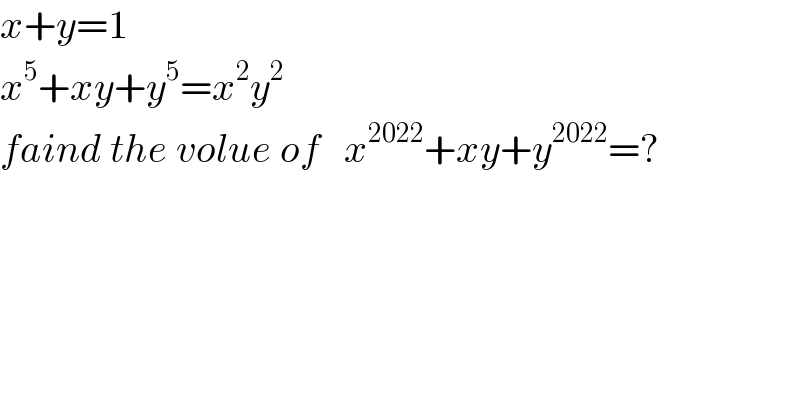
$${x}+{y}=\mathrm{1} \\ $$$${x}^{\mathrm{5}} +{xy}+{y}^{\mathrm{5}} ={x}^{\mathrm{2}} {y}^{\mathrm{2}\:\:\:\:\:\:} \\ $$$${faind}\:{the}\:{volue}\:{of}\:\:\:{x}^{\mathrm{2022}} +{xy}+{y}^{\mathrm{2022}} =? \\ $$

Commented by MJS_new last updated on 23/Jul/22

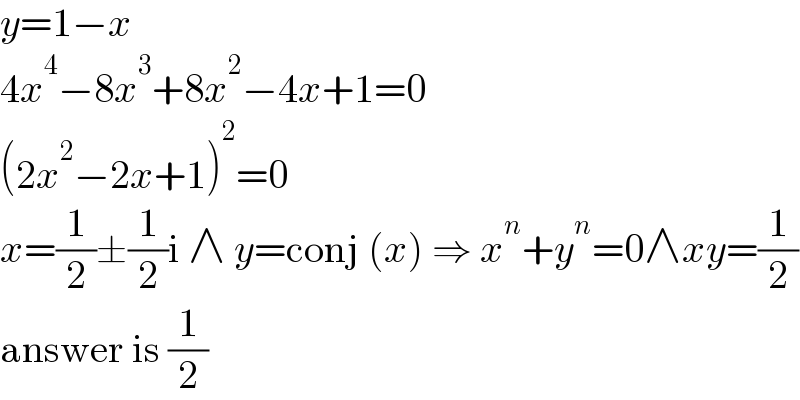
y=1−x 4x^4 −8x^3 +8x^2 −4x+1=0 (2x^2 −2x+1)^2 =0 x=(1/2)±(1/2)i ∧ y=conj (x) ⇒ x^n +y^n =0∧xy=(1/2) answer is (1/2)

$${y}=\mathrm{1}−{x} \\ $$$$\mathrm{4}{x}^{\mathrm{4}} −\mathrm{8}{x}^{\mathrm{3}} +\mathrm{8}{x}^{\mathrm{2}} −\mathrm{4}{x}+\mathrm{1}=\mathrm{0} \\ $$$$\left(\mathrm{2}{x}^{\mathrm{2}} −\mathrm{2}{x}+\mathrm{1}\right)^{\mathrm{2}} =\mathrm{0} \\ $$$${x}=\frac{\mathrm{1}}{\mathrm{2}}\pm\frac{\mathrm{1}}{\mathrm{2}}\mathrm{i}\:\wedge\:{y}=\mathrm{conj}\:\left({x}\right)\:\Rightarrow\:{x}^{{n}} +{y}^{{n}} =\mathrm{0}\wedge{xy}=\frac{\mathrm{1}}{\mathrm{2}} \\ $$$$\mathrm{answer}\:\mathrm{is}\:\frac{\mathrm{1}}{\mathrm{2}} \\ $$

Answered by mr W last updated on 23/Jul/22

x^2 +y^2 +2xy=1 x^2 +y^2 =1−2xy (x^2 +y^2 )(x+y)=1−2xy x^3 +y^3 +xy(x+y)=1−2xy x^3 +y^3 =1−3xy x^4 +y^4 +2(xy)^2 =1−4xy+4(xy)^2 x^4 +y^4 =1−4xy+2(xy)^2 (x^4 +y^4 )(x+y)=1−4xy+2(xy)^2 x^5 +y^5 +xy(x^3 +y^3 )=1−4xy+2(xy)^2 x^5 +y^5 +xy(1−3xy)=1−4xy+2(xy)^2 x^5 +y^5 =1−5xy+5(xy)^2 (xy)^2 −xy=1−5xy+5(xy)^2 0=1−4xy+4(xy)^2 (2xy−1)^2 =0 ⇒xy=(1/2) x,y are roots of z^2 −z+(1/2)=0 z=(1/2)(1±i)=(1/( (√2)))((1/( (√2)))±(i/( (√2)))) =(1/( (√2)))[cos (±(π/4))+i sin (±(π/4))] z_1 ^(2022) =(1/2^(1011) )[cos (((2022π)/4))+i sin (((2022π)/4))] z_1 ^(2022) =(1/2^(1011) )[cos (505π+(π/2))+i sin (505π+(π/2))] z_1 ^(2022) =−(i/2^(1011) ) z_2 ^(2022) =(1/2^(1011) )[cos (−((2022π)/4))+i sin (−((2022π)/4))] z_2 ^(2022) =(1/2^(1011) )[cos (−505π−(π/2))+i sin (−505π−(π/2))] z_2 ^(2022) =(i/2^(1011) ) ⇒x^(2022) +y^(2022) =z_1 ^(2022) +z_2 ^(2022) =0 ⇒x^(2022) +xy+y^(2022) =(1/2) ✓

$${x}^{\mathrm{2}} +{y}^{\mathrm{2}} +\mathrm{2}{xy}=\mathrm{1} \\ $$$${x}^{\mathrm{2}} +{y}^{\mathrm{2}} =\mathrm{1}−\mathrm{2}{xy} \\ $$$$ \\ $$$$\left({x}^{\mathrm{2}} +{y}^{\mathrm{2}} \right)\left({x}+{y}\right)=\mathrm{1}−\mathrm{2}{xy} \\ $$$${x}^{\mathrm{3}} +{y}^{\mathrm{3}} +{xy}\left({x}+{y}\right)=\mathrm{1}−\mathrm{2}{xy} \\ $$$${x}^{\mathrm{3}} +{y}^{\mathrm{3}} =\mathrm{1}−\mathrm{3}{xy} \\ $$$$ \\ $$$${x}^{\mathrm{4}} +{y}^{\mathrm{4}} +\mathrm{2}\left({xy}\right)^{\mathrm{2}} =\mathrm{1}−\mathrm{4}{xy}+\mathrm{4}\left({xy}\right)^{\mathrm{2}} \\ $$$${x}^{\mathrm{4}} +{y}^{\mathrm{4}} =\mathrm{1}−\mathrm{4}{xy}+\mathrm{2}\left({xy}\right)^{\mathrm{2}} \\ $$$$ \\ $$$$\left({x}^{\mathrm{4}} +{y}^{\mathrm{4}} \right)\left({x}+{y}\right)=\mathrm{1}−\mathrm{4}{xy}+\mathrm{2}\left({xy}\right)^{\mathrm{2}} \\ $$$${x}^{\mathrm{5}} +{y}^{\mathrm{5}} +{xy}\left({x}^{\mathrm{3}} +{y}^{\mathrm{3}} \right)=\mathrm{1}−\mathrm{4}{xy}+\mathrm{2}\left({xy}\right)^{\mathrm{2}} \\ $$$${x}^{\mathrm{5}} +{y}^{\mathrm{5}} +{xy}\left(\mathrm{1}−\mathrm{3}{xy}\right)=\mathrm{1}−\mathrm{4}{xy}+\mathrm{2}\left({xy}\right)^{\mathrm{2}} \\ $$$${x}^{\mathrm{5}} +{y}^{\mathrm{5}} =\mathrm{1}−\mathrm{5}{xy}+\mathrm{5}\left({xy}\right)^{\mathrm{2}} \\ $$$$ \\ $$$$\left({xy}\right)^{\mathrm{2}} −{xy}=\mathrm{1}−\mathrm{5}{xy}+\mathrm{5}\left({xy}\right)^{\mathrm{2}} \\ $$$$\mathrm{0}=\mathrm{1}−\mathrm{4}{xy}+\mathrm{4}\left({xy}\right)^{\mathrm{2}} \\ $$$$\left(\mathrm{2}{xy}−\mathrm{1}\right)^{\mathrm{2}} =\mathrm{0} \\ $$$$\Rightarrow{xy}=\frac{\mathrm{1}}{\mathrm{2}} \\ $$$${x},{y}\:{are}\:{roots}\:{of} \\ $$$${z}^{\mathrm{2}} −{z}+\frac{\mathrm{1}}{\mathrm{2}}=\mathrm{0} \\ $$$${z}=\frac{\mathrm{1}}{\mathrm{2}}\left(\mathrm{1}\pm{i}\right)=\frac{\mathrm{1}}{\:\sqrt{\mathrm{2}}}\left(\frac{\mathrm{1}}{\:\sqrt{\mathrm{2}}}\pm\frac{{i}}{\:\sqrt{\mathrm{2}}}\right) \\ $$$$\:\:\:=\frac{\mathrm{1}}{\:\sqrt{\mathrm{2}}}\left[\mathrm{cos}\:\left(\pm\frac{\pi}{\mathrm{4}}\right)+{i}\:\mathrm{sin}\:\left(\pm\frac{\pi}{\mathrm{4}}\right)\right] \\ $$$$ \\ $$$${z}_{\mathrm{1}} ^{\mathrm{2022}} =\frac{\mathrm{1}}{\mathrm{2}^{\mathrm{1011}} }\left[\mathrm{cos}\:\left(\frac{\mathrm{2022}\pi}{\mathrm{4}}\right)+{i}\:\mathrm{sin}\:\left(\frac{\mathrm{2022}\pi}{\mathrm{4}}\right)\right] \\ $$$${z}_{\mathrm{1}} ^{\mathrm{2022}} =\frac{\mathrm{1}}{\mathrm{2}^{\mathrm{1011}} }\left[\mathrm{cos}\:\left(\mathrm{505}\pi+\frac{\pi}{\mathrm{2}}\right)+{i}\:\mathrm{sin}\:\left(\mathrm{505}\pi+\frac{\pi}{\mathrm{2}}\right)\right] \\ $$$${z}_{\mathrm{1}} ^{\mathrm{2022}} =−\frac{{i}}{\mathrm{2}^{\mathrm{1011}} } \\ $$$${z}_{\mathrm{2}} ^{\mathrm{2022}} =\frac{\mathrm{1}}{\mathrm{2}^{\mathrm{1011}} }\left[\mathrm{cos}\:\left(−\frac{\mathrm{2022}\pi}{\mathrm{4}}\right)+{i}\:\mathrm{sin}\:\left(−\frac{\mathrm{2022}\pi}{\mathrm{4}}\right)\right] \\ $$$${z}_{\mathrm{2}} ^{\mathrm{2022}} =\frac{\mathrm{1}}{\mathrm{2}^{\mathrm{1011}} }\left[\mathrm{cos}\:\left(−\mathrm{505}\pi−\frac{\pi}{\mathrm{2}}\right)+{i}\:\mathrm{sin}\:\left(−\mathrm{505}\pi−\frac{\pi}{\mathrm{2}}\right)\right] \\ $$$${z}_{\mathrm{2}} ^{\mathrm{2022}} =\frac{{i}}{\mathrm{2}^{\mathrm{1011}} } \\ $$$$\Rightarrow{x}^{\mathrm{2022}} +{y}^{\mathrm{2022}} ={z}_{\mathrm{1}} ^{\mathrm{2022}} +{z}_{\mathrm{2}} ^{\mathrm{2022}} =\mathrm{0} \\ $$$$\Rightarrow{x}^{\mathrm{2022}} +{xy}+{y}^{\mathrm{2022}} =\frac{\mathrm{1}}{\mathrm{2}}\:\checkmark \\ $$

Commented by behi834171 last updated on 23/Jul/22