Question Number 43539 by abdo.msup.com last updated on 11/Sep/18
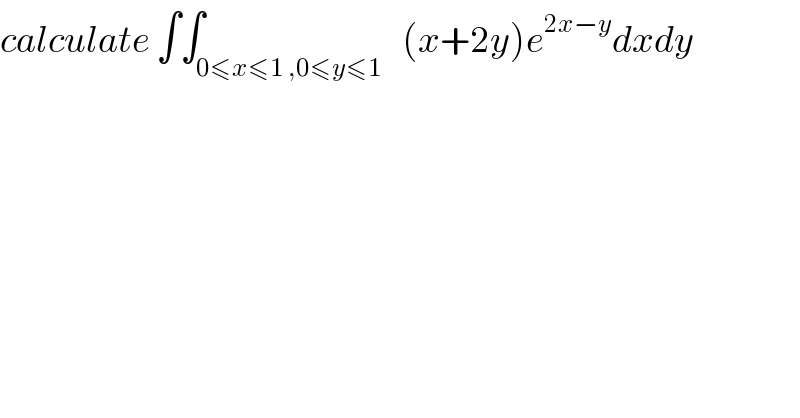
$${calculate}\:\int\int_{\mathrm{0}\leqslant{x}\leqslant\mathrm{1}\:,\mathrm{0}\leqslant{y}\leqslant\mathrm{1}} \:\:\left({x}+\mathrm{2}{y}\right){e}^{\mathrm{2}{x}−{y}} {dxdy} \\ $$
Commented by maxmathsup by imad last updated on 16/Sep/18
![let consider the diffeomorphisme (u,v) →ϕ(u,v)=(ϕ_1 (u,v),ϕ_2 (u,v))= (x,y) /u=x+2y and v=2x−y ⇒ { ((x+2y=u)),((2x−y=v ⇒ { ((2x+4y=2u)),((2x−y=v)) :})) :} ⇒ { ((5y=2u−v)),((x=u−2(((2u−v)/5)) ⇒ { ((y=(2/5)u−(1/5)v)),((x=(1/5)u +(2/5)v)) :})) :} ⇒ϕ(u,v)=(ϕ_1 ,ϕ_2 )=(x,y)=((1/5)u+(2/5)v,(2/5)u−(1/5)v)⇒ M_j (ϕ) = ((((∂ϕ_1 /∂u) (∂ϕ_1 /∂v))),(((∂ϕ_2 /∂u) (∂ϕ_2 /∂v))) ) = ((( (1/5) (2/5))),(((2/5) −(1/5))) ) and detM_j =−(1/(25)) −(4/(25)) =−(1/(25)) we have 0≤x≤1 and 0≤2y≤2 ⇒0≤x+2y≤3 ⇒0≤u≤3 0≤2x≤2 and −1≤−y≤0 ⇒−1≤2x−y≤ 2 ⇒−1≤v≤2 ⇒ ∫∫f(x,y)dxdy = ∫∫_w foϕ(u,v) ∣detM_j (ϕ)∣ du dv =∫∫_(0≤u≤3 and −1≤v≤2) u e^v (1/(25)) du dv =(1/(25)) ∫_0 ^3 udu .∫_(−1) ^2 e^v dv =(1/(25))[ (u^2 /2)]_0 ^3 .[ e^v ]_(−1) ^2 =(1/(50))(9)( e^2 −e^(−1) ) =(9/(50)){ e^2 −(1/e)} .](https://www.tinkutara.com/question/Q43849.png)
$${let}\:{consider}\:{the}\:{diffeomorphisme}\:\left({u},{v}\right)\:\rightarrow\varphi\left({u},{v}\right)=\left(\varphi_{\mathrm{1}} \left({u},{v}\right),\varphi_{\mathrm{2}} \left({u},{v}\right)\right)= \\ $$$$\left({x},{y}\right)\:/{u}={x}+\mathrm{2}{y}\:{and}\:{v}=\mathrm{2}{x}−{y}\:\Rightarrow\begin{cases}{{x}+\mathrm{2}{y}={u}}\\{\mathrm{2}{x}−{y}={v}\:\Rightarrow\begin{cases}{\mathrm{2}{x}+\mathrm{4}{y}=\mathrm{2}{u}}\\{\mathrm{2}{x}−{y}={v}}\end{cases}}\end{cases} \\ $$$$\Rightarrow\begin{cases}{\mathrm{5}{y}=\mathrm{2}{u}−{v}}\\{{x}={u}−\mathrm{2}\left(\frac{\mathrm{2}{u}−{v}}{\mathrm{5}}\right)\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\Rightarrow\:\:\begin{cases}{{y}=\frac{\mathrm{2}}{\mathrm{5}}{u}−\frac{\mathrm{1}}{\mathrm{5}}{v}}\\{{x}=\frac{\mathrm{1}}{\mathrm{5}}{u}\:+\frac{\mathrm{2}}{\mathrm{5}}{v}}\end{cases}}\end{cases} \\ $$$$\Rightarrow\varphi\left({u},{v}\right)=\left(\varphi_{\mathrm{1}} ,\varphi_{\mathrm{2}} \right)=\left({x},{y}\right)=\left(\frac{\mathrm{1}}{\mathrm{5}}{u}+\frac{\mathrm{2}}{\mathrm{5}}{v},\frac{\mathrm{2}}{\mathrm{5}}{u}−\frac{\mathrm{1}}{\mathrm{5}}{v}\right)\Rightarrow \\ $$$${M}_{{j}} \left(\varphi\right)\:=\begin{pmatrix}{\frac{\partial\varphi_{\mathrm{1}} }{\partial{u}}\:\:\:\:\:\:\:\:\:\:\:\:\:\:\frac{\partial\varphi_{\mathrm{1}} }{\partial{v}}}\\{\frac{\partial\varphi_{\mathrm{2}} }{\partial{u}}\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\frac{\partial\varphi_{\mathrm{2}} }{\partial{v}}}\end{pmatrix}\:\:\:\:\:\:\:=\:\begin{pmatrix}{\:\frac{\mathrm{1}}{\mathrm{5}}\:\:\:\:\:\:\:\:\:\frac{\mathrm{2}}{\mathrm{5}}}\\{\frac{\mathrm{2}}{\mathrm{5}}\:\:\:\:\:\:\:\:\:−\frac{\mathrm{1}}{\mathrm{5}}}\end{pmatrix}\:\:{and}\:{detM}_{{j}} =−\frac{\mathrm{1}}{\mathrm{25}}\:−\frac{\mathrm{4}}{\mathrm{25}}\:=−\frac{\mathrm{1}}{\mathrm{25}} \\ $$$${we}\:{have}\:\mathrm{0}\leqslant{x}\leqslant\mathrm{1}\:{and}\:\mathrm{0}\leqslant\mathrm{2}{y}\leqslant\mathrm{2}\:\Rightarrow\mathrm{0}\leqslant{x}+\mathrm{2}{y}\leqslant\mathrm{3}\:\Rightarrow\mathrm{0}\leqslant{u}\leqslant\mathrm{3}\: \\ $$$$\mathrm{0}\leqslant\mathrm{2}{x}\leqslant\mathrm{2}\:{and}\:\:−\mathrm{1}\leqslant−{y}\leqslant\mathrm{0}\:\Rightarrow−\mathrm{1}\leqslant\mathrm{2}{x}−{y}\leqslant\:\mathrm{2}\:\Rightarrow−\mathrm{1}\leqslant{v}\leqslant\mathrm{2}\:\Rightarrow \\ $$$$\int\int{f}\left({x},{y}\right){dxdy}\:\:=\:\int\int_{{w}} {fo}\varphi\left({u},{v}\right)\:\mid{detM}_{{j}} \left(\varphi\right)\mid\:{du}\:{dv} \\ $$$$=\int\int_{\mathrm{0}\leqslant{u}\leqslant\mathrm{3}\:{and}\:−\mathrm{1}\leqslant{v}\leqslant\mathrm{2}} \:{u}\:{e}^{{v}} \:\frac{\mathrm{1}}{\mathrm{25}}\:{du}\:{dv}\:=\frac{\mathrm{1}}{\mathrm{25}}\:\int_{\mathrm{0}} ^{\mathrm{3}} \:{udu}\:\:.\int_{−\mathrm{1}} ^{\mathrm{2}} \:{e}^{{v}} {dv} \\ $$$$=\frac{\mathrm{1}}{\mathrm{25}}\left[\:\frac{{u}^{\mathrm{2}} }{\mathrm{2}}\right]_{\mathrm{0}} ^{\mathrm{3}} \:.\left[\:{e}^{{v}} \right]_{−\mathrm{1}} ^{\mathrm{2}} \:\:=\frac{\mathrm{1}}{\mathrm{50}}\left(\mathrm{9}\right)\left(\:{e}^{\mathrm{2}} \:−{e}^{−\mathrm{1}} \right)\:=\frac{\mathrm{9}}{\mathrm{50}}\left\{\:{e}^{\mathrm{2}} \:−\frac{\mathrm{1}}{{e}}\right\}\:. \\ $$
