Question Number 43935 by abdo.msup.com last updated on 18/Sep/18
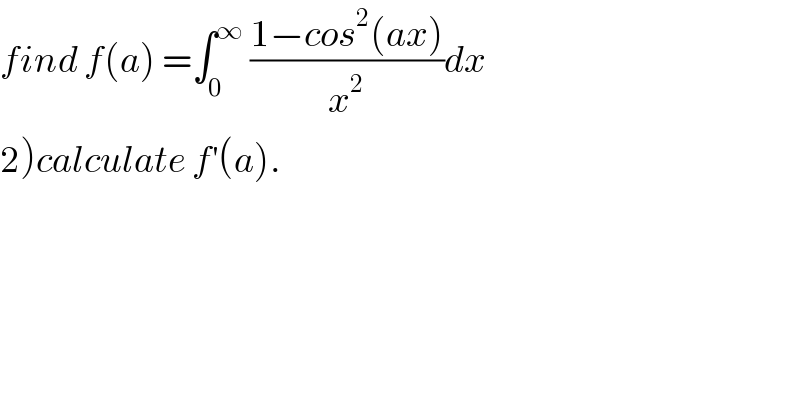
$${find}\:{f}\left({a}\right)\:=\int_{\mathrm{0}} ^{\infty} \:\frac{\mathrm{1}−{cos}^{\mathrm{2}} \left({ax}\right)}{{x}^{\mathrm{2}} }{dx} \\ $$$$\left.\mathrm{2}\right){calculate}\:{f}^{'} \left({a}\right). \\ $$
Commented by maxmathsup by imad last updated on 19/Sep/18
![we have f(a) = ∫_0 ^∞ ((sin^2 (ax))/x^2 )dx =_(ax=t) ∫_0 ^∞ ((sin^2 t)/(((t/a))^2 )) (dt/a) = a ∫_0 ^∞ ((sin^2 t)/t^2 )dt by parts u^′ =(1/t^2 ) and v=sin^2 t ⇒ f(a) =a { [−(1/t) sin^2 t]_0 ^∞ −∫_0 ^∞ −(1/t) (2sint cost)dt} =a{ 2 ∫_0 ^∞ ((sint cost)/t)dt} =a ∫_0 ^∞ ((sin(2t))/t)dt =_(2t =u) a ∫_0 ^∞ ((sin(u))/(u/2)) (du/2) = a ∫_0 ^∞ ((sin(u))/u) du =a (π/2) ⇒f(a) =((πa)/2) . 2) we have f(a) =((πa)/2) ⇒f^′ (a) =0 .](https://www.tinkutara.com/question/Q44008.png)
$${we}\:{have}\:{f}\left({a}\right)\:=\:\int_{\mathrm{0}} ^{\infty} \:\:\:\frac{{sin}^{\mathrm{2}} \left({ax}\right)}{{x}^{\mathrm{2}} }{dx}\:=_{{ax}={t}} \:\:\int_{\mathrm{0}} ^{\infty} \:\:\:\frac{{sin}^{\mathrm{2}} {t}}{\left(\frac{{t}}{{a}}\right)^{\mathrm{2}} }\:\frac{{dt}}{{a}} \\ $$$$=\:{a}\:\int_{\mathrm{0}} ^{\infty} \:\:\frac{{sin}^{\mathrm{2}} {t}}{{t}^{\mathrm{2}} }{dt}\:\:\:{by}\:{parts}\:\:{u}^{'} =\frac{\mathrm{1}}{{t}^{\mathrm{2}} }\:{and}\:{v}={sin}^{\mathrm{2}} {t}\:\Rightarrow \\ $$$${f}\left({a}\right)\:={a}\:\left\{\:\left[−\frac{\mathrm{1}}{{t}}\:{sin}^{\mathrm{2}} {t}\right]_{\mathrm{0}} ^{\infty} \:−\int_{\mathrm{0}} ^{\infty} \:\:\:−\frac{\mathrm{1}}{{t}}\:\left(\mathrm{2}{sint}\:{cost}\right){dt}\right\} \\ $$$$={a}\left\{\:\:\mathrm{2}\:\int_{\mathrm{0}} ^{\infty} \:\:\frac{{sint}\:{cost}}{{t}}{dt}\right\}\:={a}\:\int_{\mathrm{0}} ^{\infty} \:\:\:\frac{{sin}\left(\mathrm{2}{t}\right)}{{t}}{dt}\:\:=_{\mathrm{2}{t}\:={u}} \:\:\:{a}\:\int_{\mathrm{0}} ^{\infty} \:\:\:\frac{{sin}\left({u}\right)}{\frac{{u}}{\mathrm{2}}}\:\frac{{du}}{\mathrm{2}} \\ $$$$=\:{a}\:\int_{\mathrm{0}} ^{\infty} \:\:\:\frac{{sin}\left({u}\right)}{{u}}\:{du}\:={a}\:\frac{\pi}{\mathrm{2}}\:\:\Rightarrow{f}\left({a}\right)\:=\frac{\pi{a}}{\mathrm{2}}\:. \\ $$$$\left.\mathrm{2}\right)\:{we}\:{have}\:{f}\left({a}\right)\:=\frac{\pi{a}}{\mathrm{2}}\:\Rightarrow{f}^{'} \left({a}\right)\:=\mathrm{0}\:. \\ $$
