Question Number 109913 by mohammad17 last updated on 26/Aug/20
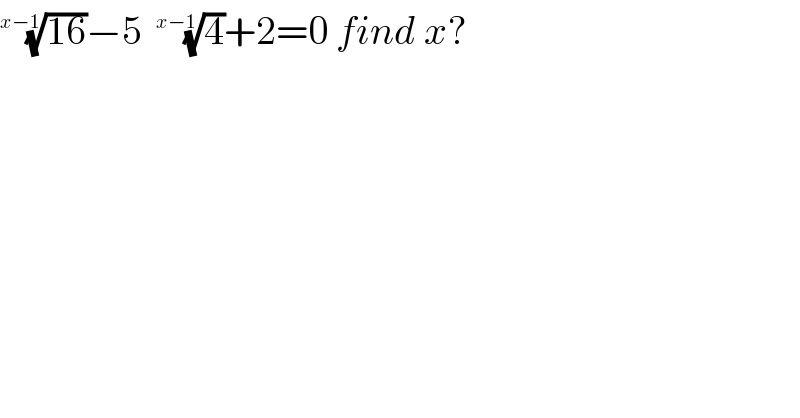
$$\sqrt[{{x}−\mathrm{1}}]{\mathrm{16}}−\mathrm{5}\:\:\sqrt[{{x}−\mathrm{1}}]{\mathrm{4}}+\mathrm{2}=\mathrm{0}\:{find}\:{x}? \\ $$
Answered by Rasheed.Sindhi last updated on 26/Aug/20
![((16))^(1/(x−1)) −5 (4)^(1/(x−1)) +2=0 find x? 16^(1/(x−1)) −5(4)^(1/(x−1)) +2=0 (4^(1/(x−1)) )^2 −5(4^(1/(x−1)) )+2=0 y^2 −5y+2=0; [ 4^(1/(x−1)) =y] y=((5±(√(25−8)))/2)=((5±(√(17)))/2) 4^(1/(x−1)) =((5±(√(17)))/2) ((1/(x−1)))log_2 4=log_2 (((5±(√(17)))/2)) ((1/(x−1)))log_2 4=log_2 (((5±(√(17)))/2)) 2((1/(x−1)))=log_2 (((5±(√(17)))/2)) x=(2/(log_2 (((5±(√(17)))/2))))+1](https://www.tinkutara.com/question/Q109915.png)
$$\sqrt[{{x}−\mathrm{1}}]{\mathrm{16}}−\mathrm{5}\:\:\sqrt[{{x}−\mathrm{1}}]{\mathrm{4}}+\mathrm{2}=\mathrm{0}\:{find}\:{x}? \\ $$$$\mathrm{16}^{\frac{\mathrm{1}}{{x}−\mathrm{1}}} −\mathrm{5}\left(\mathrm{4}\right)^{\frac{\mathrm{1}}{{x}−\mathrm{1}}} +\mathrm{2}=\mathrm{0} \\ $$$$\left(\mathrm{4}^{\frac{\mathrm{1}}{{x}−\mathrm{1}}} \right)^{\mathrm{2}} −\mathrm{5}\left(\mathrm{4}^{\frac{\mathrm{1}}{{x}−\mathrm{1}}} \right)+\mathrm{2}=\mathrm{0} \\ $$$${y}^{\mathrm{2}} −\mathrm{5}{y}+\mathrm{2}=\mathrm{0};\:\left[\:\mathrm{4}^{\frac{\mathrm{1}}{{x}−\mathrm{1}}} ={y}\right] \\ $$$${y}=\frac{\mathrm{5}\pm\sqrt{\mathrm{25}−\mathrm{8}}}{\mathrm{2}}=\frac{\mathrm{5}\pm\sqrt{\mathrm{17}}}{\mathrm{2}} \\ $$$$\mathrm{4}^{\frac{\mathrm{1}}{{x}−\mathrm{1}}} =\frac{\mathrm{5}\pm\sqrt{\mathrm{17}}}{\mathrm{2}} \\ $$$$\left(\frac{\mathrm{1}}{{x}−\mathrm{1}}\right)\mathrm{log}_{\mathrm{2}} \mathrm{4}=\mathrm{log}_{\mathrm{2}} \left(\frac{\mathrm{5}\pm\sqrt{\mathrm{17}}}{\mathrm{2}}\right) \\ $$$$\left(\frac{\mathrm{1}}{{x}−\mathrm{1}}\right)\mathrm{log}_{\mathrm{2}} \mathrm{4}=\mathrm{log}_{\mathrm{2}} \left(\frac{\mathrm{5}\pm\sqrt{\mathrm{17}}}{\mathrm{2}}\right) \\ $$$$\mathrm{2}\left(\frac{\mathrm{1}}{{x}−\mathrm{1}}\right)=\mathrm{log}_{\mathrm{2}} \left(\frac{\mathrm{5}\pm\sqrt{\mathrm{17}}}{\mathrm{2}}\right) \\ $$$$\:\:\:{x}=\frac{\mathrm{2}}{\mathrm{log}_{\mathrm{2}} \left(\frac{\mathrm{5}\pm\sqrt{\mathrm{17}}}{\mathrm{2}}\right)}+\mathrm{1} \\ $$
Commented by mohammad17 last updated on 26/Aug/20

$$ \\ $$$$={thank}\:{you}\:{sir} \\ $$
