0-pi-2-dx-1-tan-13-x-

Question Number 45021 by rahul 19 last updated on 07/Oct/18

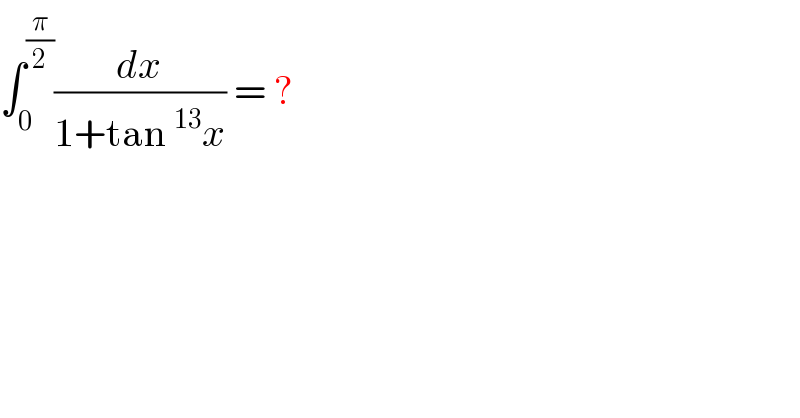
$$\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \frac{{dx}}{\mathrm{1}+\mathrm{tan}\:^{\mathrm{13}} {x}}\:=\:? \\ $$

Answered by tanmay.chaudhury50@gmail.com last updated on 07/Oct/18

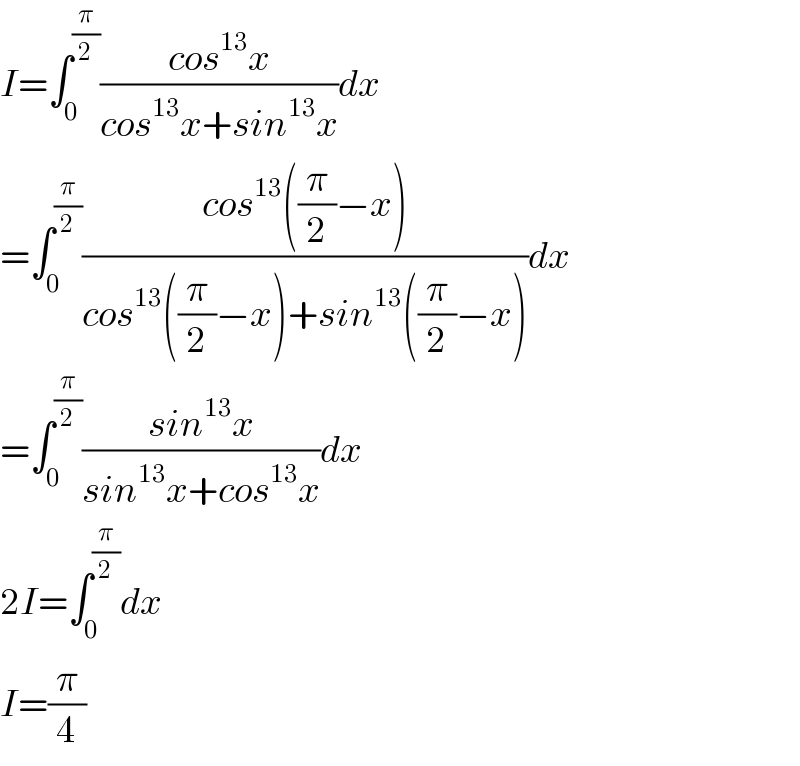
$${I}=\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \frac{{cos}^{\mathrm{13}} {x}}{{cos}^{\mathrm{13}} {x}+{sin}^{\mathrm{13}} {x}}{dx} \\ $$$$=\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \frac{{cos}^{\mathrm{13}} \left(\frac{\pi}{\mathrm{2}}−{x}\right)}{{cos}^{\mathrm{13}} \left(\frac{\pi}{\mathrm{2}}−{x}\right)+{sin}^{\mathrm{13}} \left(\frac{\pi}{\mathrm{2}}−{x}\right)}{dx} \\ $$$$=\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \frac{{sin}^{\mathrm{13}} {x}}{{sin}^{\mathrm{13}} {x}+{cos}^{\mathrm{13}} {x}}{dx} \\ $$$$\mathrm{2}{I}=\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} {dx} \\ $$$${I}=\frac{\pi}{\mathrm{4}} \\ $$

Commented by rahul 19 last updated on 07/Oct/18

thanks sir ��

Commented by malwaan last updated on 14/Oct/18

$$\mathrm{great} \\ $$

Answered by math1967 last updated on 07/Oct/18

$${I}=\underset{\mathrm{0}} {\overset{\frac{\pi}{\mathrm{2}}} {\int}}\frac{{dx}}{\mathrm{1}+{tan}^{\mathrm{13}} \left(\frac{\pi}{\mathrm{2}}−{x}\right)}=\underset{\mathrm{0}} {\overset{\frac{\pi}{\mathrm{2}}} {\int}}\frac{{dx}}{\mathrm{1}+{cot}^{\mathrm{13}} {x}} \\ $$$$=\underset{\mathrm{0}} {\overset{\frac{\pi}{\mathrm{2}}} {\int}}\frac{{dx}}{\mathrm{1}+\frac{\mathrm{1}}{{tan}^{\mathrm{13}} {x}}}=\underset{\mathrm{0}} {\overset{\frac{\pi}{\mathrm{2}}} {\int}}\frac{{tan}^{\mathrm{13}} {x}}{\mathrm{1}+{tan}^{\mathrm{13}} {x}}{dx} \\ $$$$\therefore\mathrm{2}{I}=\underset{\mathrm{0}} {\overset{\frac{\pi}{\mathrm{2}}} {\int}}\frac{\mathrm{1}+{tan}^{\mathrm{13}} {x}}{\mathrm{1}+{tan}^{\mathrm{13}} {x}}{dx}=\left[{x}\right]_{\mathrm{0}\:\:} ^{\frac{\pi}{\mathrm{2}}} =\frac{\pi}{\mathrm{2}} \\ $$$${I}=\frac{\pi}{\mathrm{4}}\:{ans}. \\ $$

Commented by rahul 19 last updated on 07/Oct/18

thanks sir ��

Terms of Service
Privacy Policy
Contact: info@tinkutara.com