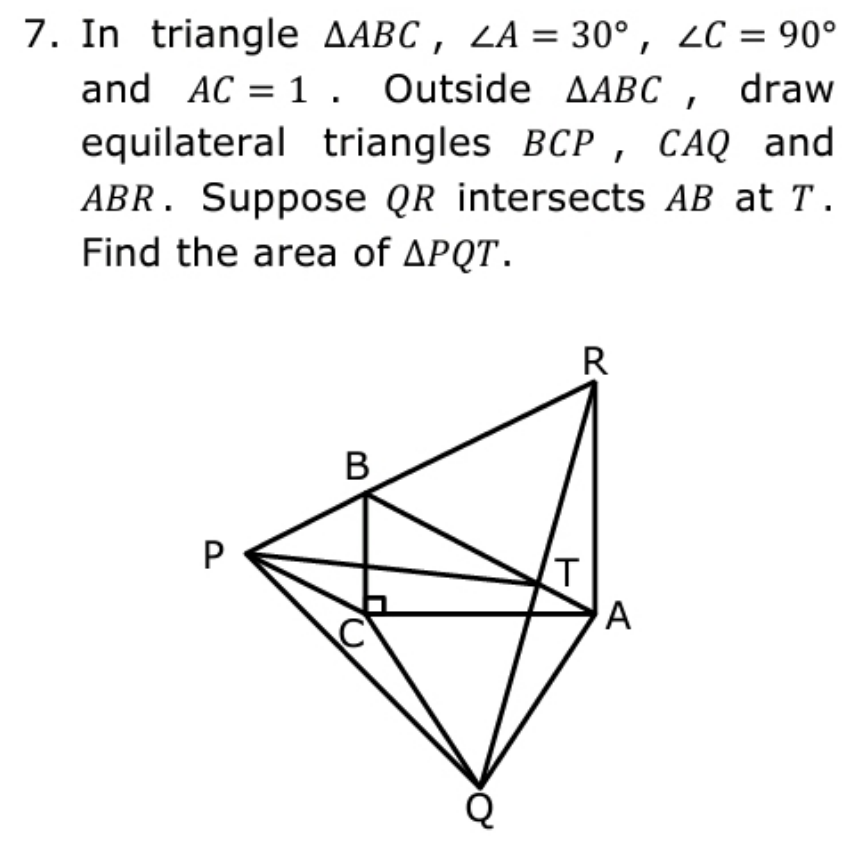
Question Number 176195 by adhigenz last updated on 14/Sep/22
Answered by behi834171 last updated on 15/Sep/22
![BC=BP=PC=((√3)/3),AB=AR=BR=((2(√3))/3) PQ^2 =(1/3)+1−2×((√3)/3)×1×cos(150)= =(1/3)+1+2×((√3)/3)×((√3)/2)⇒PQ=(√(7/3)) cos∡CPQ=(((((√3)/3))^2 +((√(7/3)))^2 −1^2 )/(2((√3)/3).(√(7/3))))=(5/(2(√7))) ⇒∡CPQ=19.12^• RQ^2 =PR^2 +PQ^2 −2PR.PQ.cos(60+19.12)= =((√3))^2 +((√(7/3)))^2 −2×(√3)×(√(7/3)).[(1/2).(5/(2(√7)))−((√3)/2).((√3)/(2(√7)))]= =3+(7/3)−1=((13)/3)⇒RQ=(√((13)/3)) cosAQT=((((√((13)/3)))^2 +1^2 −(2((√3)/3))^2 )/(2×((√(13))/( (√3)))×1))=((((13)/3)+1−(4/3))/((2(√(13)))/( (√3))))= =(((12)/3)/((2(√(13)))/( (√3))))=(6/( (√(39)))) TQ=(1/(cosAQT))=((√(39))/6) TR=QR−QT=(√((13)/3))−((√(39))/6)=((√(39))/3) QR(PT^2 +QT.TR)=PR^2 .QT+PQ^2 .TR⇒ (√((13)/3))(PT^2 +((√(39))/6).((√(39))/( 3)))=((√3))^2 .((√(39))/6)+((√(7/3)))^2 .((√(39))/3)⇒ ⇒(√((13)/3))(PT^2 +((39)/(18)))=((√(39))/2)+((7(√(39)))/9)=((23(√(39)))/(18)) ⇒PT^2 =((23(√(39)))/(18))×((√3)/( (√(13))))−((39)/(18))=((30)/(18))=(5/3) ⇒PT=(√(5/3)) now: PT=(√(5/3))=((√(15))/3),TQ=((√(39))/6),PQ=(√(7/3))=((√(21))/3) PT=1.29,TQ=1.04,PQ=1.53 p=((1.29+1.04+1.53)/2)=1.93 Area=(√(1.93×0.64×0.89×0.40))=0.66 .■ [area=((√(1015))/(48))]](https://www.tinkutara.com/question/Q176198.png)
$${BC}={BP}={PC}=\frac{\sqrt{\mathrm{3}}}{\mathrm{3}},{AB}={AR}={BR}=\frac{\mathrm{2}\sqrt{\mathrm{3}}}{\mathrm{3}} \\ $$$${PQ}^{\mathrm{2}} =\frac{\mathrm{1}}{\mathrm{3}}+\mathrm{1}−\mathrm{2}×\frac{\sqrt{\mathrm{3}}}{\mathrm{3}}×\mathrm{1}×{cos}\left(\mathrm{150}\right)= \\ $$$$=\frac{\mathrm{1}}{\mathrm{3}}+\mathrm{1}+\mathrm{2}×\frac{\sqrt{\mathrm{3}}}{\mathrm{3}}×\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}\Rightarrow{PQ}=\sqrt{\frac{\mathrm{7}}{\mathrm{3}}} \\ $$$${cos}\measuredangle{CPQ}=\frac{\left(\frac{\sqrt{\mathrm{3}}}{\mathrm{3}}\right)^{\mathrm{2}} +\left(\sqrt{\frac{\mathrm{7}}{\mathrm{3}}}\right)^{\mathrm{2}} −\mathrm{1}^{\mathrm{2}} }{\mathrm{2}\frac{\sqrt{\mathrm{3}}}{\mathrm{3}}.\sqrt{\frac{\mathrm{7}}{\mathrm{3}}}}=\frac{\mathrm{5}}{\mathrm{2}\sqrt{\mathrm{7}}} \\ $$$$\Rightarrow\measuredangle{CPQ}=\mathrm{19}.\mathrm{12}^{\bullet} \\ $$$${RQ}^{\mathrm{2}} ={PR}^{\mathrm{2}} +{PQ}^{\mathrm{2}} −\mathrm{2}{PR}.{PQ}.{cos}\left(\mathrm{60}+\mathrm{19}.\mathrm{12}\right)= \\ $$$$=\left(\sqrt{\mathrm{3}}\right)^{\mathrm{2}} +\left(\sqrt{\frac{\mathrm{7}}{\mathrm{3}}}\right)^{\mathrm{2}} −\mathrm{2}×\sqrt{\mathrm{3}}×\sqrt{\frac{\mathrm{7}}{\mathrm{3}}}.\left[\frac{\mathrm{1}}{\mathrm{2}}.\frac{\mathrm{5}}{\mathrm{2}\sqrt{\mathrm{7}}}−\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}.\frac{\sqrt{\mathrm{3}}}{\mathrm{2}\sqrt{\mathrm{7}}}\right]= \\ $$$$=\mathrm{3}+\frac{\mathrm{7}}{\mathrm{3}}−\mathrm{1}=\frac{\mathrm{13}}{\mathrm{3}}\Rightarrow\boldsymbol{{RQ}}=\sqrt{\frac{\mathrm{13}}{\mathrm{3}}} \\ $$$$\boldsymbol{{cosAQT}}=\frac{\left(\sqrt{\frac{\mathrm{13}}{\mathrm{3}}}\right)^{\mathrm{2}} +\mathrm{1}^{\mathrm{2}} −\left(\mathrm{2}\frac{\sqrt{\mathrm{3}}}{\mathrm{3}}\right)^{\mathrm{2}} }{\mathrm{2}×\frac{\sqrt{\mathrm{13}}}{\:\sqrt{\mathrm{3}}}×\mathrm{1}}=\frac{\frac{\mathrm{13}}{\mathrm{3}}+\mathrm{1}−\frac{\mathrm{4}}{\mathrm{3}}}{\frac{\mathrm{2}\sqrt{\mathrm{13}}}{\:\sqrt{\mathrm{3}}}}= \\ $$$$=\frac{\frac{\mathrm{12}}{\mathrm{3}}}{\frac{\mathrm{2}\sqrt{\mathrm{13}}}{\:\sqrt{\mathrm{3}}}}=\frac{\mathrm{6}}{\:\sqrt{\mathrm{39}}} \\ $$$${TQ}=\frac{\mathrm{1}}{\boldsymbol{{cos}}{AQT}}=\frac{\sqrt{\mathrm{39}}}{\mathrm{6}} \\ $$$${TR}={QR}−{QT}=\sqrt{\frac{\mathrm{13}}{\mathrm{3}}}−\frac{\sqrt{\mathrm{39}}}{\mathrm{6}}=\frac{\sqrt{\mathrm{39}}}{\mathrm{3}} \\ $$$${QR}\left({PT}^{\mathrm{2}} +{QT}.{TR}\right)={PR}^{\mathrm{2}} .{QT}+{PQ}^{\mathrm{2}} .{TR}\Rightarrow \\ $$$$\sqrt{\frac{\mathrm{13}}{\mathrm{3}}}\left({PT}^{\mathrm{2}} +\frac{\sqrt{\mathrm{39}}}{\mathrm{6}}.\frac{\sqrt{\mathrm{39}}}{\:\mathrm{3}}\right)=\left(\sqrt{\mathrm{3}}\right)^{\mathrm{2}} .\frac{\sqrt{\mathrm{39}}}{\mathrm{6}}+\left(\sqrt{\frac{\mathrm{7}}{\mathrm{3}}}\right)^{\mathrm{2}} .\frac{\sqrt{\mathrm{39}}}{\mathrm{3}}\Rightarrow \\ $$$$\Rightarrow\sqrt{\frac{\mathrm{13}}{\mathrm{3}}}\left({PT}^{\mathrm{2}} +\frac{\mathrm{39}}{\mathrm{18}}\right)=\frac{\sqrt{\mathrm{39}}}{\mathrm{2}}+\frac{\mathrm{7}\sqrt{\mathrm{39}}}{\mathrm{9}}=\frac{\mathrm{23}\sqrt{\mathrm{39}}}{\mathrm{18}} \\ $$$$\Rightarrow{PT}^{\mathrm{2}} =\frac{\mathrm{23}\sqrt{\mathrm{39}}}{\mathrm{18}}×\frac{\sqrt{\mathrm{3}}}{\:\sqrt{\mathrm{13}}}−\frac{\mathrm{39}}{\mathrm{18}}=\frac{\mathrm{30}}{\mathrm{18}}=\frac{\mathrm{5}}{\mathrm{3}} \\ $$$$\Rightarrow\boldsymbol{{PT}}=\sqrt{\frac{\mathrm{5}}{\mathrm{3}}} \\ $$$$\boldsymbol{{now}}: \\ $$$$\boldsymbol{{PT}}=\sqrt{\frac{\mathrm{5}}{\mathrm{3}}}=\frac{\sqrt{\mathrm{15}}}{\mathrm{3}},\boldsymbol{{TQ}}=\frac{\sqrt{\mathrm{39}}}{\mathrm{6}},\boldsymbol{{PQ}}=\sqrt{\frac{\mathrm{7}}{\mathrm{3}}}=\frac{\sqrt{\mathrm{21}}}{\mathrm{3}} \\ $$$$\boldsymbol{{PT}}=\mathrm{1}.\mathrm{29},\boldsymbol{{TQ}}=\mathrm{1}.\mathrm{04},\boldsymbol{{PQ}}=\mathrm{1}.\mathrm{53} \\ $$$$\boldsymbol{{p}}=\frac{\mathrm{1}.\mathrm{29}+\mathrm{1}.\mathrm{04}+\mathrm{1}.\mathrm{53}}{\mathrm{2}}=\mathrm{1}.\mathrm{93} \\ $$$$\boldsymbol{{A}}{rea}=\sqrt{\mathrm{1}.\mathrm{93}×\mathrm{0}.\mathrm{64}×\mathrm{0}.\mathrm{89}×\mathrm{0}.\mathrm{40}}=\mathrm{0}.\mathrm{66}\:\:\:.\blacksquare \\ $$$$\left[\boldsymbol{{area}}=\frac{\sqrt{\mathrm{1015}}}{\mathrm{48}}\right] \\ $$
Commented by adhigenz last updated on 15/Sep/22
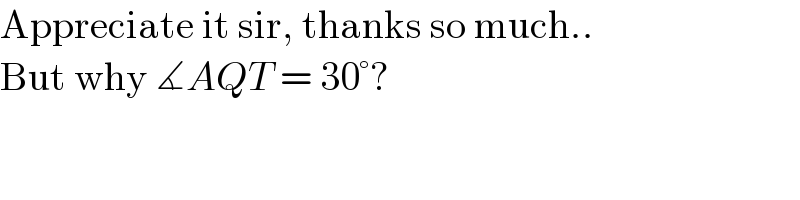
$$\mathrm{Appreciate}\:\mathrm{it}\:\mathrm{sir},\:\mathrm{thanks}\:\mathrm{so}\:\mathrm{much}.. \\ $$$$\mathrm{But}\:\mathrm{why}\:\measuredangle{AQT}\:=\:\mathrm{30}°? \\ $$
Commented by adhigenz last updated on 15/Sep/22
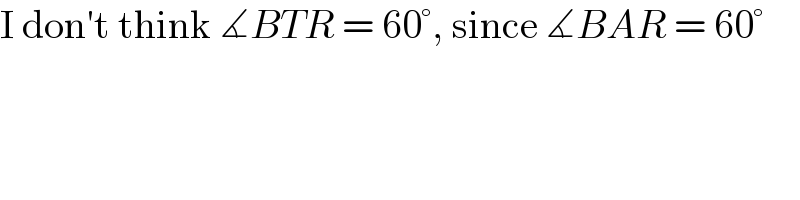
$$\mathrm{I}\:\mathrm{don}'\mathrm{t}\:\mathrm{think}\:\measuredangle{BTR}\:=\:\mathrm{60}°,\:\mathrm{since}\:\measuredangle{BAR}\:=\:\mathrm{60}° \\ $$
Commented by Tawa11 last updated on 15/Sep/22

$$\mathrm{Great}\:\mathrm{sir}. \\ $$
Commented by behi834171 last updated on 15/Sep/22
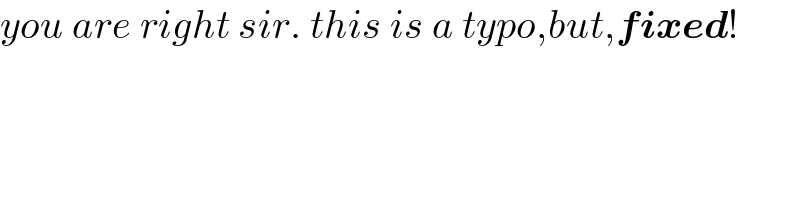
$${you}\:{are}\:{right}\:{sir}.\:{this}\:{is}\:{a}\:{typo},{but},\boldsymbol{{fixed}}! \\ $$
